Réseau(x) routier(s) aléatoire(s)

Autour du sujet de TIPE de @mathieu_bory

Modélisations

• Par des graphes

plt.figure()
plt.plot([1,4,2,0,3,7],[4,3,1,0,-1,-1],'ko')
plt.plot([1,4],[4,3],'k:')
plt.plot([3,2,7],[-1,1,-1],'k:')
textes = [(1,4.1,'$P_0$'),(4,3.1,'$P_1$'),(2,1.1,'$P_2$'),(0,0.1,'$P_3$'),
          (3,-0.9,'$P_4$'),(7,-0.9,'$P_5$'),(2.5,3.6,'$A_0$'),(2.6,0.1,'$A_1$'),
          (4.6,0.1,'$A_2$')]
for a,b,c in textes:
    plt.text(a,b,c)

Modélisations

• Par des graphes

Sommets = [(1,4,'P0'),(4,3,'P1'),(2,1,'P2'),(0,0,'P3'),
          (3,-1,'P4'),(7,-1,'P5')]
Aretes = [(0,1),(2,4),(2,5)]

Modélisations

• Par un tableau numpy ou une liste de listes

import numpy as np
depart = [[0,0,0,0,0],[0,1,0,1,0],[0,0,0,0,0],[0,1,0,1,0],[0,0,0,0,0]]
plt.figure()
plt.imshow(depart)

<matplotlib.image.AxesImage at 0x1a63bf1ce88>

def depart(n):
    result = np.zeros((2*n+1,2*n+1), dtype=int)
    result[1::2, 1::2] = 1
    return result
plt.figure()
plt.imshow(depart(5))

<matplotlib.image.AxesImage at 0x1a63bf6c408>

Fabrication du labyrinthe

from IPython.display import HTML
HTML("""<video width="520" height="520" controls> <source src="construction.mp4" type="video/mp4"> </video>""")

HTML("""<video width="600" height="600" controls> <source src="construction2.mp4" type="video/mp4"> </video>""")

Quelques propriétés d'un labyrinthe

• Si dans la situation de départ, on met $n\times n$ cellules vides dans le tableau numpy, le reste du tableau étant rempli de murs, alors la taille du tableau est...

$$(2n+1)\times(2n+1)=4n^2+4n+1$$

• À la fin de l'algorithme, combien de murs auront été abattus ?
  1. On ne peut pas savoir mais on peut fixer une borne supérieure ?
  2. On ne peut pas savoir mais on peut fixer une borne inférieure ?
  3. On peut savoir d'ailleurs je sais :-)

À la fin de l'algorithme, par constrction, $n^2-1$ murs exactement auront été abattus : en effet,

Une petite démonstration :-)

Chaque étape de l'algorithme détruit un mur entre deux composantes connexes distinctes.

Donc à chaque étape de l'algorithme, le nombre de composantes connexes diminue de 1.

Or, au départ de l'algorithme il y a $n^2$ composantes connexes, et à la fin de l'algorithme il n'y en a plus qu'une.

Donc l'algorithme comprend $n^2-1$ étapes, détruisant chacune un mur, et faisant apparaître à la place une cellule vide...

Quelques propriétés d'un labyrinthe

• Si dans la situation de départ, on met $n\times n$ cellules vides dans le tableau numpy, le reste du tableau étant rempli de murs, alors la taille du tableau est $$(2n+1)\times(2n+1)=4n^2+4n+1$$
• À la fin de l'algorithme, $n^2-1$ murs auront été détruits.
• Combien de cellules (vides) forment le labyrinthe final ?

$$n^2+n^2-1=2n^2-1$$

• Combien de murs restent intacts dans le tableau numpy à la fin de l'algorithme ?

$$4n^2+4n+1-\left(2n^2-1\right)=2n^2+4n+2=2\left(n+1\right)^2$$

Notamment, un labyrinthe, une fois construit, comprend asymptotiquement autant de cases vides que de murs.

Quelques propriétés d'un labyrinthe

Entre deux cases quelconques du labyrinthe (final), il y a un chemin et un seul.

Remarque :

Il faut s'entendre sur ce qu'on appelle chemin :

• Un chemin entre deux points $A$ et $B$ est une famille injective de points adjacents dont le premier point est $A$ et le dernier est $B$...
• Autrement dit, on n'autorise pas un chemin à passer plusieurs fois par une même case.

Quelques propriétés d'un labyrinthe

Entre deux cases quelconques du labyrinthe (final), il y a un chemin et un seul.

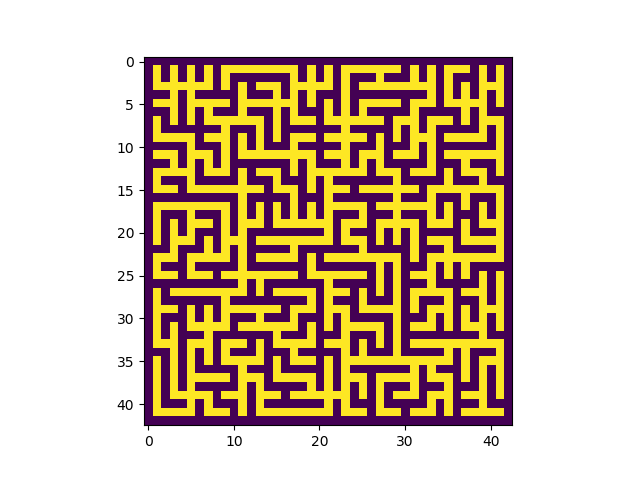
Quelques propriétés d'un labyrinthe

Entre deux cases quelconques du labyrinthe (final), il y a un chemin et un seul.

Quelques propriétés d'un labyrinthe

Entre deux cases quelconques du labyrinthe (final), il y a un chemin et un seul.

Démonstration

C'est une propriété initialisée :

Quelques propriétés d'un labyrinthe

Entre deux cases quelconques du labyrinthe (final), il y a un chemin et un seul.

Démonstration

C'est une propriété héréditaire :

HTML("""<video width="500" height="500" controls> <source src="heredite.mp4" type="video/mp4"> </video>""")

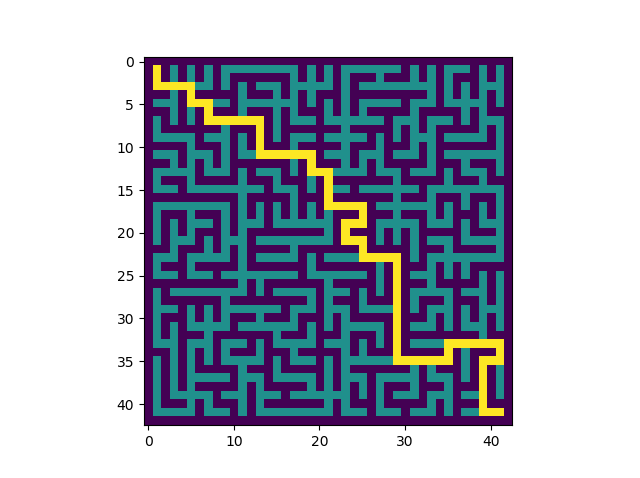
Quelques propriétés d'un labyrinthe

Entre deux cases quelconques du labyrinthe (final), il y a un chemin et un seul.

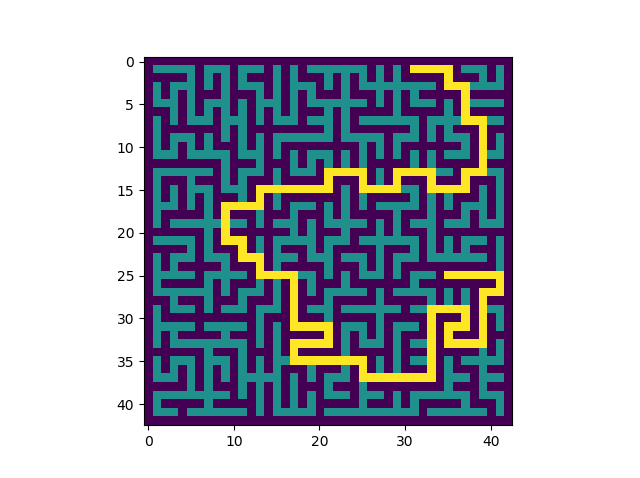
Celui-ci est de longueur 125. Mais ce n'est pas le plus long de son labyrinthe.

Visualiser les distances...

Voici le plus long de ce labyrinthe (longueur 153) :

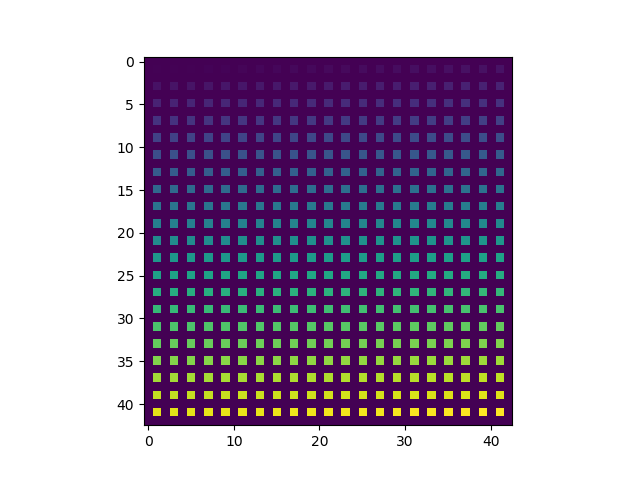
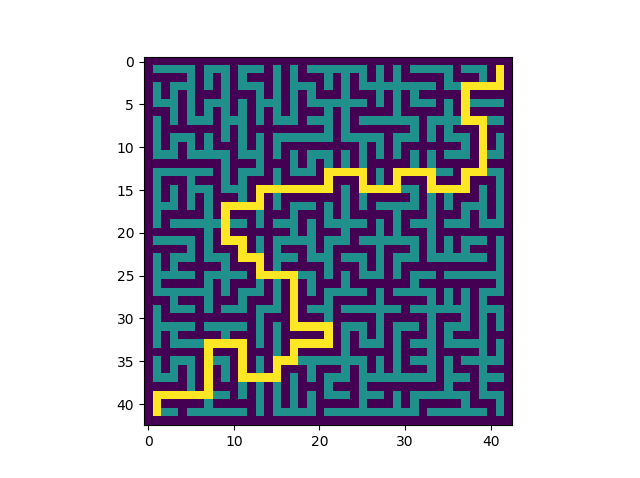
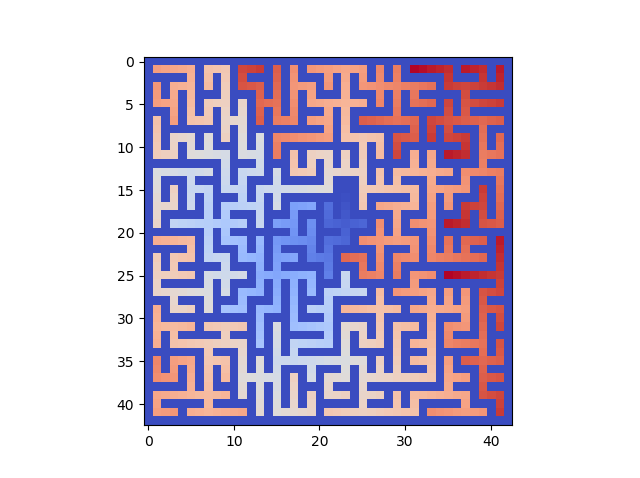
Visualiser les distances...

Pour visualiser les distances, on peut calculer toutes les distances des points du labyrinthe à un point C donné

et modifier les couleurs en fonction de ces distances :

bleu <-> proche, rouge <-> lointain

Distances par rapport au point C, ligne 15, colonne 23

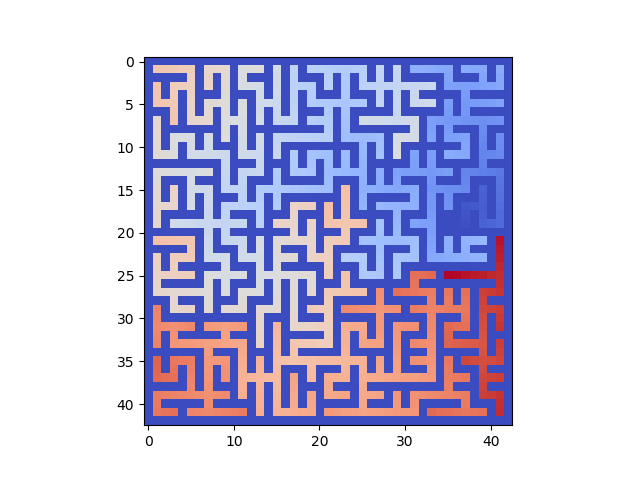
Distances par rapport au point D, ligne 19, colonne 35

Le chemin le plus long partant de D a presque la longueur maximale : 151.

Petit retour en arrière

La configuration initiale est la suivante :

Petit retour en arrière

Si on enlève une colonne sur deux :

Petit retour en arrière

Puis une ligne sur deux :

Petit retour en arrière

Il ne reste plus aucun mur :

Même chose sur un labyrinthe achevé

On part d'un labyrinthe achevé, où on visualise un chemin particulier :

Même chose sur un labyrinthe achevé

On enlève une colonne sur deux :

Même chose sur un labyrinthe achevé

Puis une ligne sur deux :

Même chose sur un labyrinthe achevé

Et on regroupe les cases (forcément vides) restantes :

Quelques exemples

Un labyrinthe ($n=281$, $2n+1=563$)

Quelques exemples

Le plus long chemin dans ce labyrinthe : longueur 4539

Quelques exemples

La carte colorée des distances au point Ligne:475 Colonne:177

HTML("""<video width="960" height="720" controls> <source src="video8.mp4" type="video/mp4"> </video>""")

Quelques exemples

On supprime une ligne sur deux, une colonne sur deux, et on regroupe :

HTML("""<video width="960" height="720" controls> <source src="video7.mp4" type="video/mp4"> </video>""")

HTML("""<video width="960" height="720" controls> <source src="video11.mp4" type="video/mp4"> </video>""")

Bonnes vacances !