(Situation au 8 avril au soir)
Cet article fait suite à mon premier article où je présentais différentes interpolations possibles du nombre de malades testés positifs au CoViD-19.
On peut aussi trouver une explication détaillée des mécanismes du modèle dans un article suivant.
Introduction et mises en garde
L’objectif de cet article est de présenter une analyse rudimentaire de l’évolution du nombre de cas testés positifs au SARS-CoV-2 en France. Il est important de garder à l’esprit que :
- Les données fournies par le gouvernement français concernent le nombre de cas testés positifs : le nombre de malades du CoVid-19 est probablement très supérieur aux données communiquées par le gouvernement.
Les dernières estimations sur ce sujet laissent penser qu’il y a entre 10 et 100 fois plus de malades que de cas testés positifs, ce qui à l’heure où j’écris cet article laisse penser qu’il y a entre 50 000 et 500 000 malades en France, voire davantage encore.
Les raisons pour lesquelles le nombre de cas testés positifs est si sous-évalué par rapport au nombre de malades sont diverses, mais on peut par exemple citer l’existence de très nombreux cas de malades asymptomatiques, c’est-à-dire ne présentant pas ou peu de symptômes : voir ici par exemple. - Je tente d’interpoler les données du nombre de cas testés positifs à l’aide d’une sigmoïde. À ce titre, il convient de bien comprendre que :
- mon modèle est purement mathématique et ne reflète en aucun cas la complexité des processus biologiques en jeu;
- mon modèle a une portée essentiellement pédagogique visant à faire comprendre que l’interpolation exponentielle ne peut pas être valide sur le long terme : le nombre de cas testés positifs tendra vers une valeur finie dans un pays à population finie;
- l’objectif de cet article est de tester la robustesse du modèle. On verra que la dernière version en date semble relativement robuste et permet de fournir une prévision relativement fiable du nombre de cas testés positifs à un jour près. Cependant, parce qu’il s’agit d’une simple interpolation, il ne peut prendre en compte l’évolution de la politique sanitaire et pourrait par exemple sur-évaluer le nombre futur de cas puisque la fermeture des établissements scolaires et universités annoncée le 12 mars, ou encore celle des débits de boisson et autres boîtes de nuit annoncée le 14 mars auront, très probablement, pour conséquence d’enrayer la diffusion du virus. De ce point de vue, le modèle pourrait permettre d’observer l’efficacité de ces mesures : plus il sur-évaluera les annonces du nombre de nouveaux cas, plus les mesures de confinement se seront montrées efficaces.
- Je fais amende honorable pour les premières versions de mon algorithme qui sous-évaluaient grandement la vitesse de contagion. L’objectif de cet article est aussi de corriger mes premières erreurs.
- Pour une analyse bien plus détaillée de l’épidémie et notamment de la nécessité d’un confinement aussi strict que possible, on peut consulter cet excellent article en anglais.
Principe de l’algorithme
Je pars du postulat qu’une approximation grossière du nombre de cas testés positifs peut être obtenue à l’aide d’une sigmoïde :
\[N(t)=\dfrac{c}{1+e^{-a(t-t_0)}}\]où :
- $c$ représente le nombre asymptotique de cas testés positifs en fin d’épidémie;
- $a$ représente la contagiosité du virus en début d’épidémie - plus précisément $\alpha=e^a-1$ représente la proportion de nouveaux cas par jour en tout début d’épidémie;
- $t_0$ représente le moment où l’inflexion se produit, c’est-à-dire le moment où le nombre de nouveaux cas par jour commence à diminuer - de façon pérenne - par rapport aux nombres observés dans le passé.
La difficulté est d’obtenir les constantes réelles $a$, $c$ et $t_0$ sur la base des données fournies par les autorités sanitaires tous les soirs depuis plusieurs semaines.
La méthode que j’utilise est la suivante :
- pour beaucoup de valeurs de $c$ comprises entre le nombre de cas testés positifs actuels et le nombre d’habitants en France, on obtient $a$ et $t_0$ à l’aide d’une régression linéaire (je préciserai plus loin comment j’effectue cette régression);
- on retient la valeur de $c$ minimisant la somme des carrés des écarts entre les données fournies et les prévisions faites par le modèle;
- on retient aussi une valeur $c_M$ supérieure à $c$ pour laquelle la somme des carrés entre données et prévisions est inférieure à $1,5$ fois la valeur optimale précédemment calculée. Cette valeur $c_M$, ainsi que les valeurs $a_M$ et $t_M$ correspondantes, seront appelées par la suite coefficients de l’hypothèse pessimiste.
Concernant la régression linéaire permettant d’obtenir $a$ et $t_0$ :
- de façon équivalente au postulat émis sur le nombre de cas, on a $a(t-t_0)\approx \ln\left(\frac{N(t)}{c-N(t)}\right)$.
Partant des données officielles, on calcule donc $L(t)=\ln\left(\frac{N(t)}{c-N(t)}\right)$ pour chaque valeur de $c$ retenue et pour les valeurs de $N$ connues. - Ces valeurs de $L(t)$ sont alors pondérées par la valeur de $N(t)$ : c’est la principale différence avec l’algorithme que je présentais dans mon précédent article.
L’objectif est double :- Faire en sorte que l’optimisation des coefficients $a$ et $t_0$ minimise un écart tenant compte de l’importance croissante du nombre de cas testés positifs;
- Attribuer un poids plus important aux dernières données obtenues pour tenir compte des évolutions récentes de l’épidémie.
Codes Python
On note $b=-at_0$ de sorte à ce que $N(t)=\dfrac{c}{1+e^{-(at+b)}}$ et $at+b\approx \ln\left(\frac{N(t)}{c-N(t)}\right)$.
Le code Python pour la régression linéaire, la fonction sigmoïde et l’interpolation numérique :
def reglin(X,Y,poids=None):
"""Calcul des coefficients de la droite de régression Y = a*X+b où chaque
point (x_i,y_i) est pondéré par le poids donné dans la liste optionnelle."""
if poids is None:
poids=np.ones((len(X),))
poids = np.array(poids)
N = np.sum(poids)
moyX = sum(poids*X)/N
moyY = sum(poids*Y)/N
a = sum(poids*(X-moyX)*(Y-moyY)/N)/sum(poids*(X-moyX)**2/N)
b = moyY-a*moyX
return a,b
def f(a,b,c):
"""Renvoie la fonction sigmoïde correspondante."""
return lambda x:c/(1+np.exp(-(a*x+b)))
def interpSigm(data,deb,fin,S0=0,mxS=1e6,err=1.5,nbInt=500):
"""Calcule les paramètres (a,b,c) de la sigmoïde ainsi que les versions
optimiste : (am,bm,cm)
pessimiste : (aM,bM,cM)"""
n = len(data)
somcum = [S0+sum(data[:(k+1)]) for k in range(n)]
mn=np.infty
X = np.array(range(deb,fin))
tab = []
for c in np.exp(np.linspace(np.log(1+max(somcum[deb:fin])),np.log(mxS),nbInt)):
Y0 = np.log(somcum/(c-somcum))[deb:fin]
a,b = reglin(X,Y0,somcum[deb:fin])
fX = f(a,b,c)(X)
S = sum((somcum[deb:fin]-fX)**2)
tab.append((a,b,c,S))
if S<=mn:
am,bm,cm = a,b,c
mn = S
a,b,c = am,bm,cm
tab = [k for k in tab if k[3]<err*mn]
am,bm,cm = tab[0][:3]
aM,bM,cM = tab[-1][:3]
return ((am,bm,cm),(a,b,c),(aM,bM,cM))
L’obtention de quelques paramètres supplémentaires à partir de ceux interpolés :
def caracteristiques(a,b,c,d):
"""Calcule trois paramètres caractéristiques
- taux de croissance instantané
- taux de croissance en -infini
- jour d'inflexion
à partir des valeurs de (a,b,c)
et de celle du jour d pour lequel on cherche la croissance instantanée."""
taux = a*np.exp(-(a*d+b))/(1+np.exp(-(a*d+b)))
tauxInit = np.exp(a)-1
inflexion = -b/a
return taux,tauxInit,inflexion
Évaluation de la robustesse du nouvel algorithme
Pour commencer, quelle que soit la méthode utilisée, un algorithme visant à interpoler des données par une sigmoïde postulée comme étant valide sur le long terme, est à priori très sensible aux fluctuations et erreurs de mesure des données dans un premier temps :
- la première raison est que la pente de la sigmoïde tend vers 0 lorsque $t\to-\infty$. Une erreur de mesure se répercute donc très fortement sur l’évaluation des paramètres de la sigmoïde.
- une autre raison est que les valeurs à interpoler sont très faibles pour $t\to-\infty$ et que - par conséquent - on ne peut pas encore considérer qu’une moyenne statistique lisse les erreurs de mesures.
Dans un premier temps, donc, les valeurs obtenues pour les paramètres statistiques sont - au mieux - très approximatives, ou - au pire - totalement aberrantes.
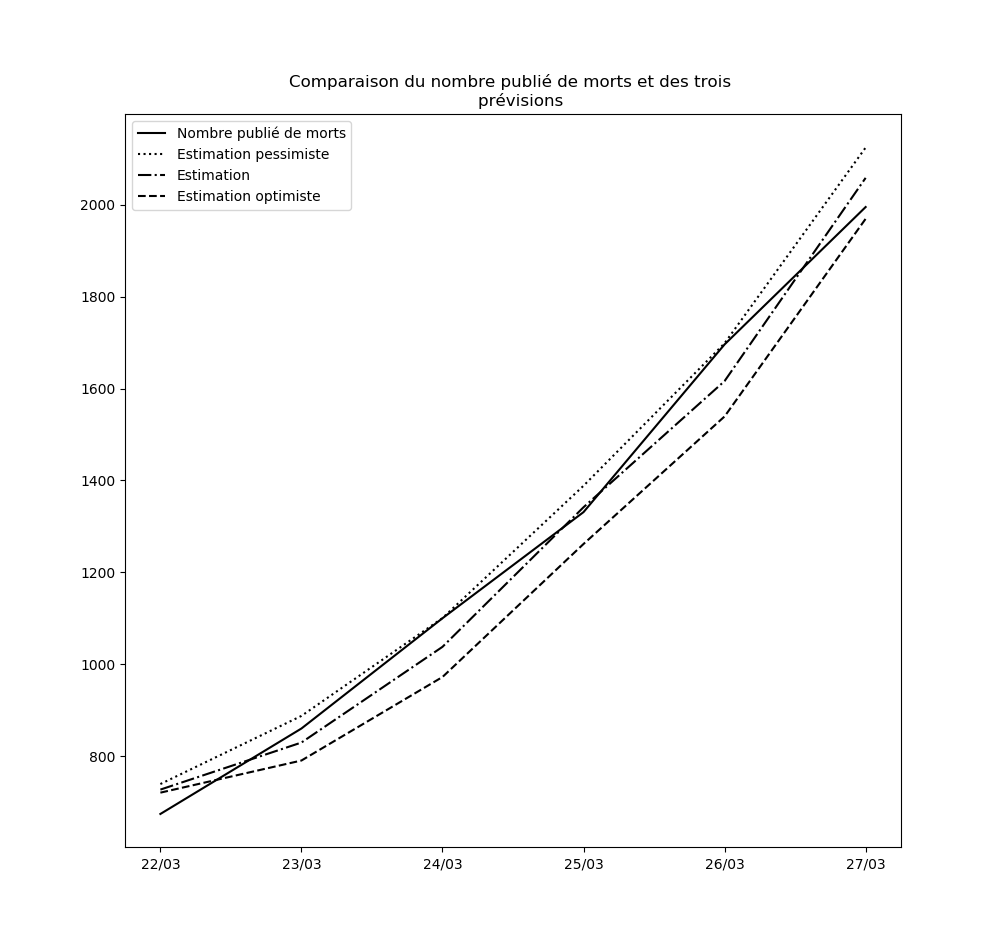
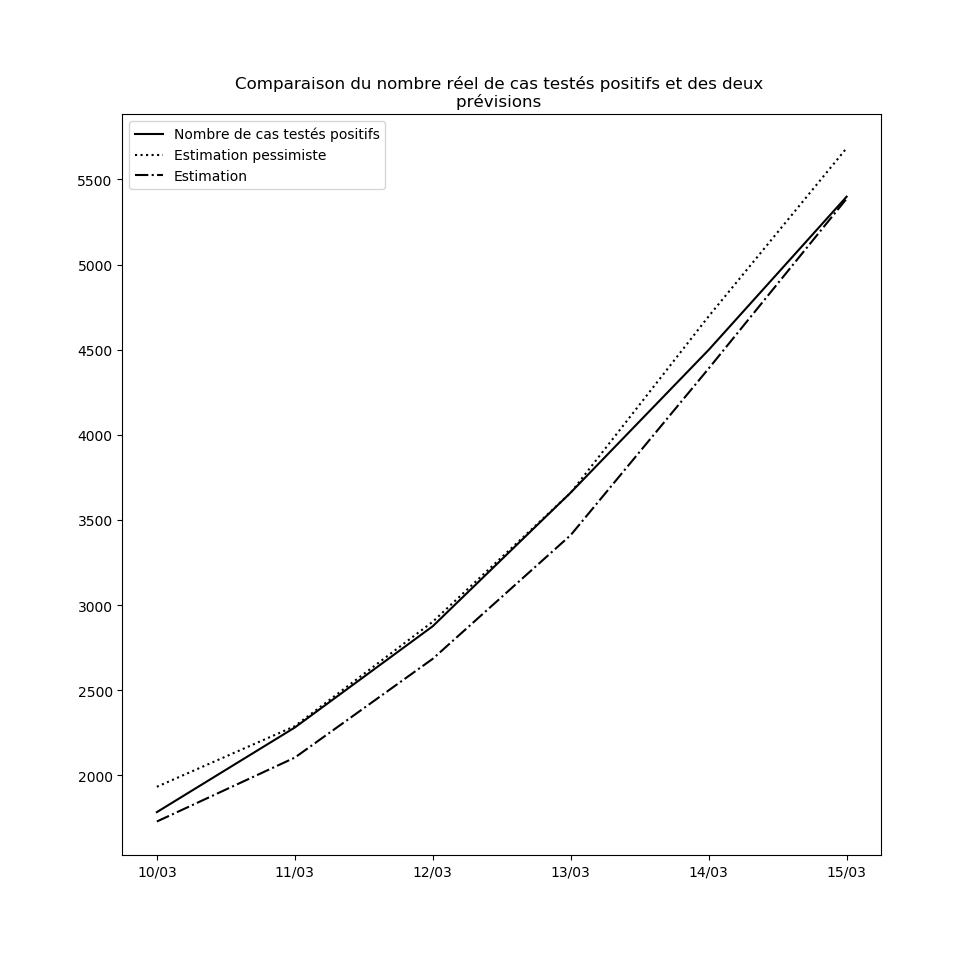
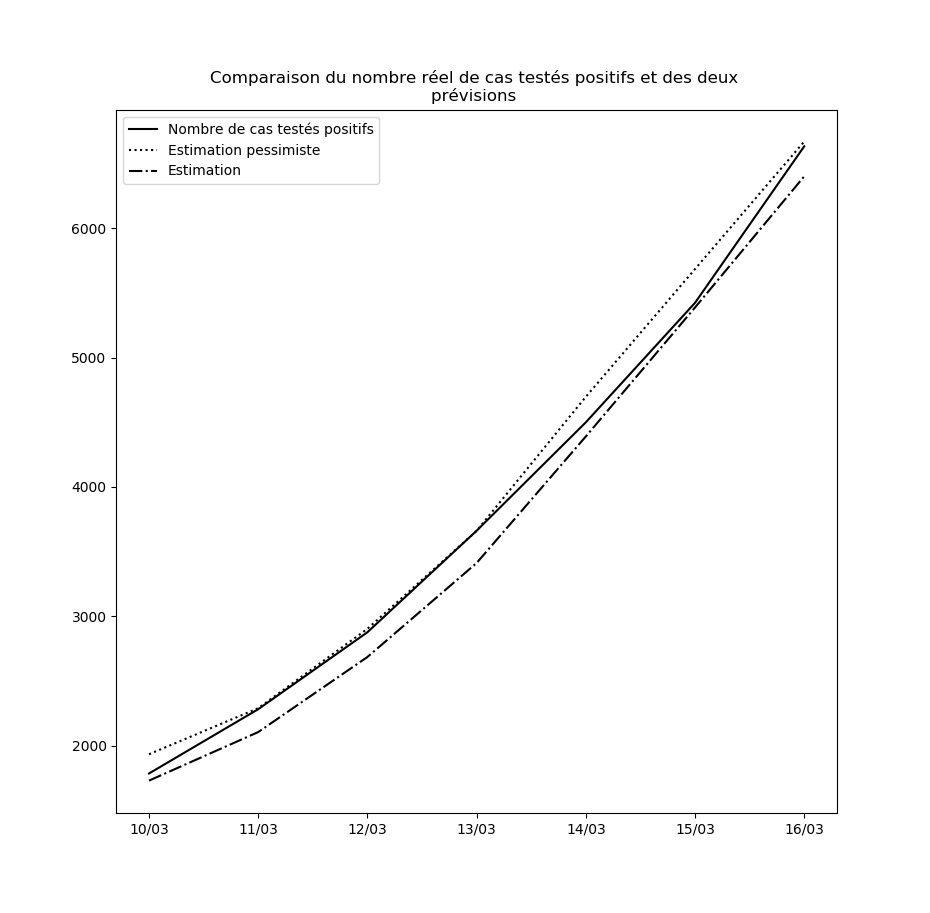
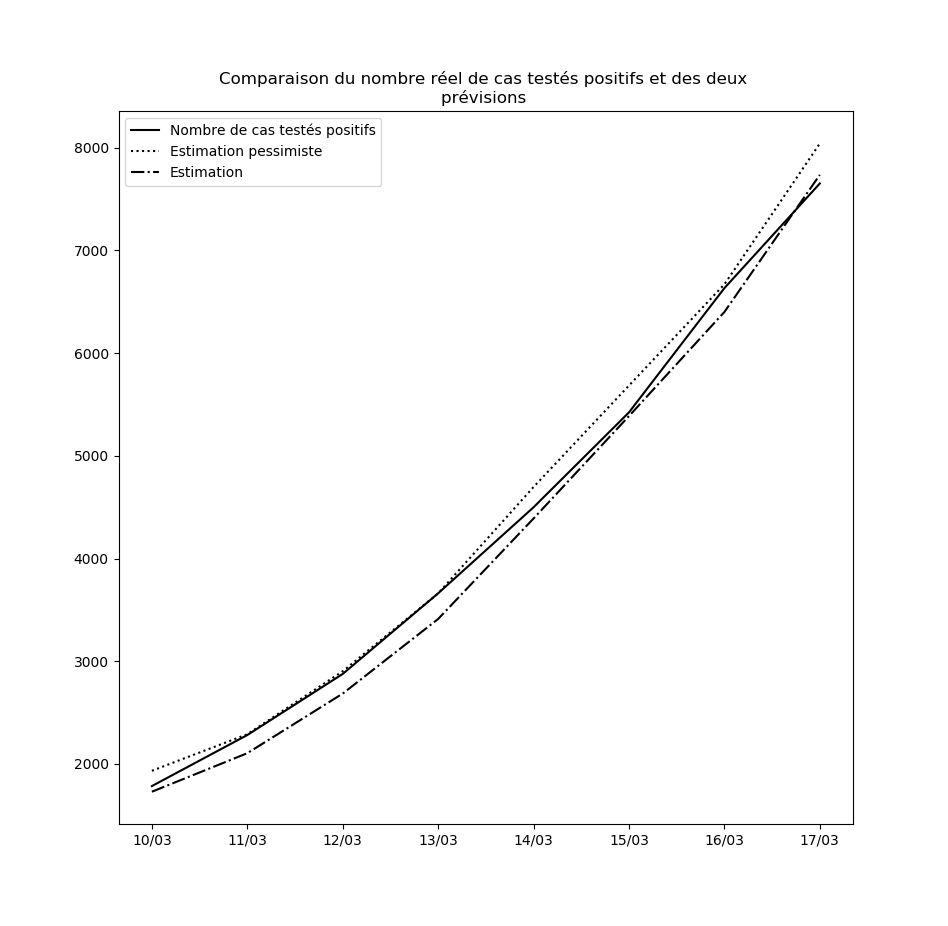
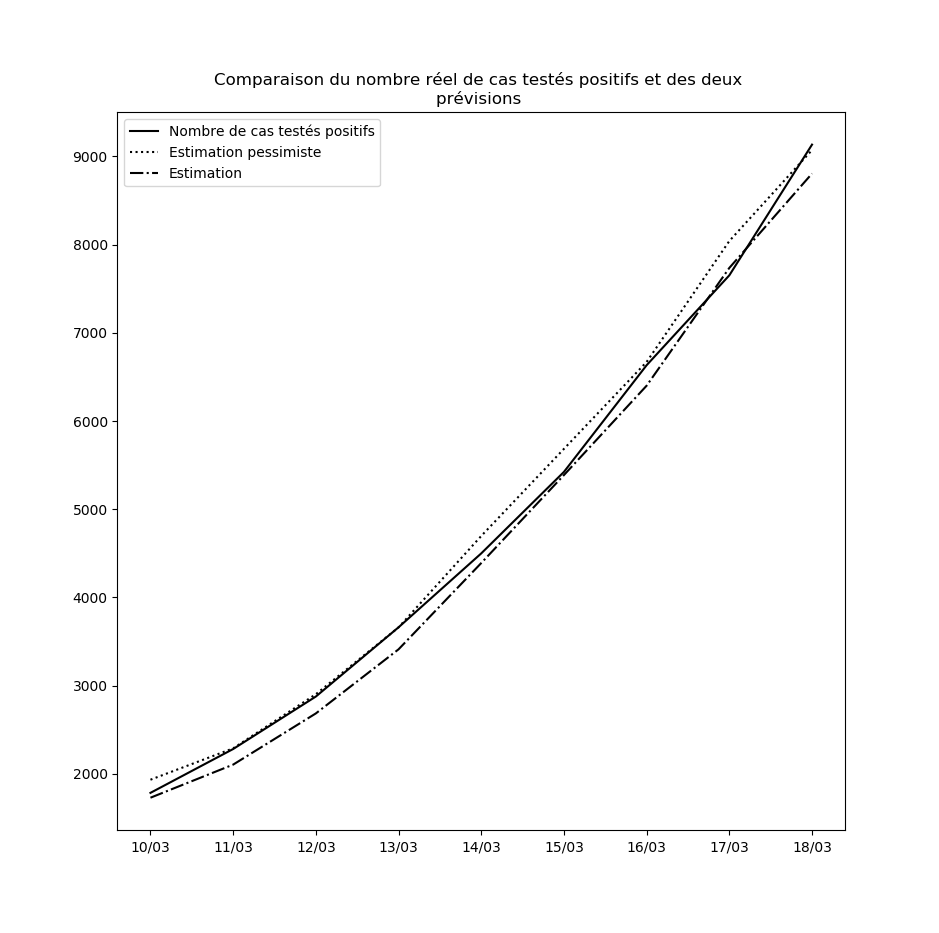
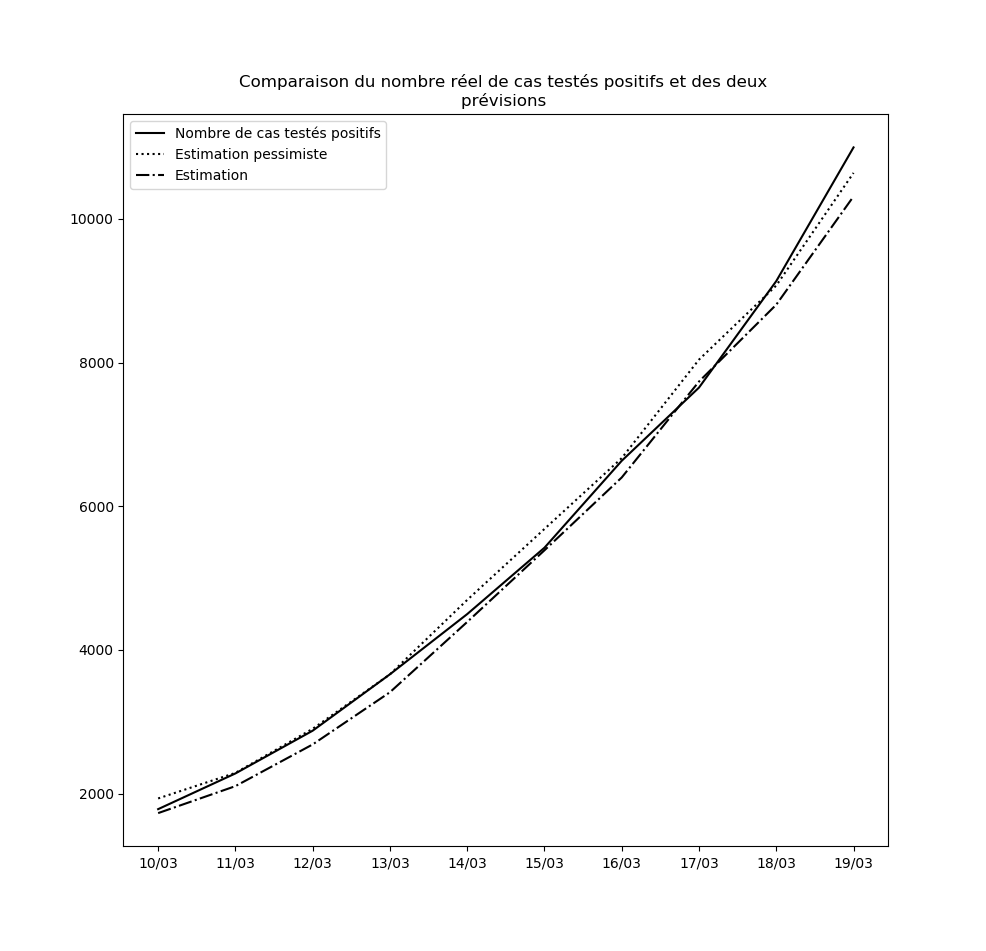
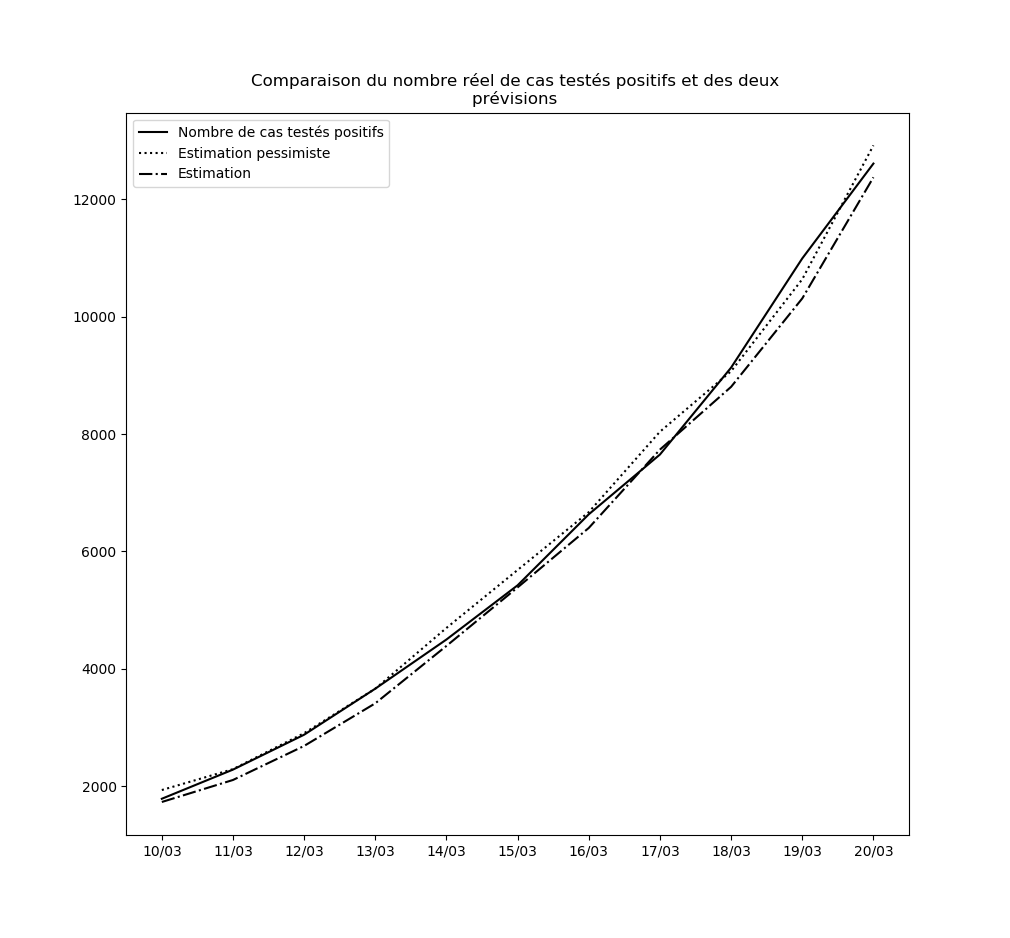
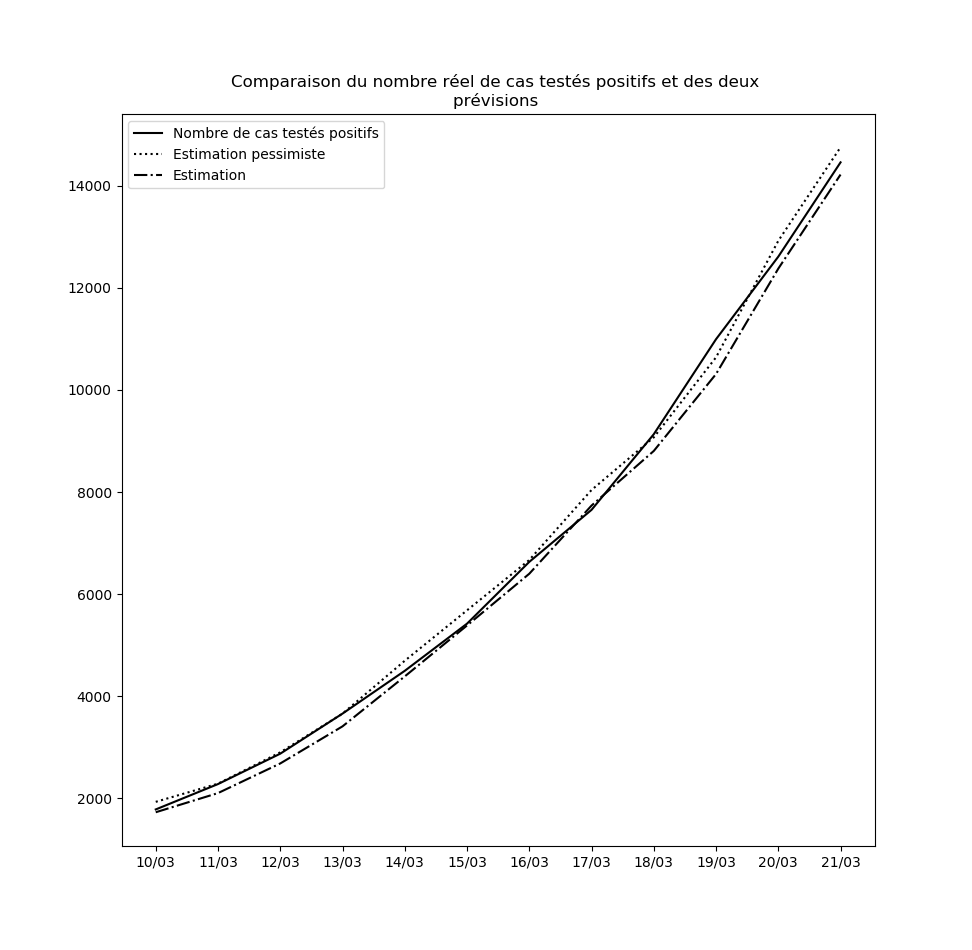
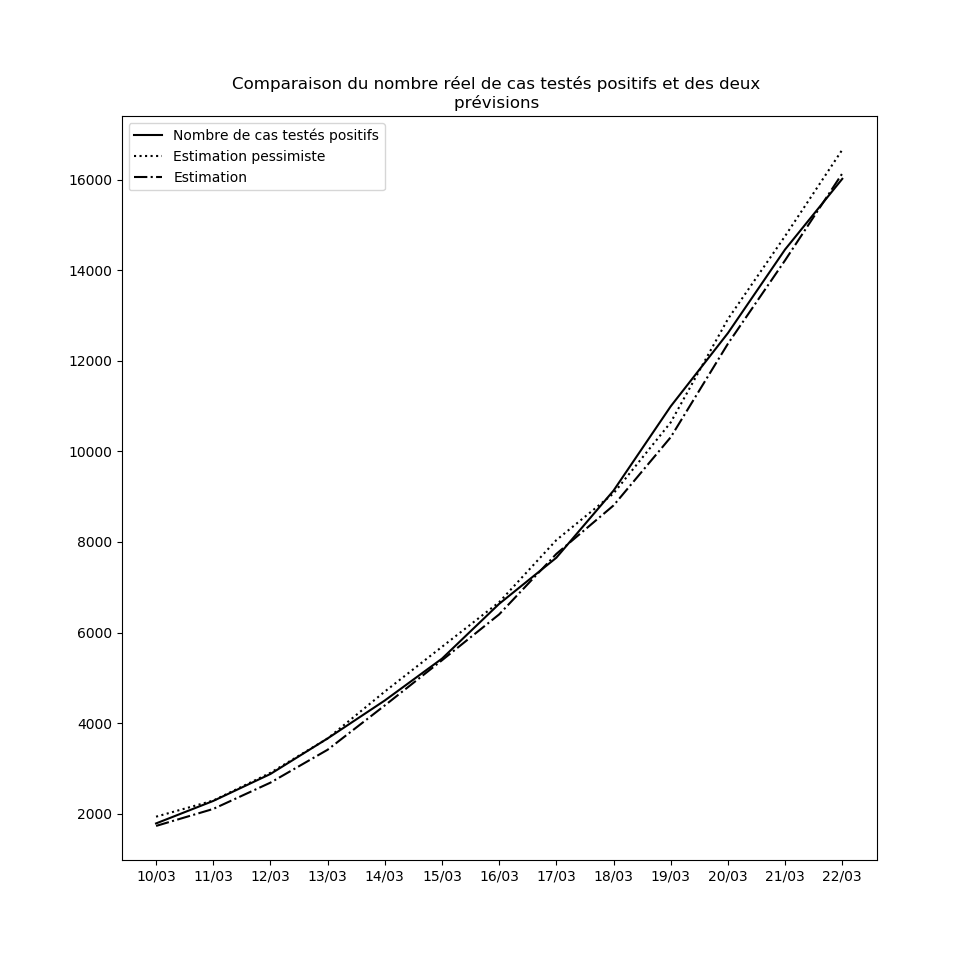
Concernant le nouvel algorithme que j’ai présenté plus haut, voici la comparaison entre les nombres de cas prédits à un jour par l’interpolation et l’interpolation pessimiste d’une part, et le nombre réel de cas testés positifs d’autre part, depuis le 10 mars jusqu’au 14 mars :
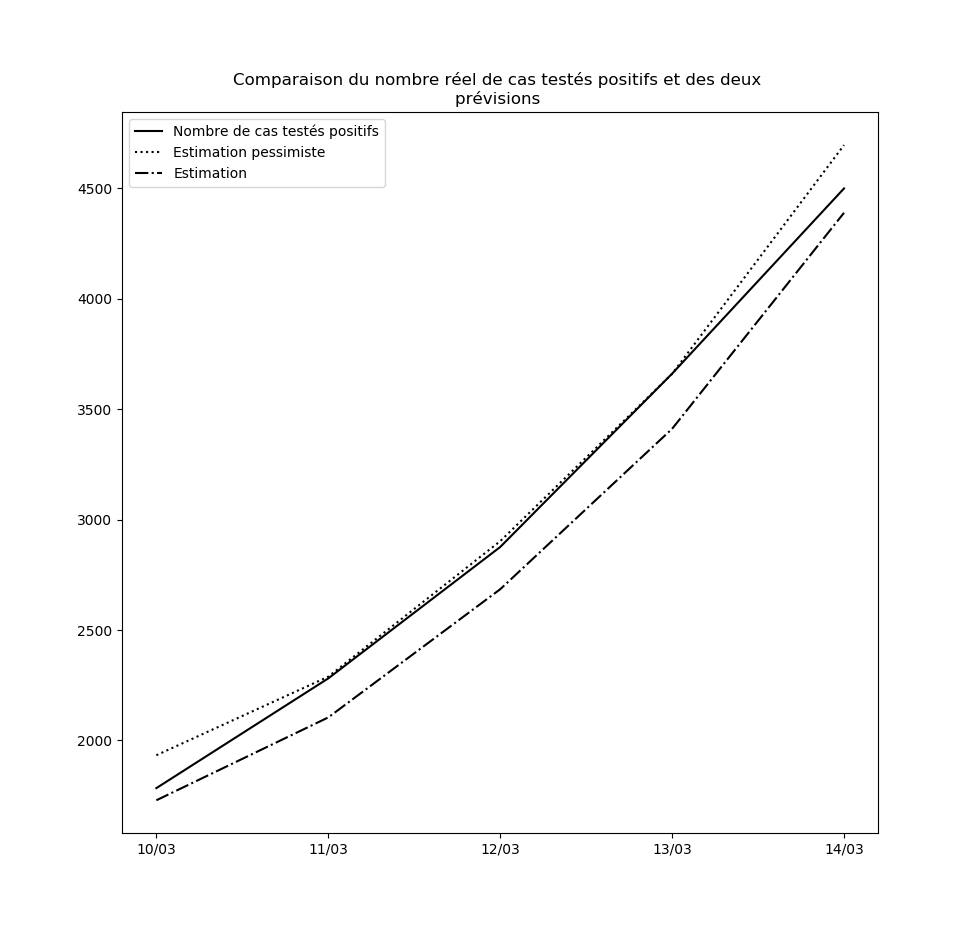
Je n’ai pas choisi le 10 mars par hasard : le 9 mars, une brusque augmentation du nombre de nouveaux cas a eu pour conséquence que l’hypothèse pessimiste a prédit - ponctuellement - un nombre asymptotique de cas testés positifs égal à la population française.
Ceci pourrait éventuellement se reproduire : il ne faut pas accorder une confiance démesurée aux prédictions de l’interpolation obtenue. Mais elle permet tout de même d’observer que pour l’instant, rien n’enraye la propagation du virus à l’échelle nationale. Dans la mesure où le temps d’incubation médian est de l’ordre de 5 jours (voir ici par exemple), les mesures prises depuis vendredi auront un effet en fin de semaine prochaine. Je mettrai à la fin de cet article des mises-à-jour régulières des graphiques où ces effets devraient pouvoir être visibles : une diminution de la propagation du virus devrait se traduire par une inversion de la courbe donnant le nombre de cas testés positifs et de celle donnant la prédiction par la meilleure interpolation.
Stabilité des constantes de l’interpolation
Pour l’instant, aucune des constantes d’interpolation ne converge. Le modèle ne peut donc être considéré ni comme stable, ni comme valide sur le long terme.
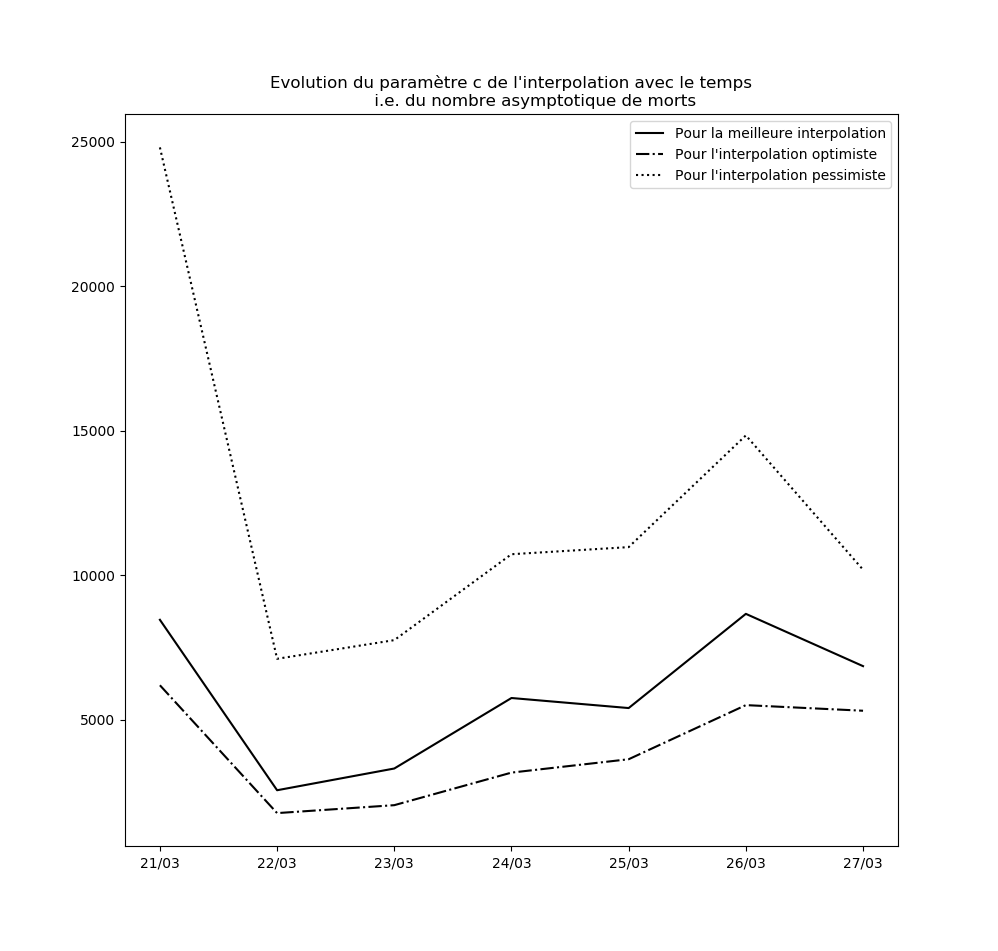
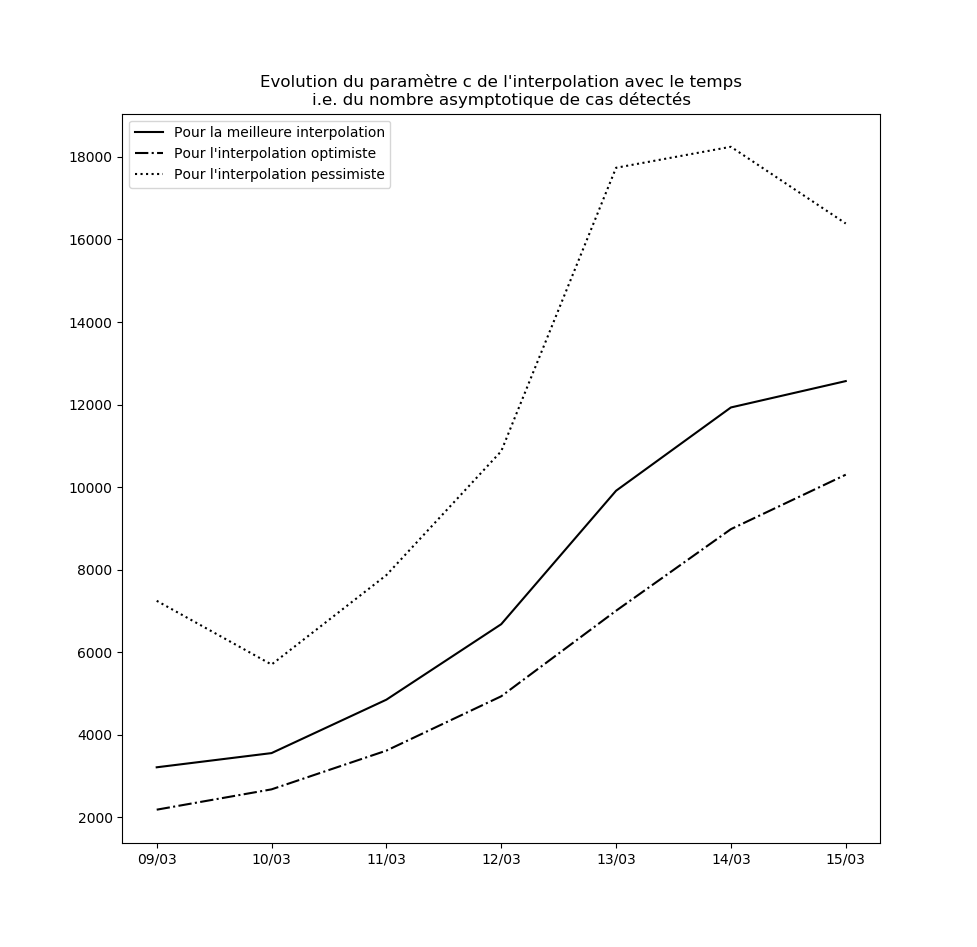
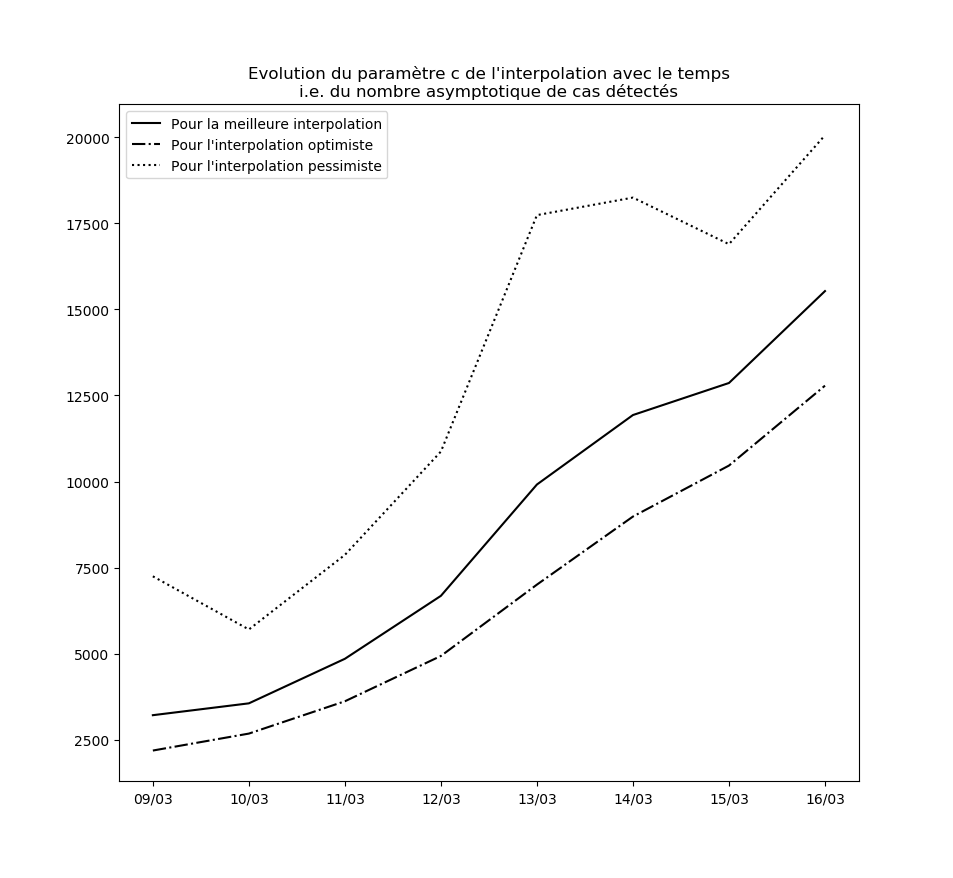
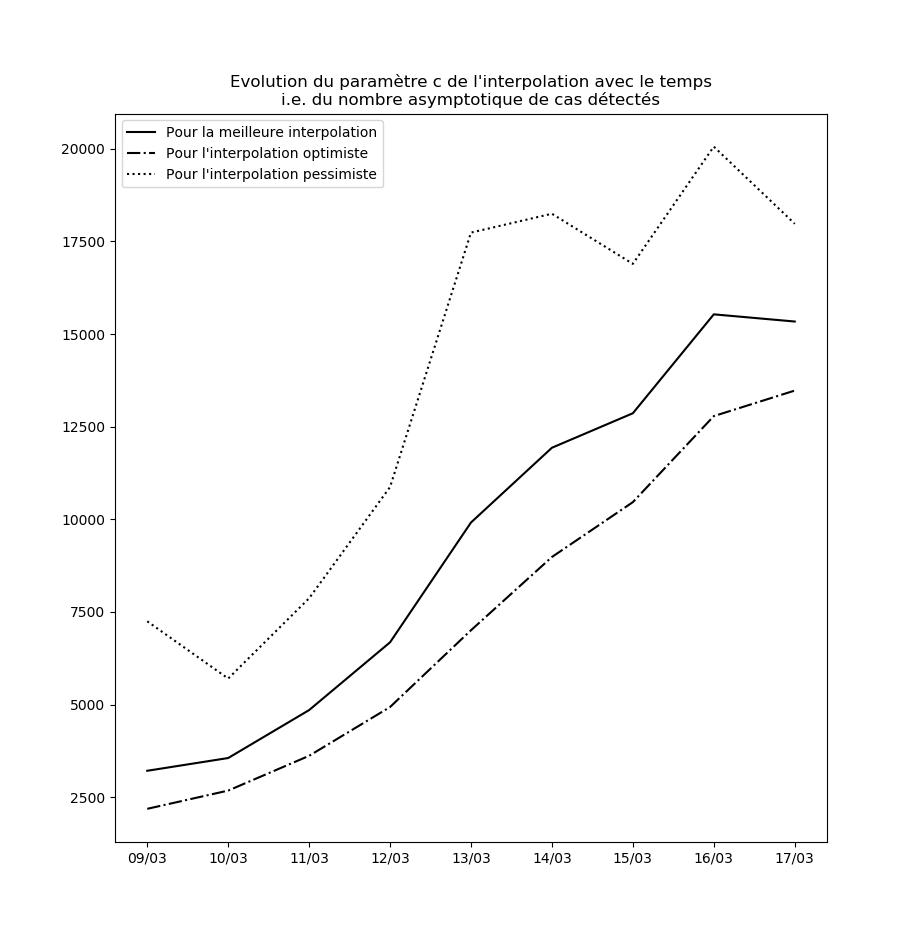
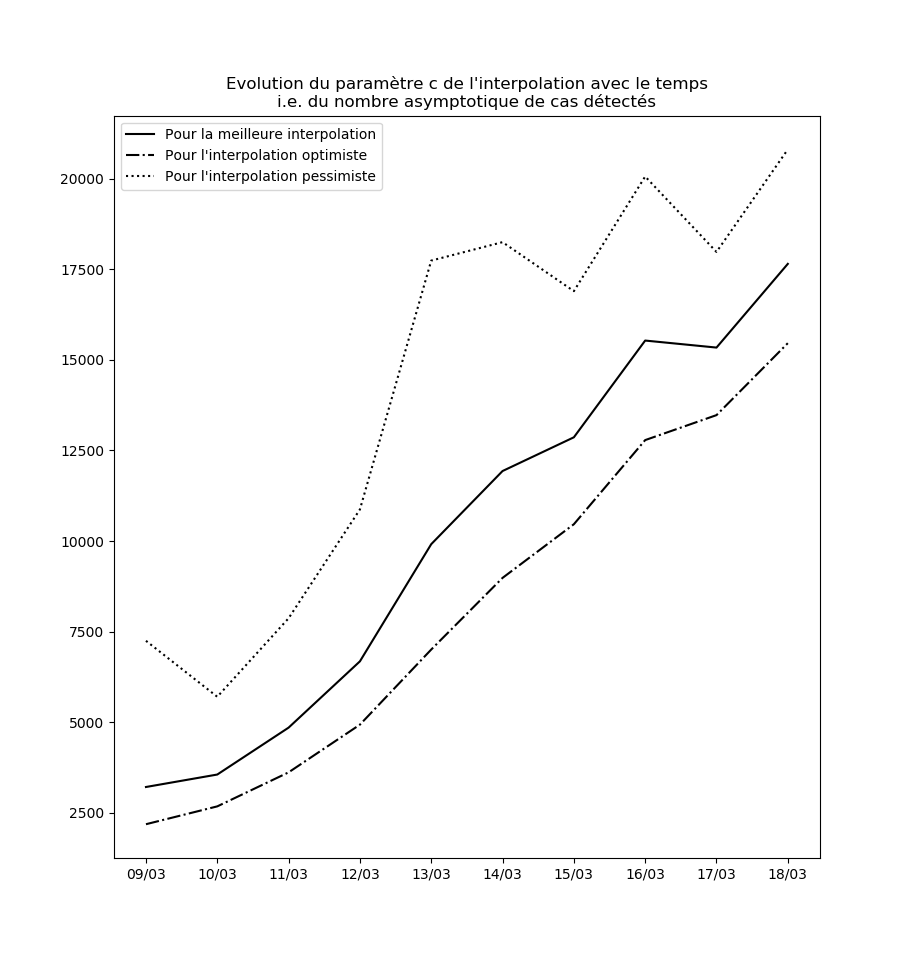
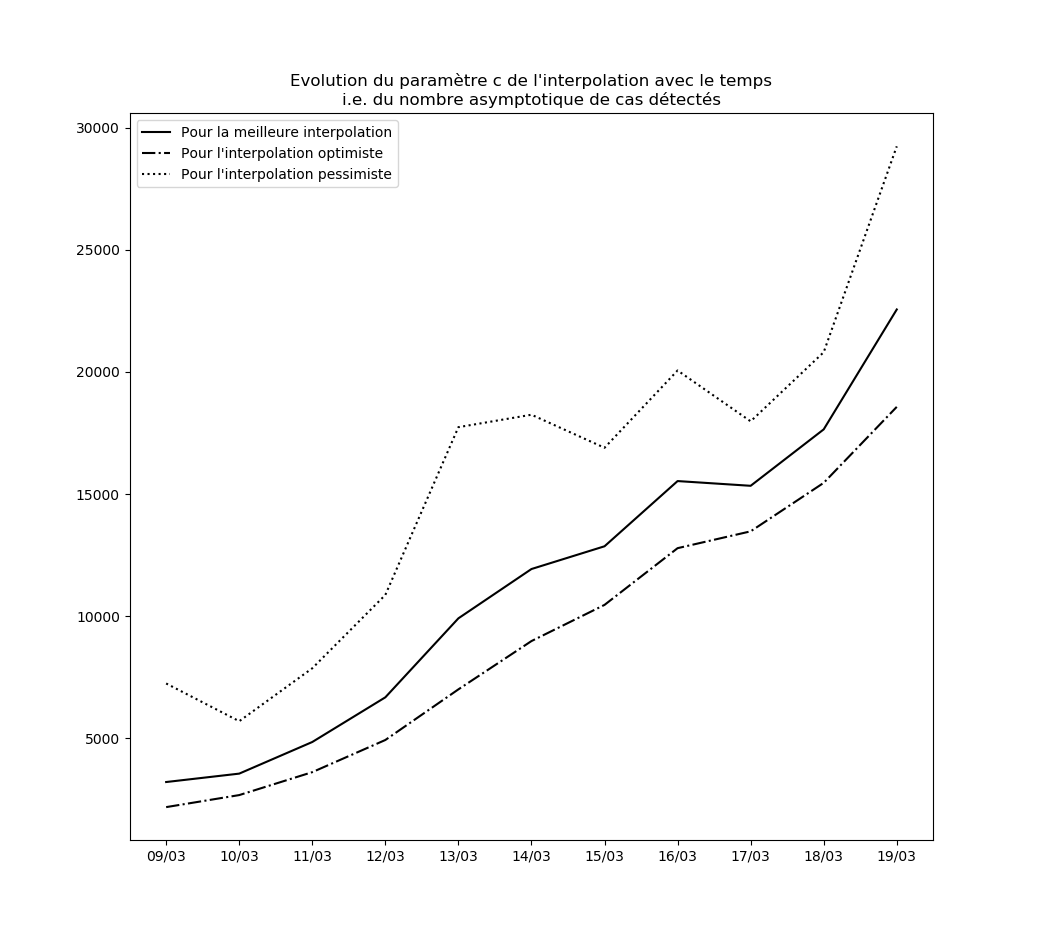
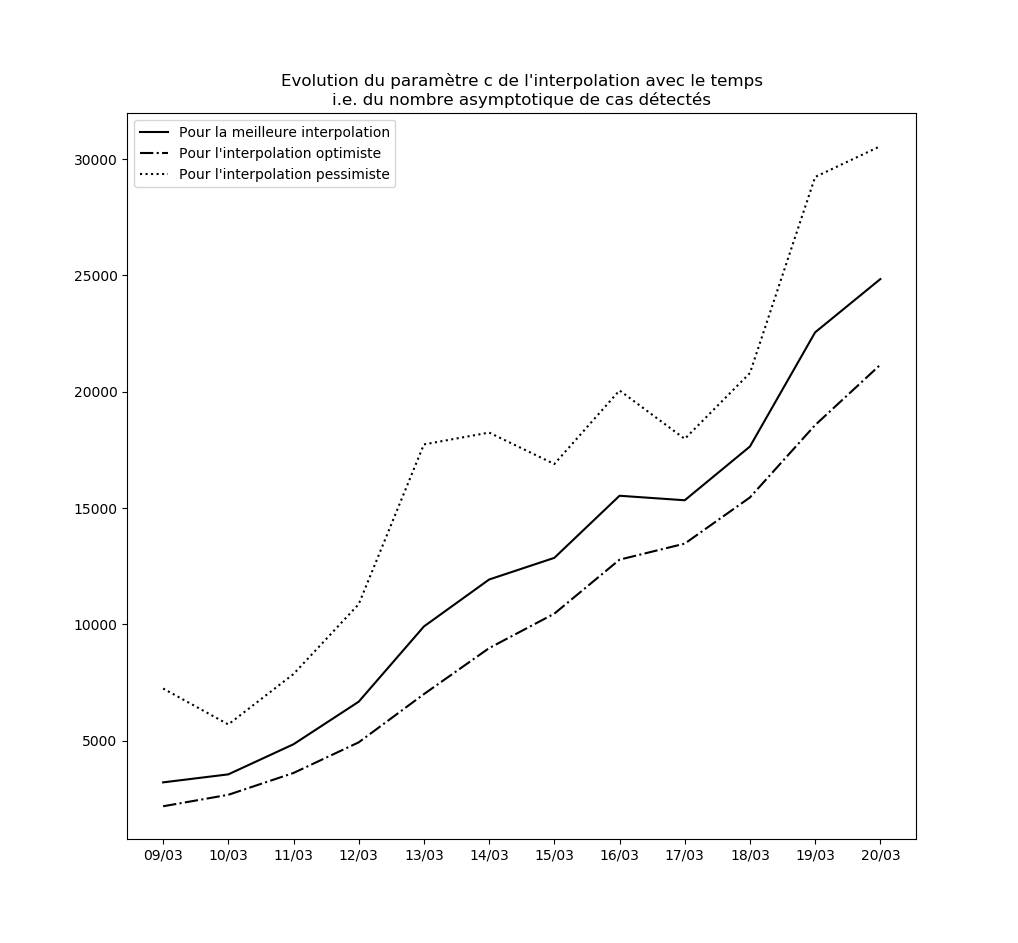
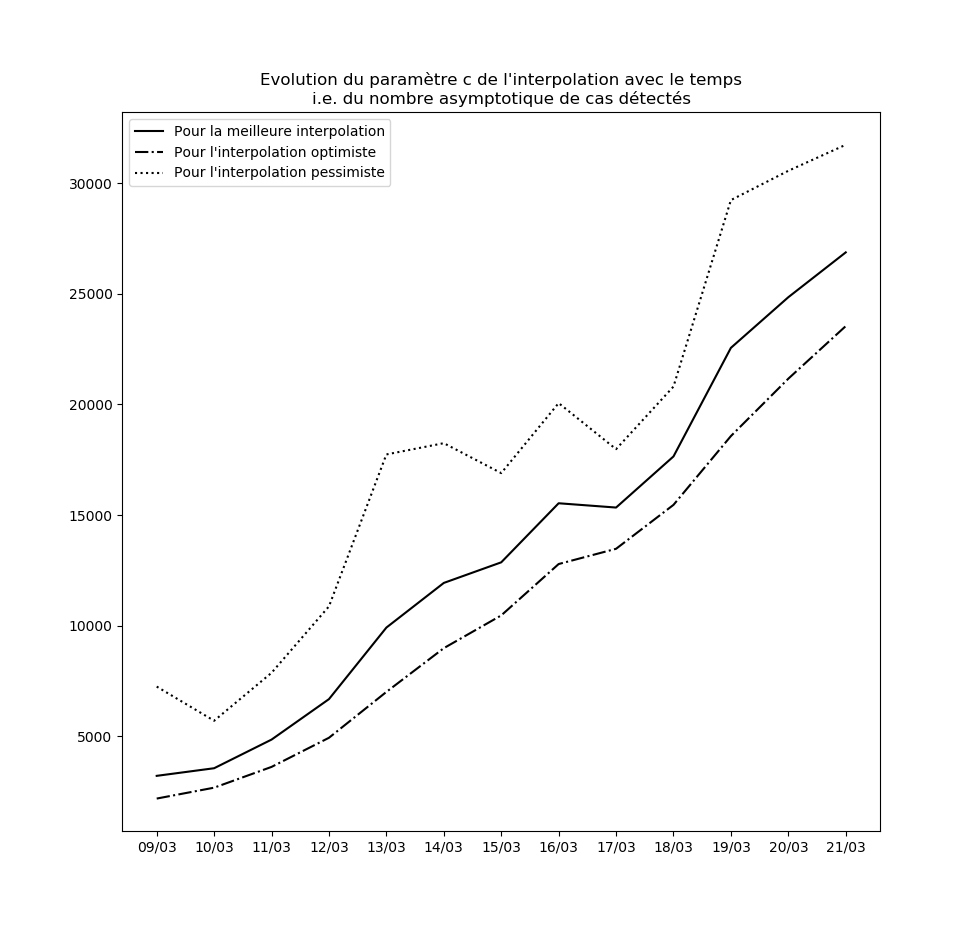
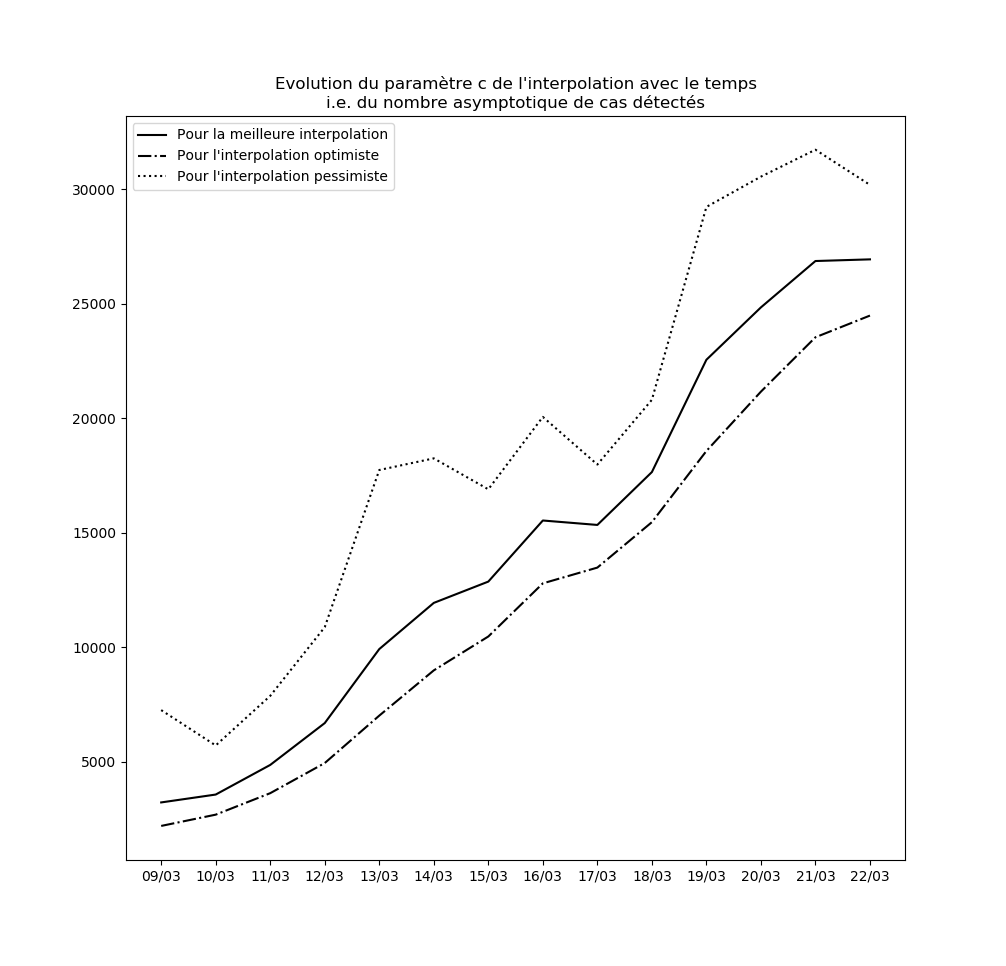
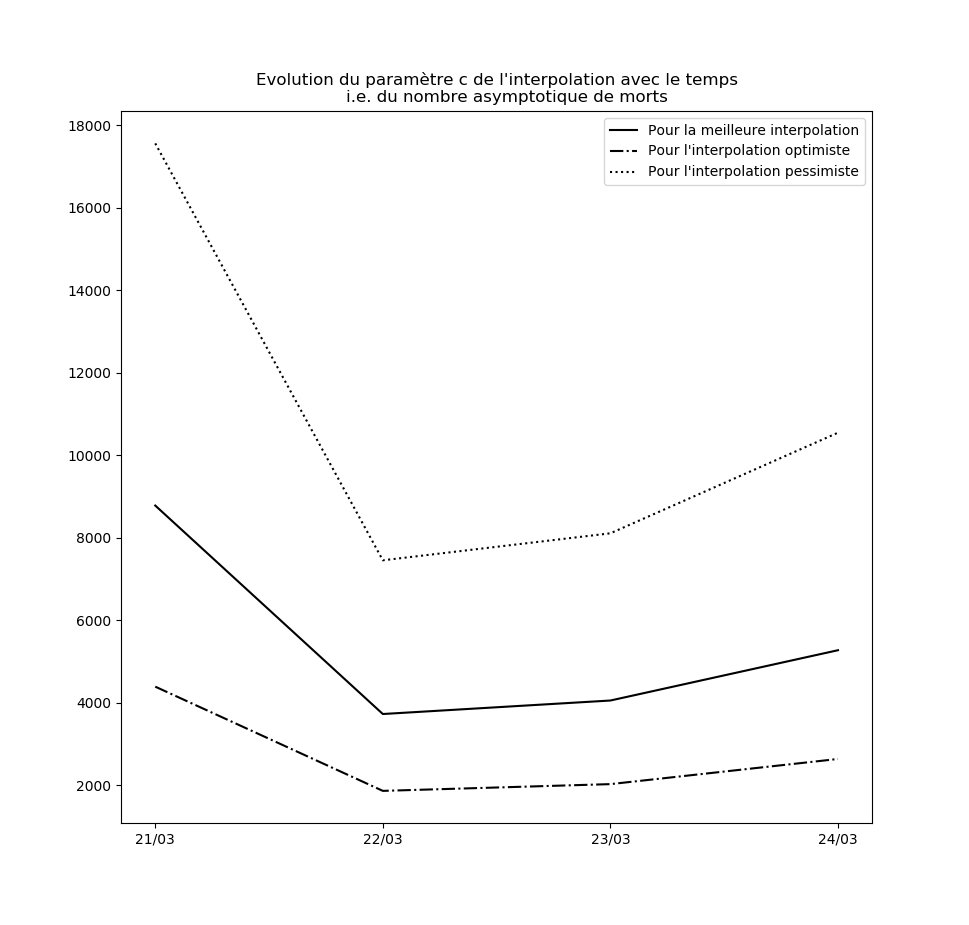
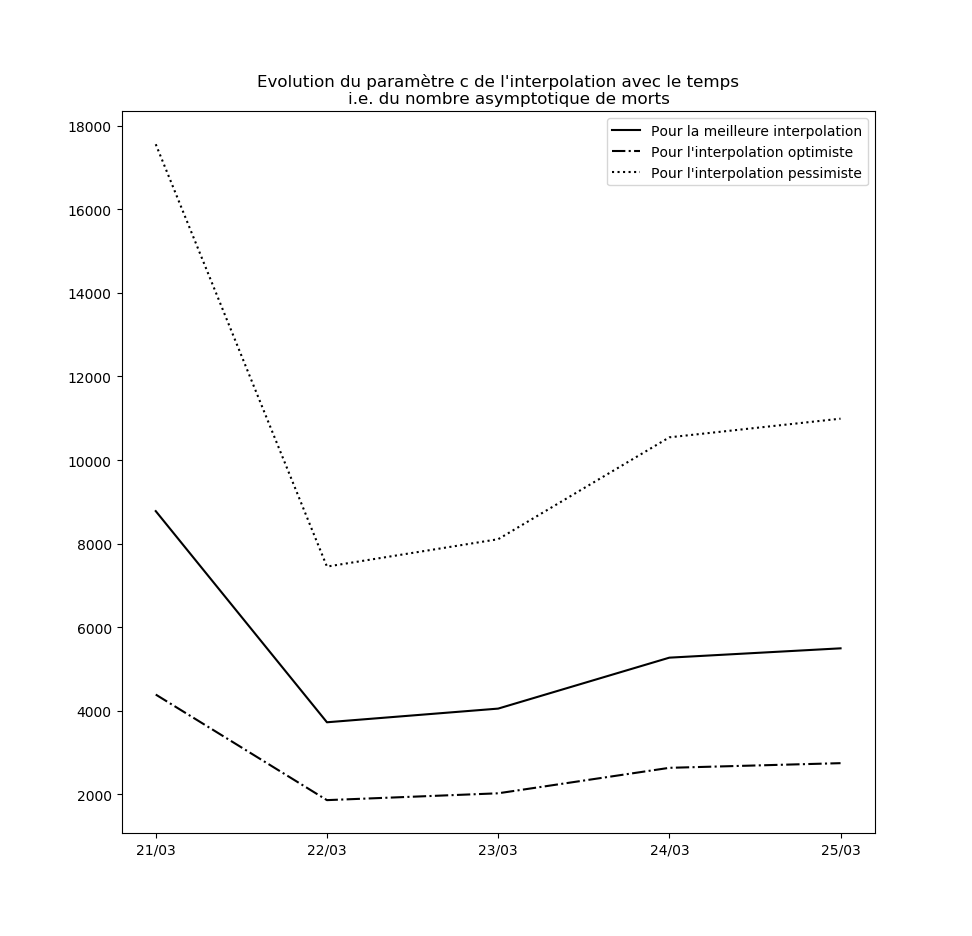
L’évolution des constantes d’interpolation avec le temps montre en fait une dégradation de la situation - qui semble justifier les mesures drastiques prises par le gouvernement hier (à savoir les annonces du Premier ministre le 14 mars). Voici par exemple l’évolution du paramètre $c$ : il s’agit des prédictions faites par le modèle concernant le nombre maximal de cas testés positifs en fin d’épidémie sur la base des données connues jusqu’au 9 mars, jusqu’au 10 mars, etc…
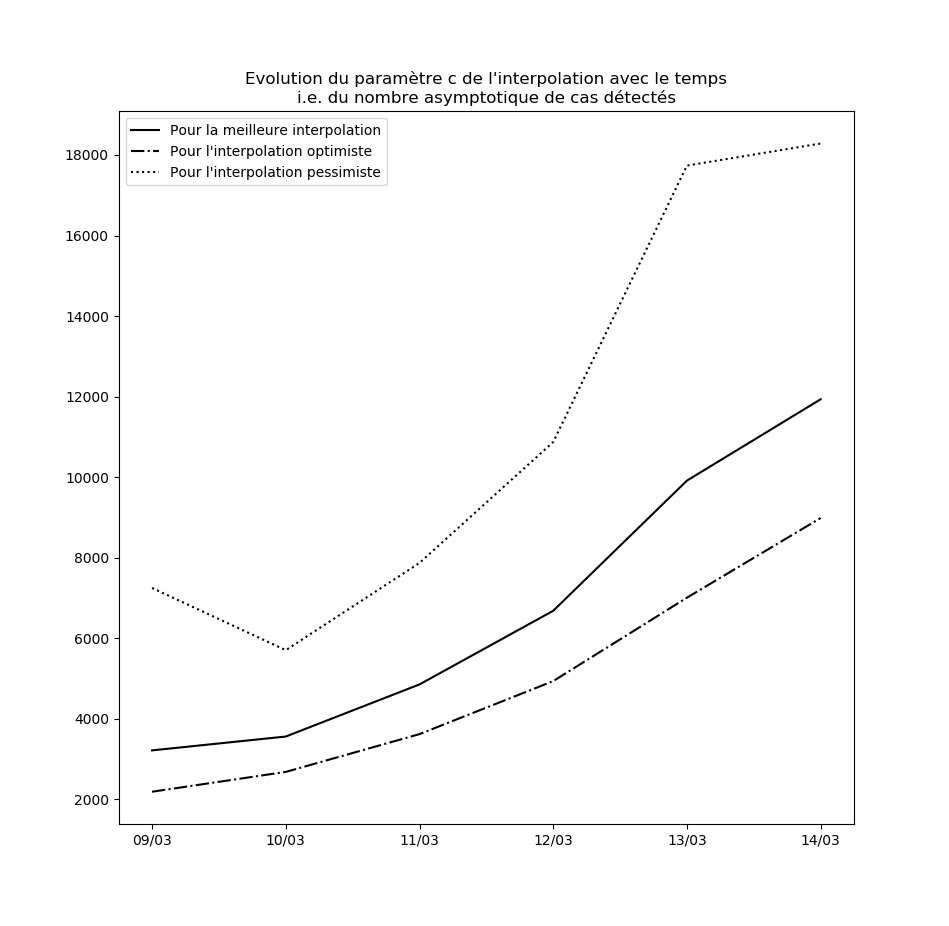
Une amélioration de la situation se traduirait par une stabilisation, voire par une baisse, de cette valeur.
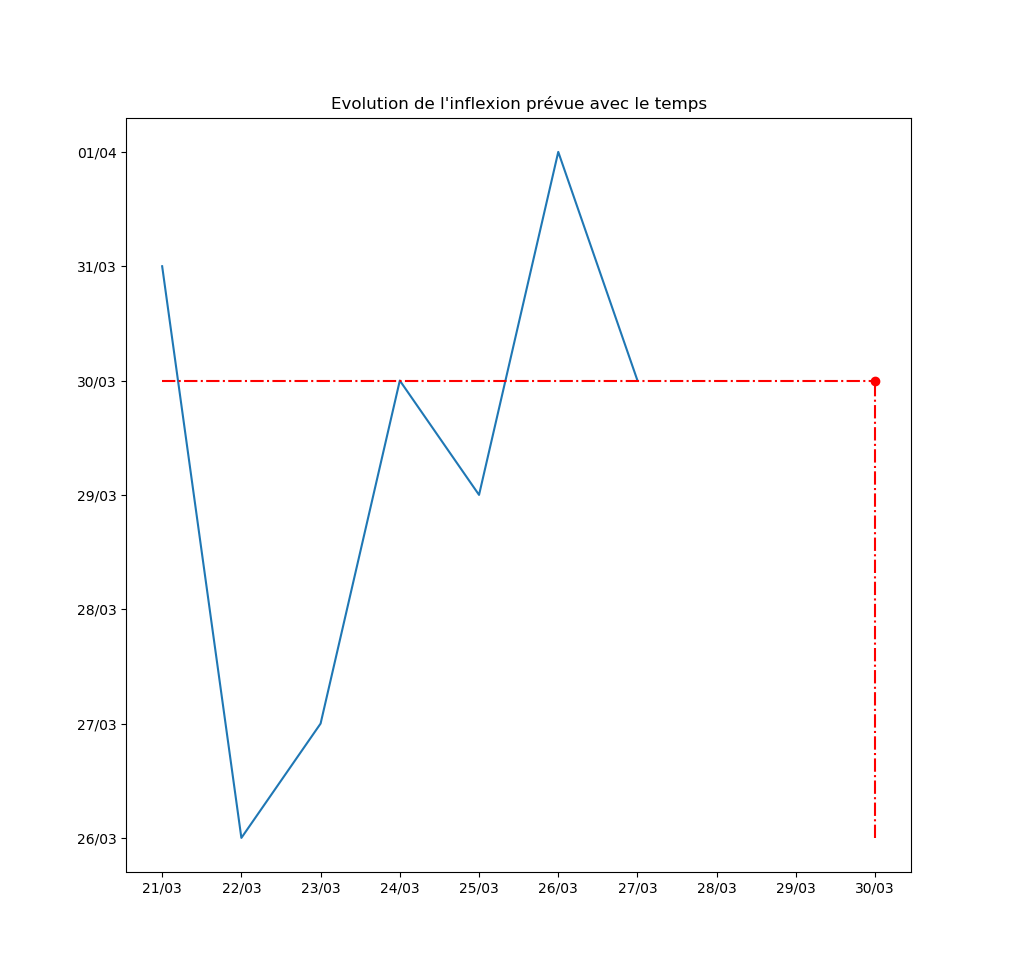
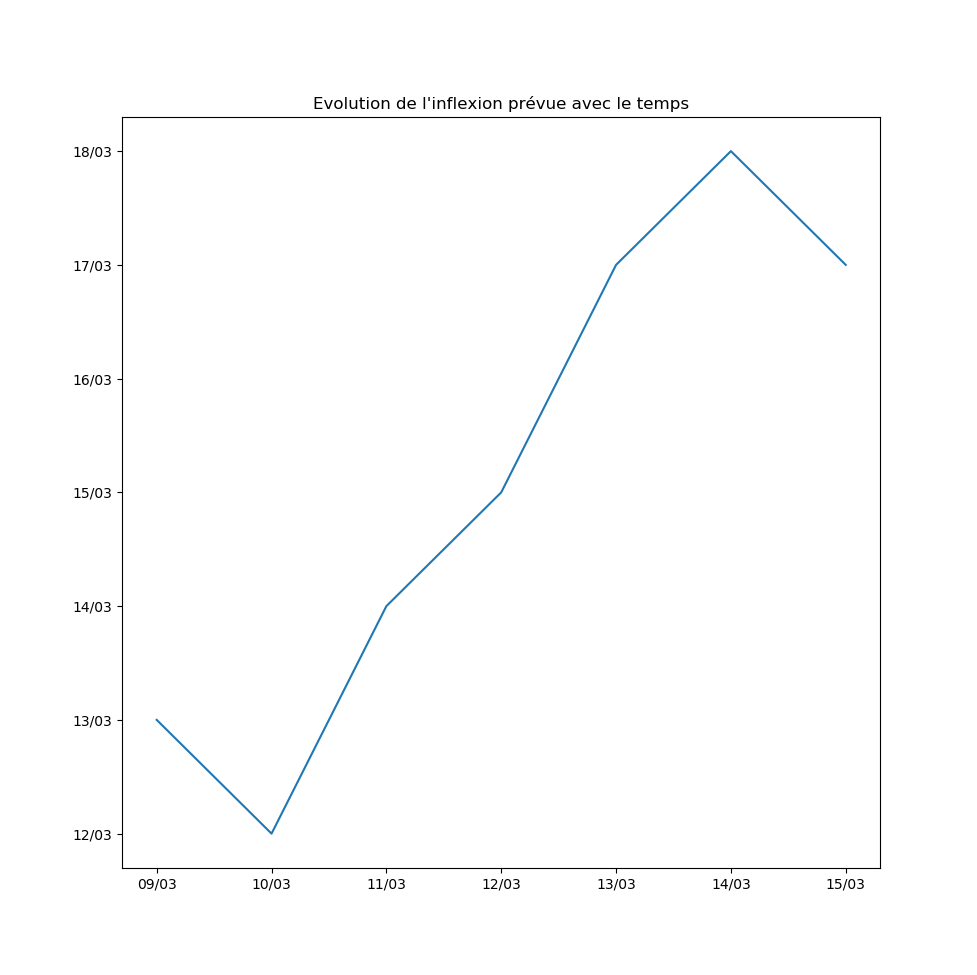
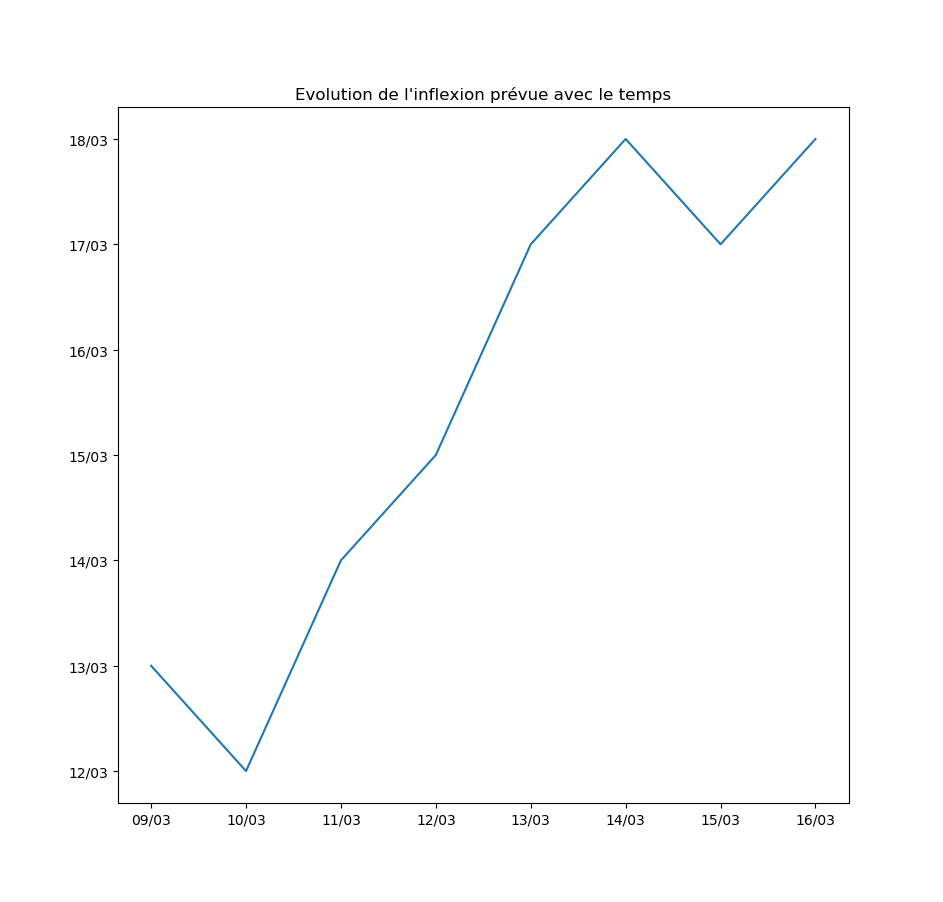
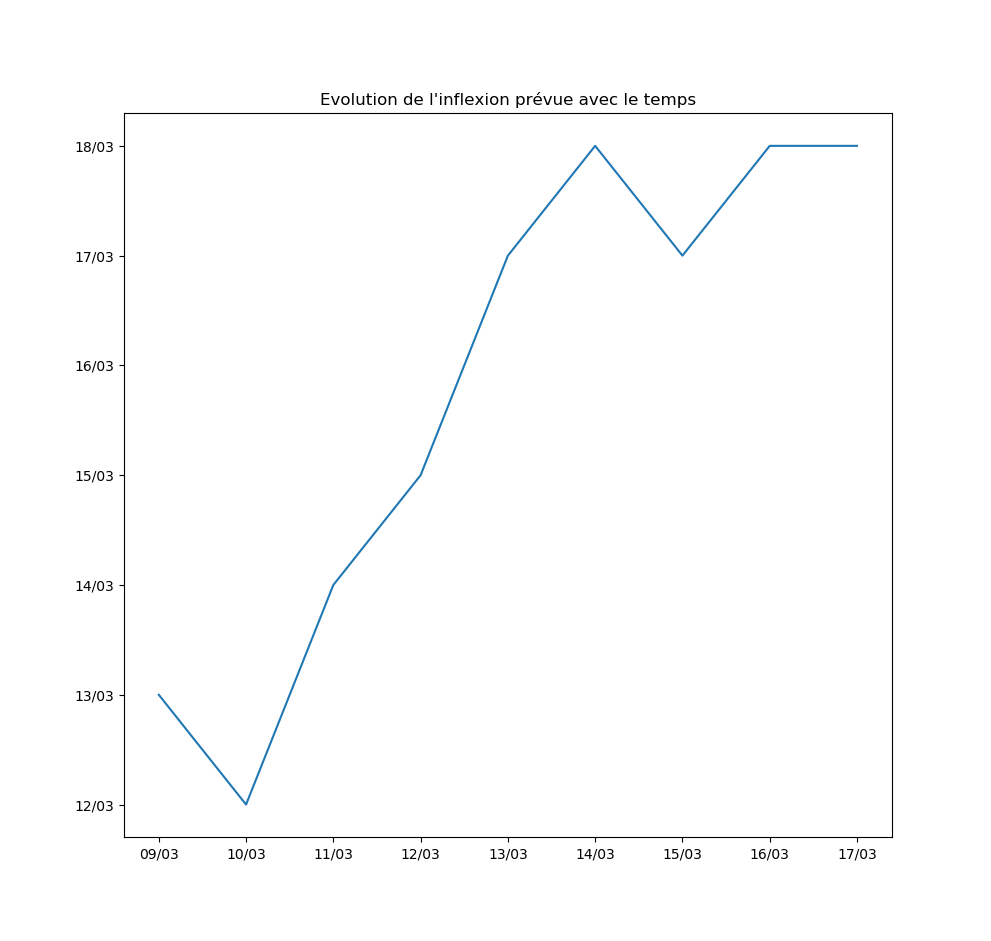
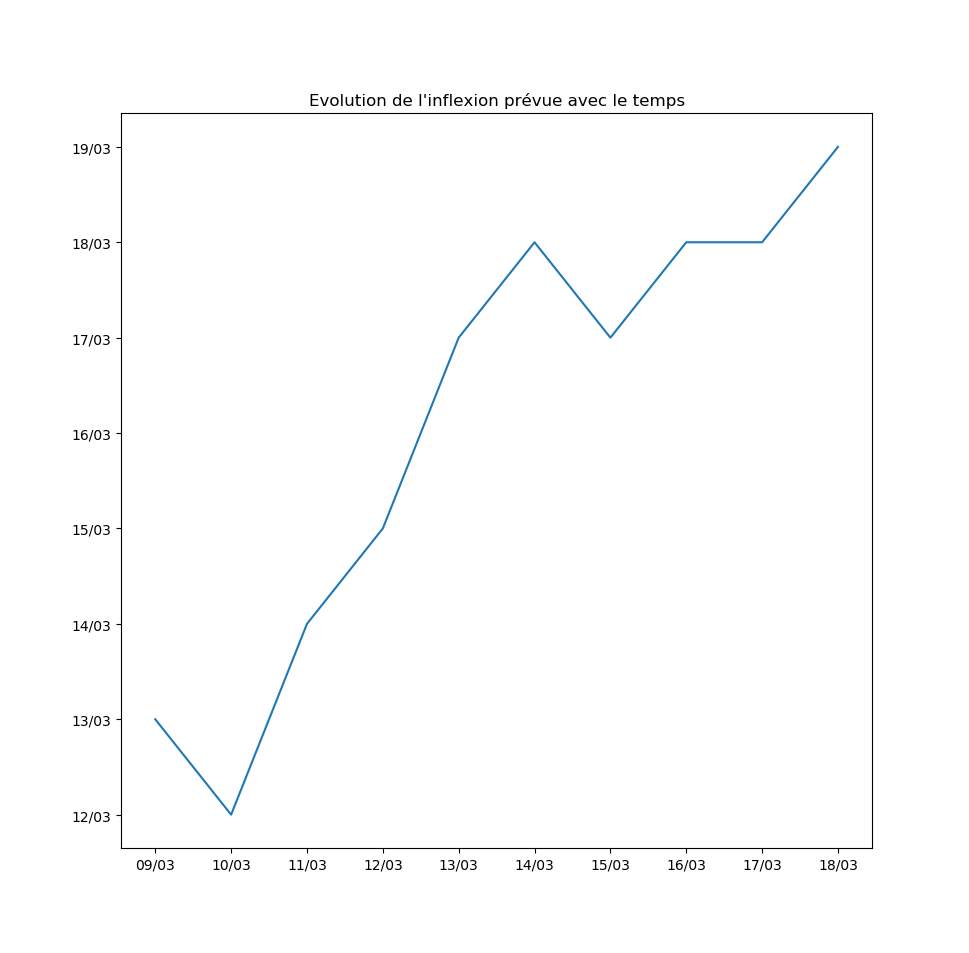
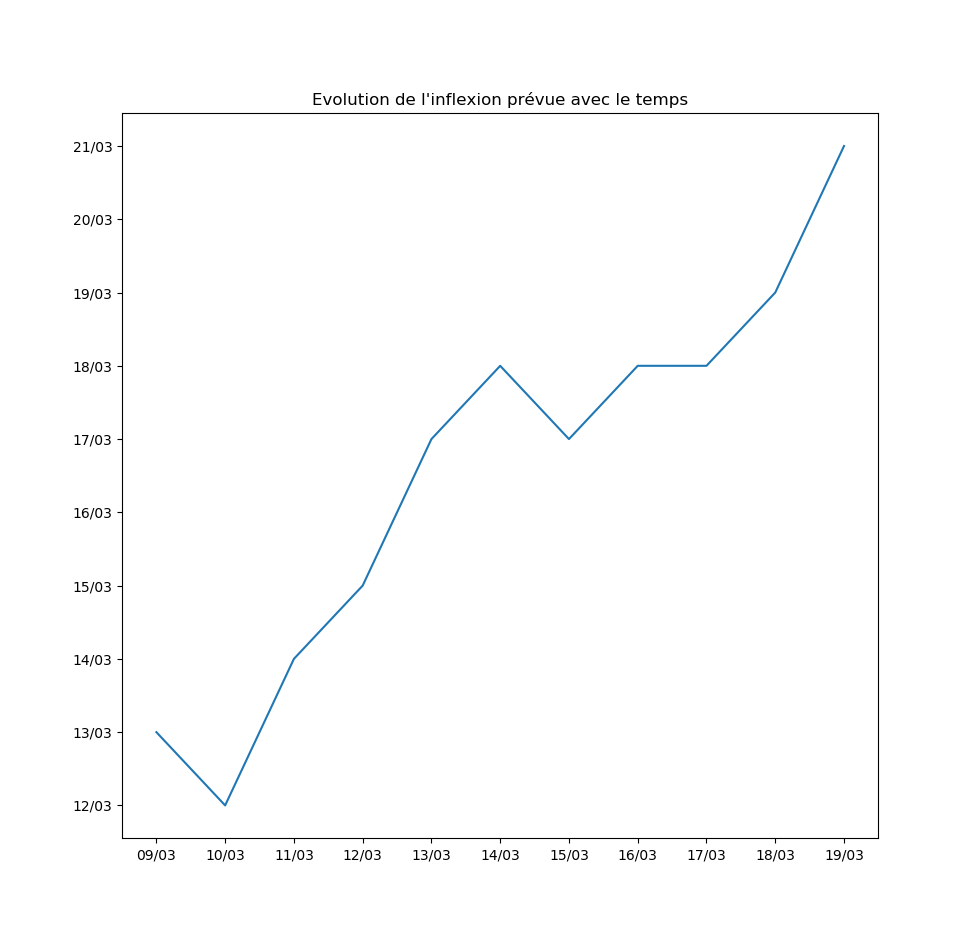
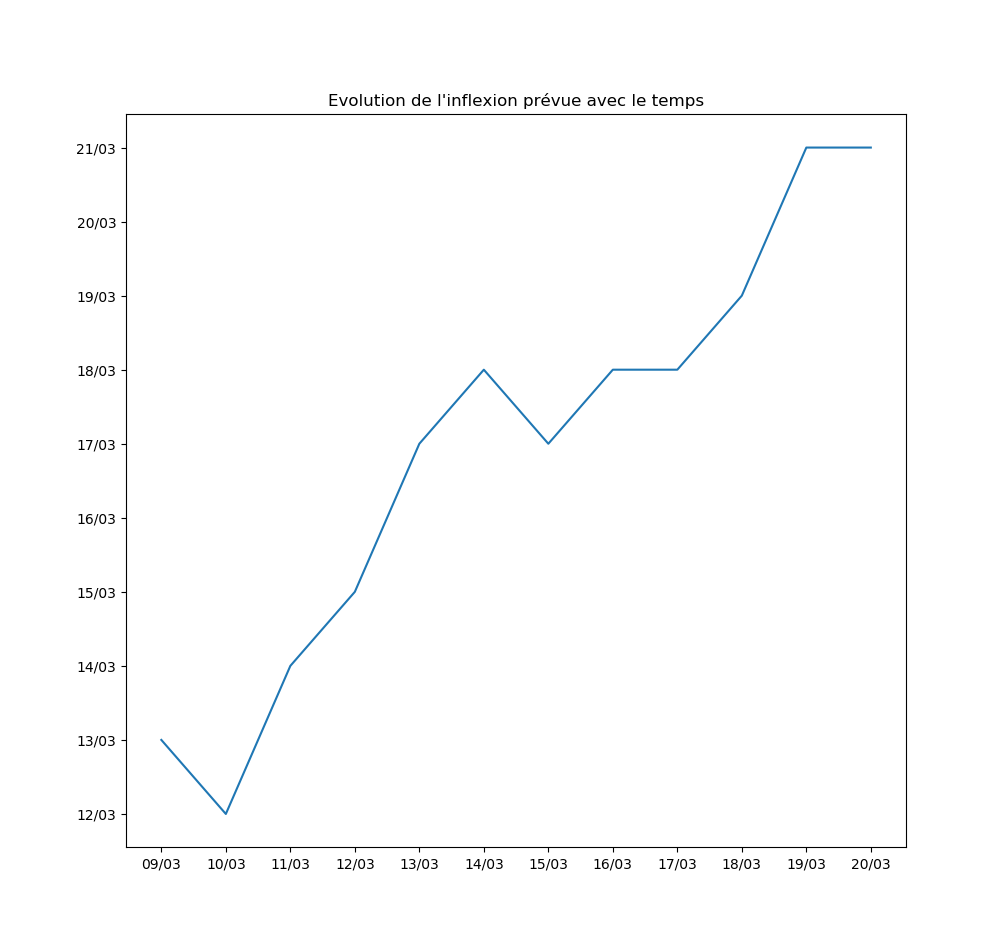
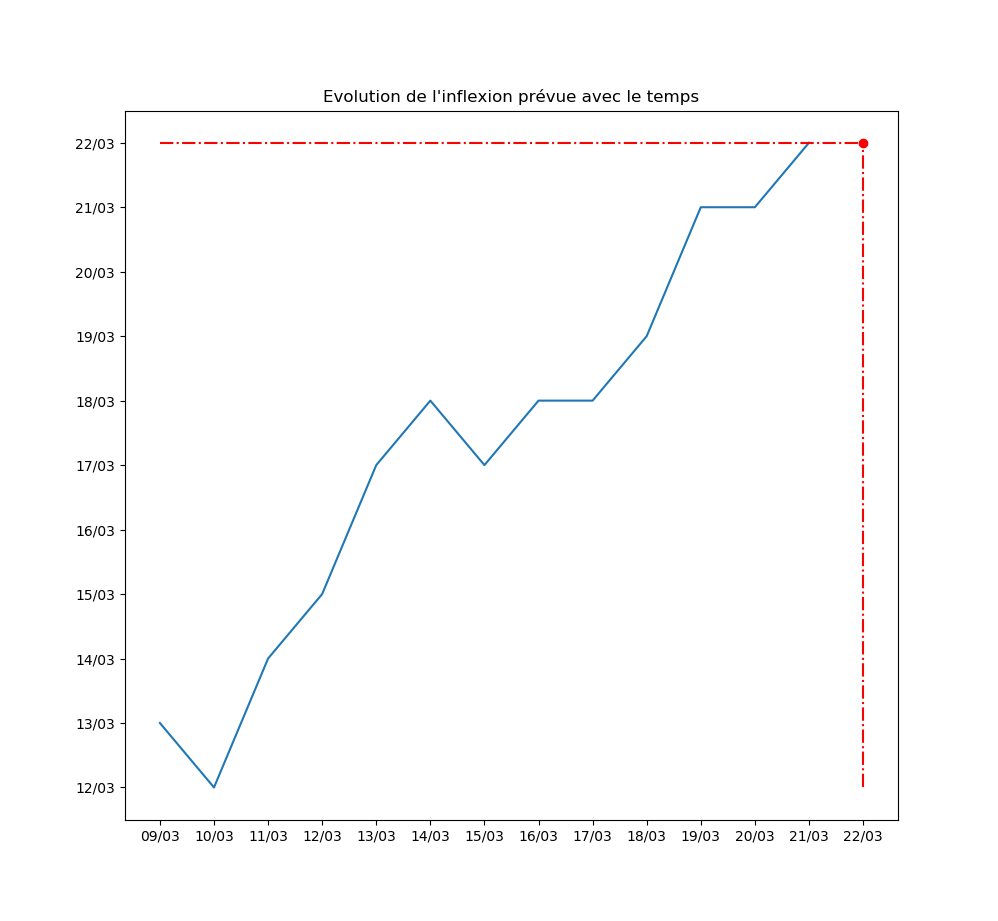
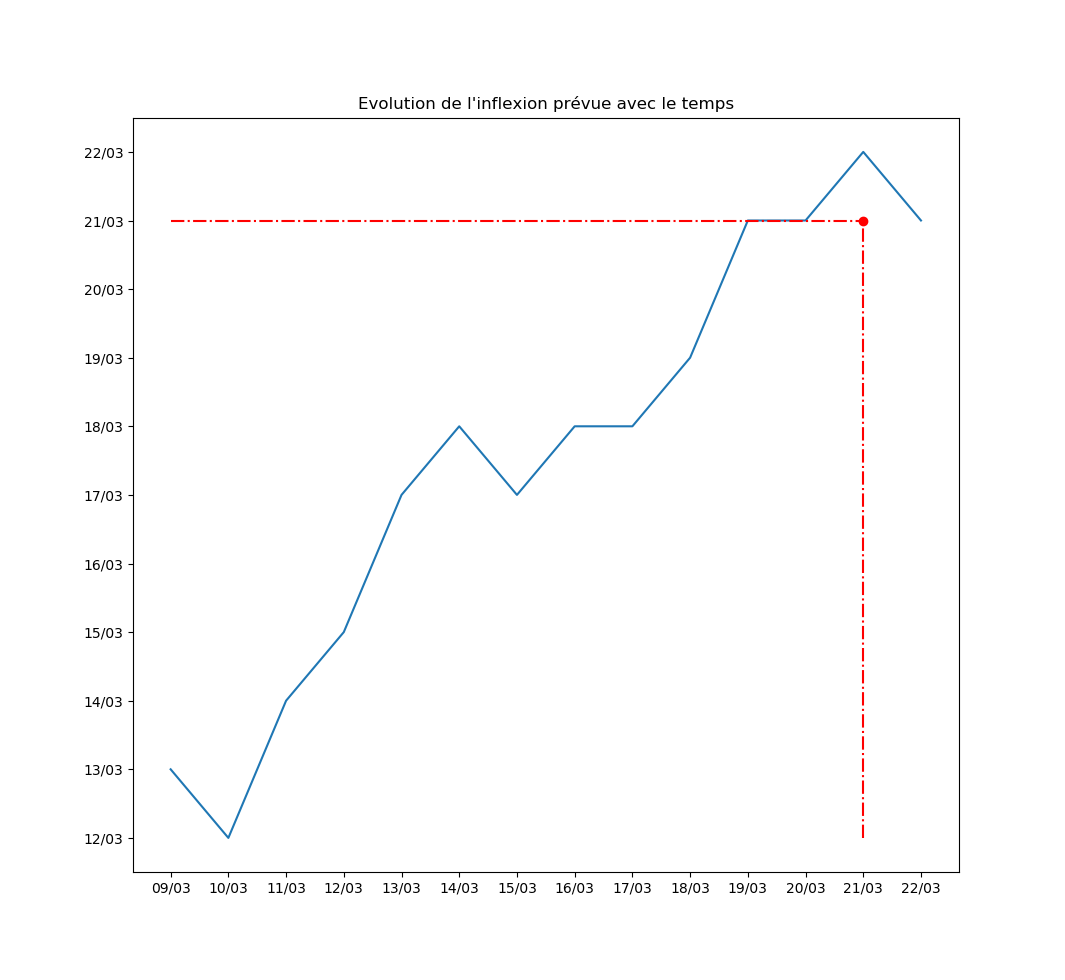
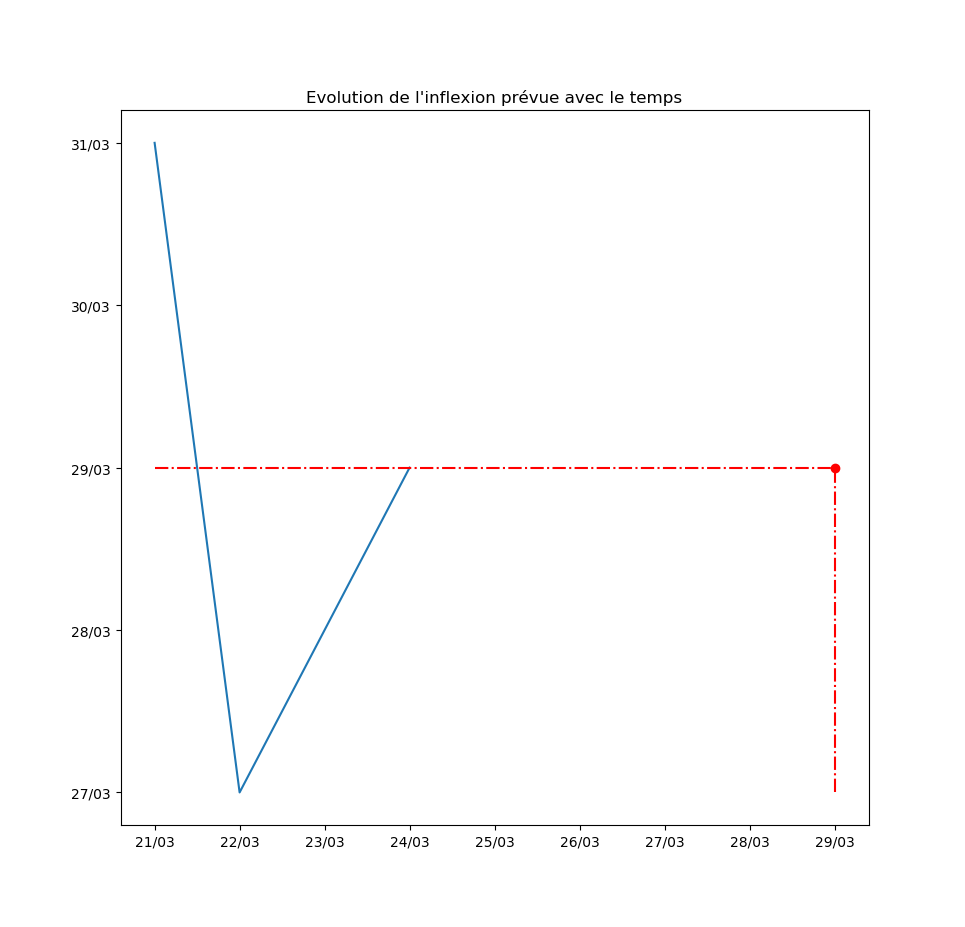
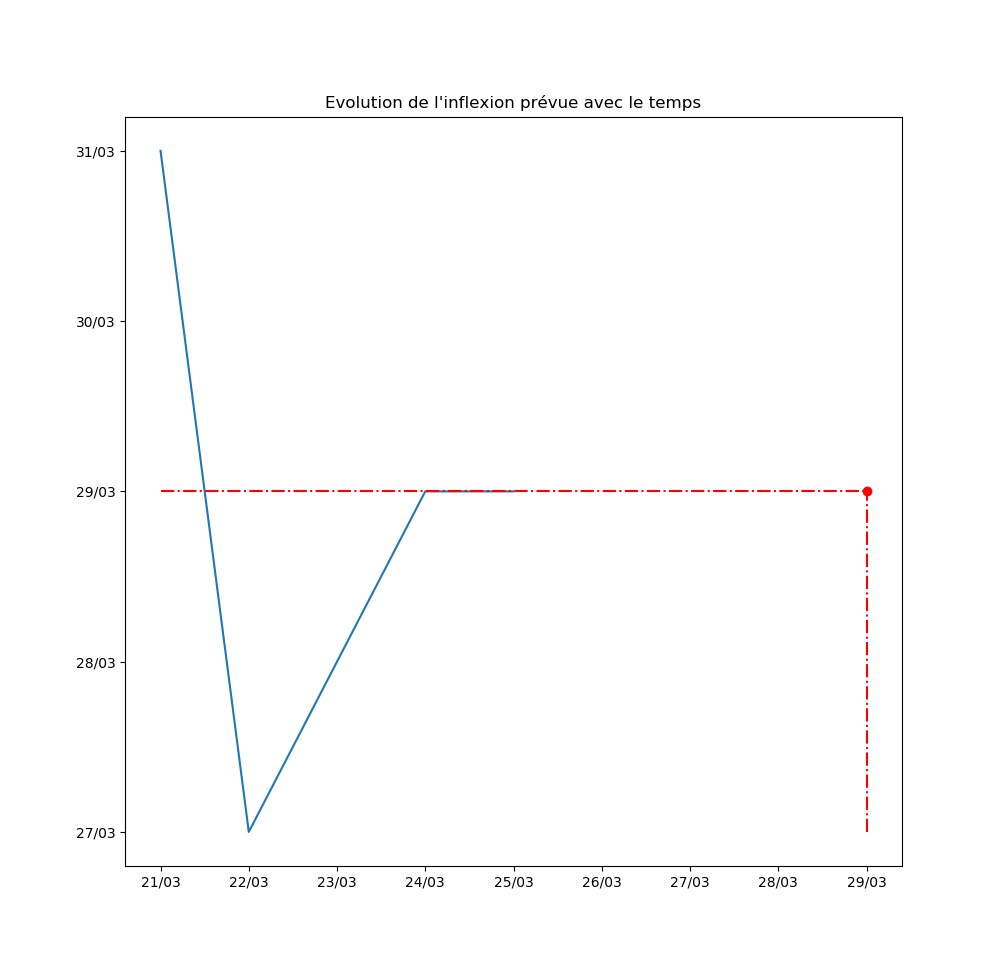
Autre exemple : la prévision par l’algorithme du jour d’inflexion de la courbe. Pour l’instant, l’inflexion est repoussée au moins d’un jour par jour… Ce qui signifie que le modèle ne voit aucune amélioration de la situation avec le temps.
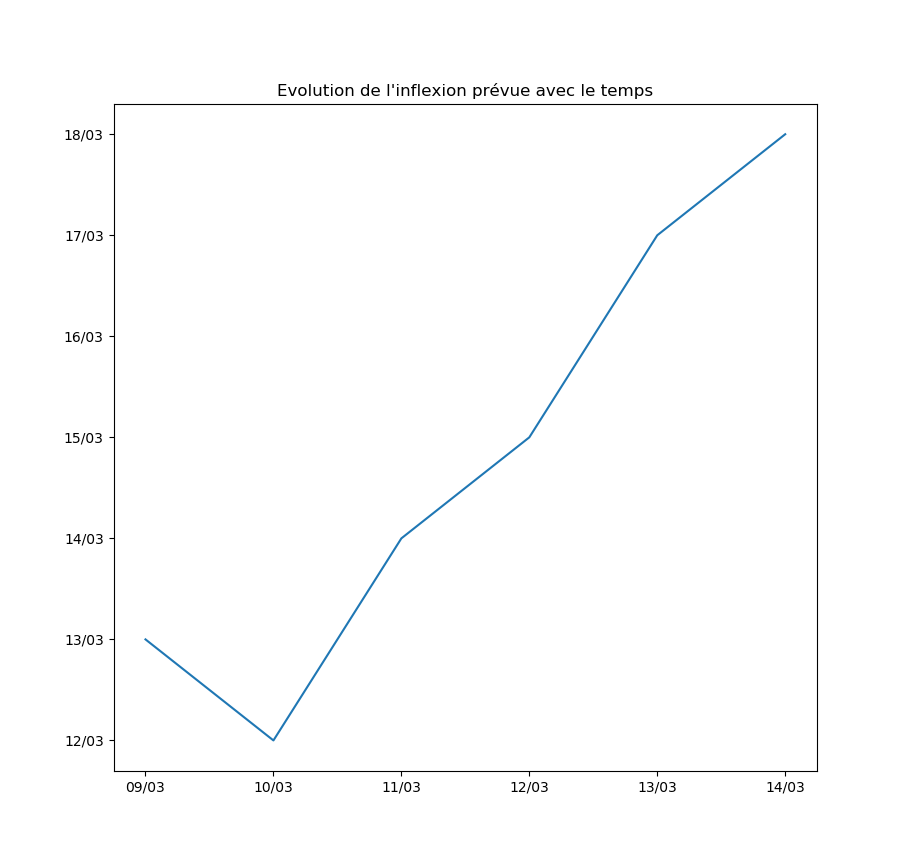
Conclusion
Je le répète : ce modèle est rudimentaire et purement mathématique. Il ne prétend pas décrire la complexité de la contagion par le SARS-CoV-19 en France. Notamment, il ne repose sur aucune base biologique et n’entre dans aucun détail géographique.
En revanche, il peut constituer un outil relativement fiable d’observation de l’efficacité des mesures de confinement. A cette fin, je mettrai à jour quotidiennement les graphiques présentés ci-dessus.
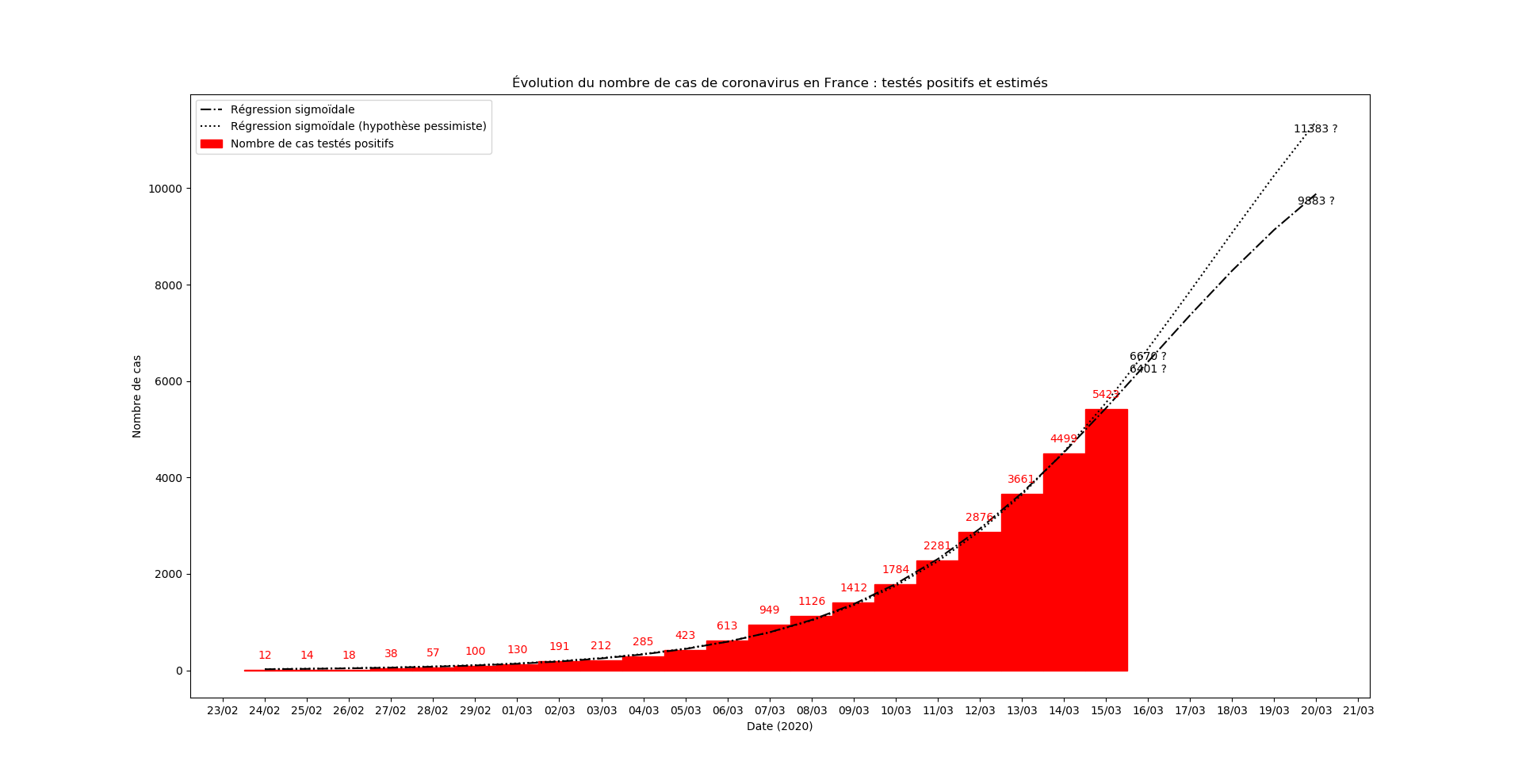
Une prévision du nombre de nouveaux cas le 15 mars au soir :
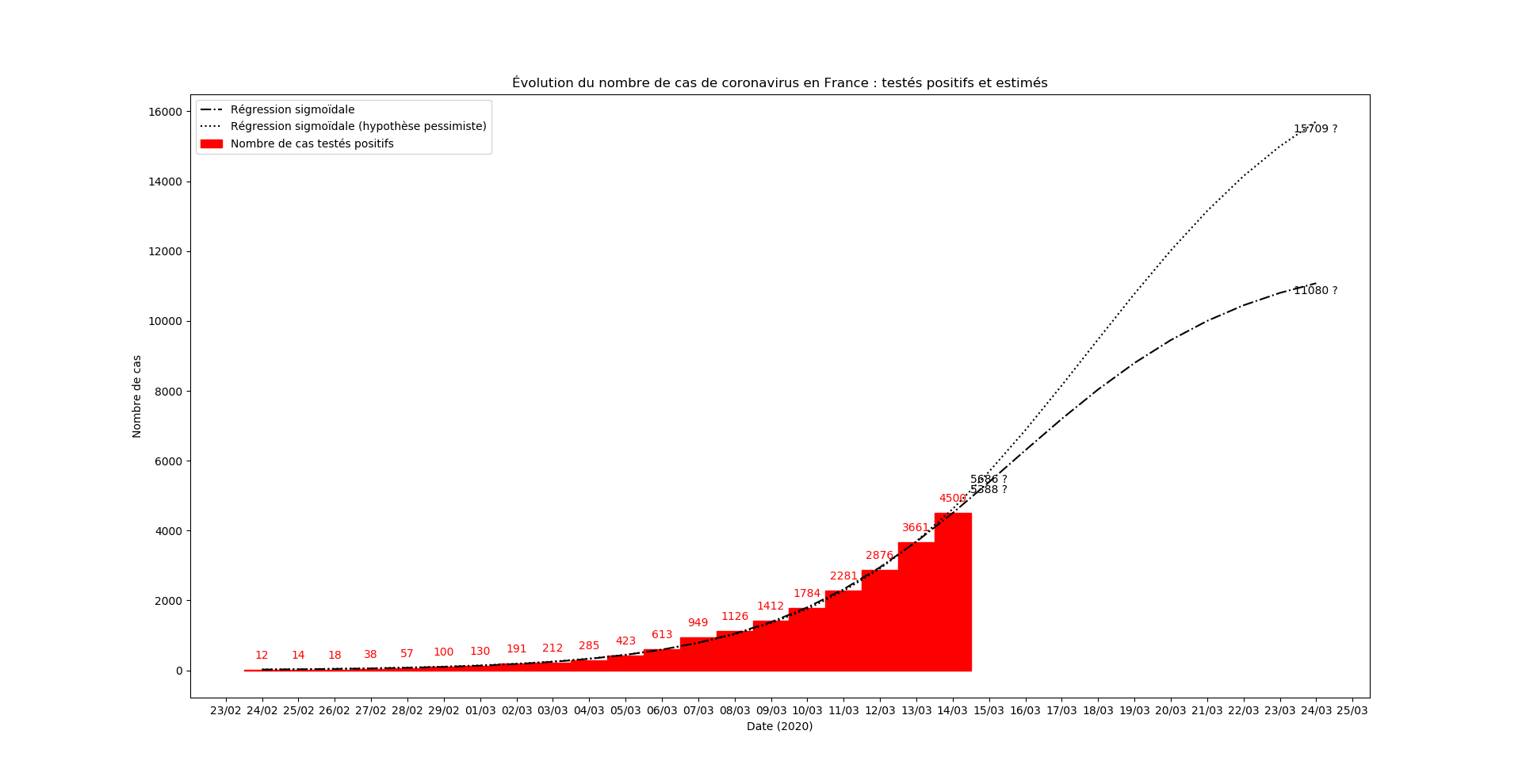
Deux articles (en anglais) pour finir, où des simulations permettent de mieux comprendre l’enjeu des mesures de restriction imposées ces derniers jours : Washington Post et Vox.com.
Mise-à-jour du 15 mars au soir
Légère amélioration de la situation par rapport à hier.
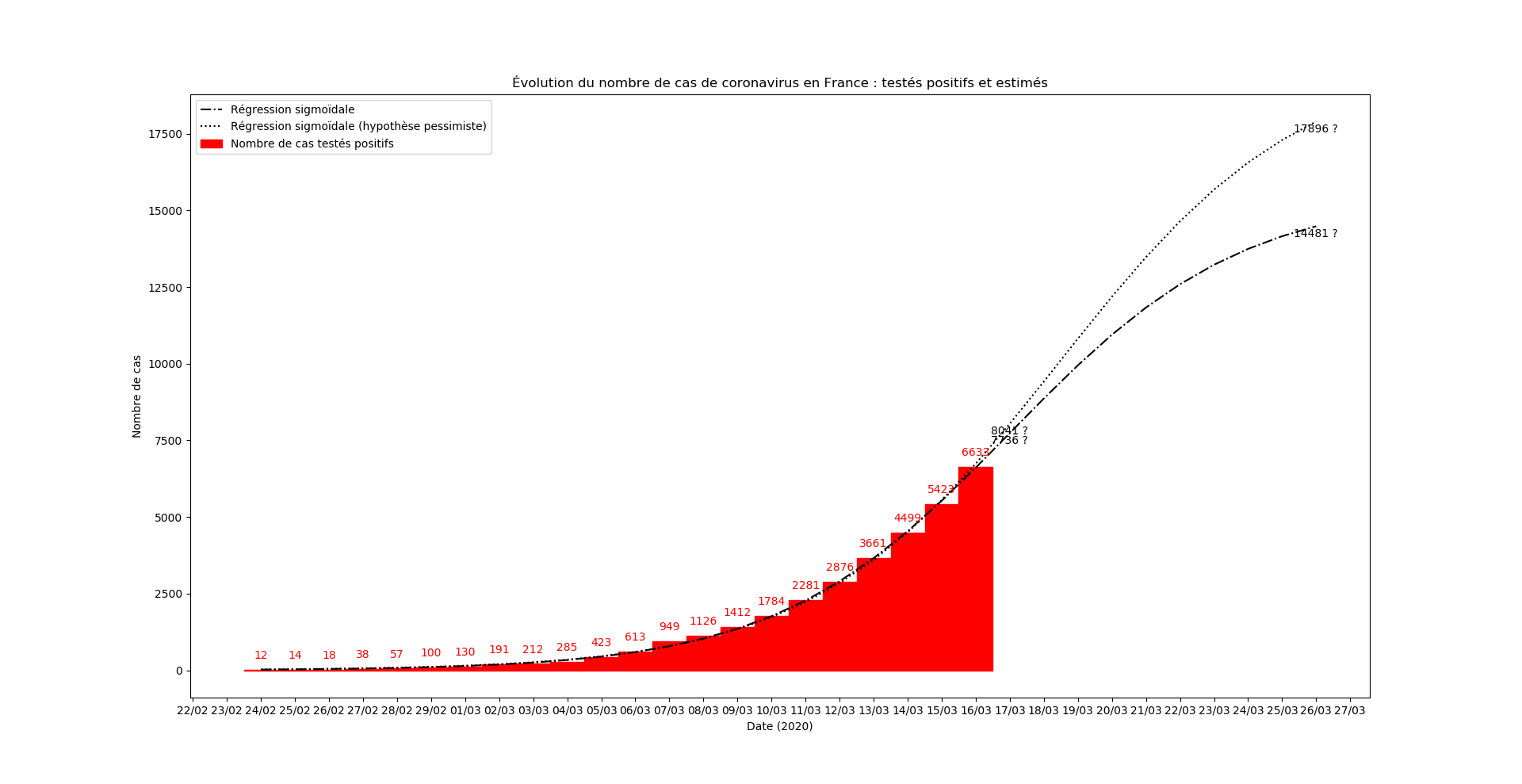
Mise-à-jour du 16 mars au soir
Ça repart à la hausse…
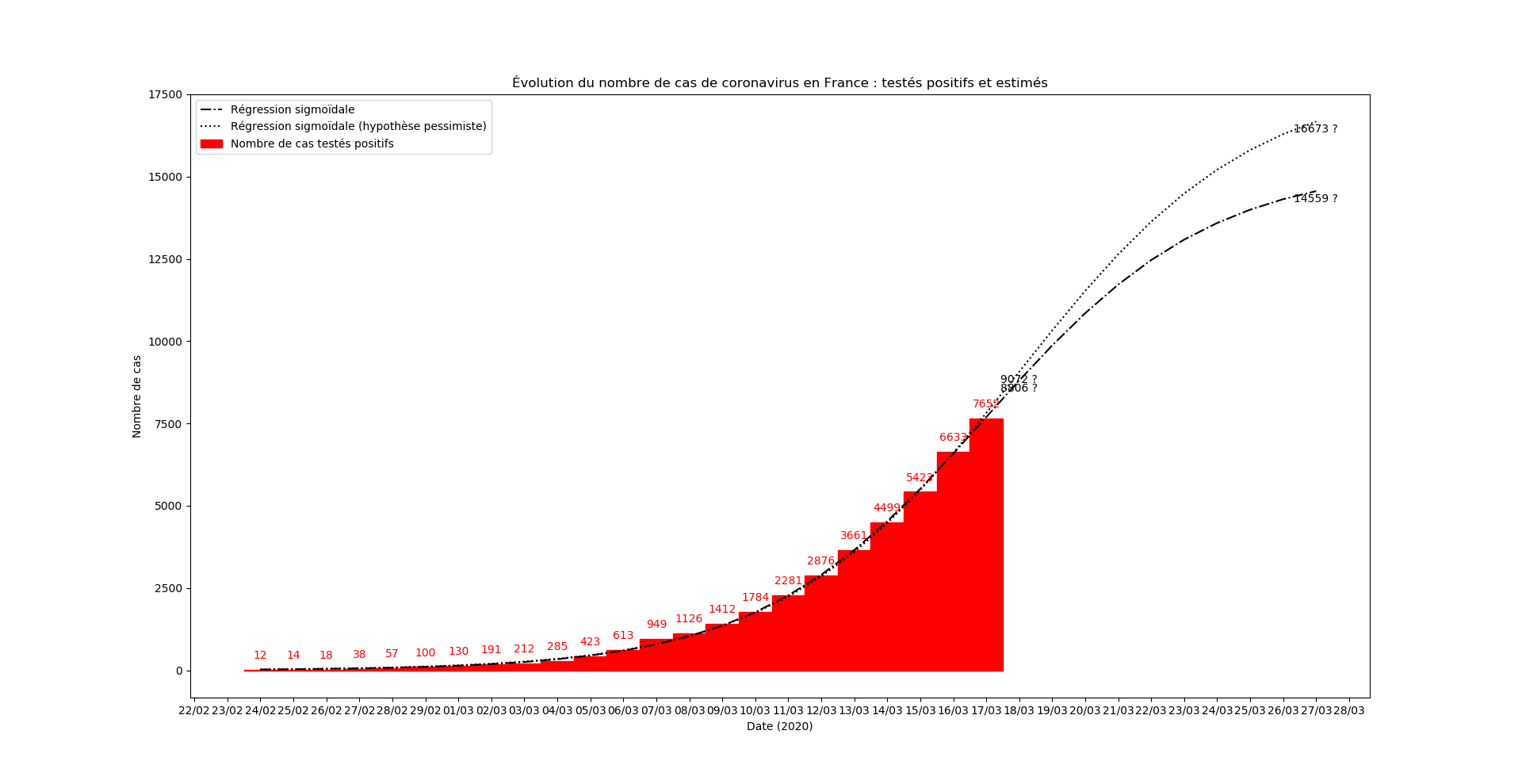
Mise-à-jour du 17 mars au soir
Oh oh oh ! Le nombre réel de cas testés positifs est inférieur à la prévision du modèle !
C’est la première fois et c’est bon signe…
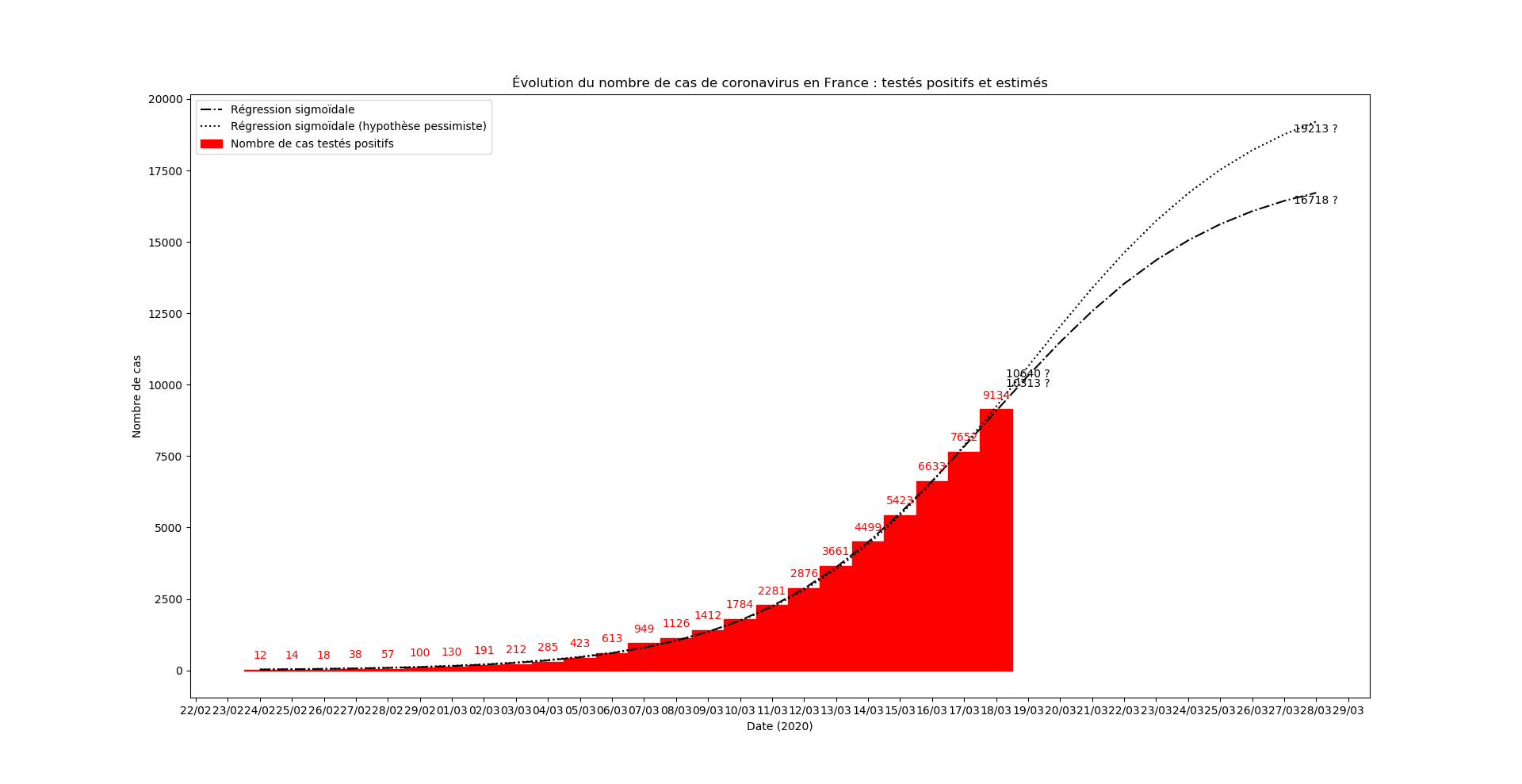
Mise-à-jour du 18 mars au soir
La douche froide
Mise-à-jour du 19 mars au soir
Déprimant
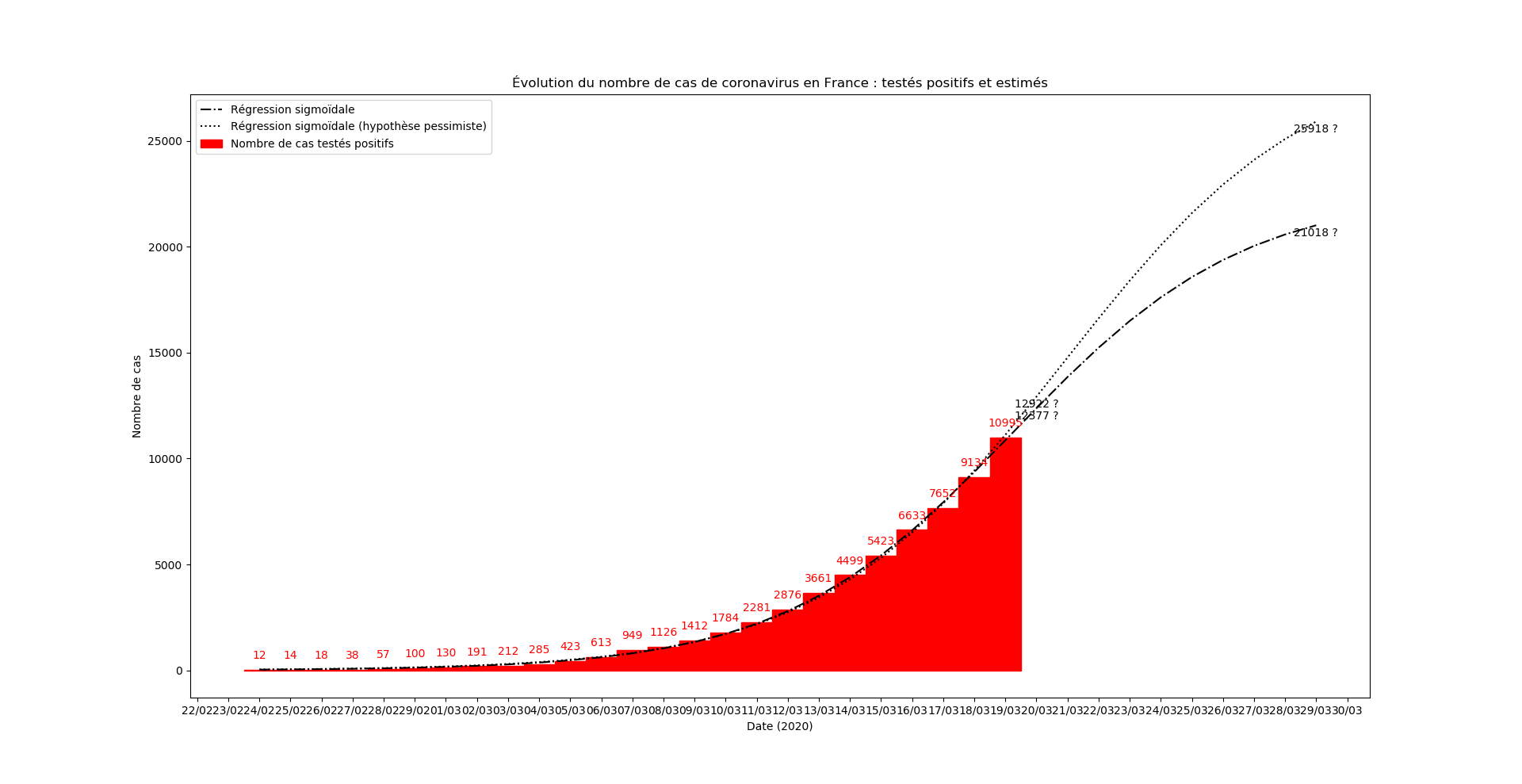
Mise-à-jour du 20 mars au soir
Sans commentaire
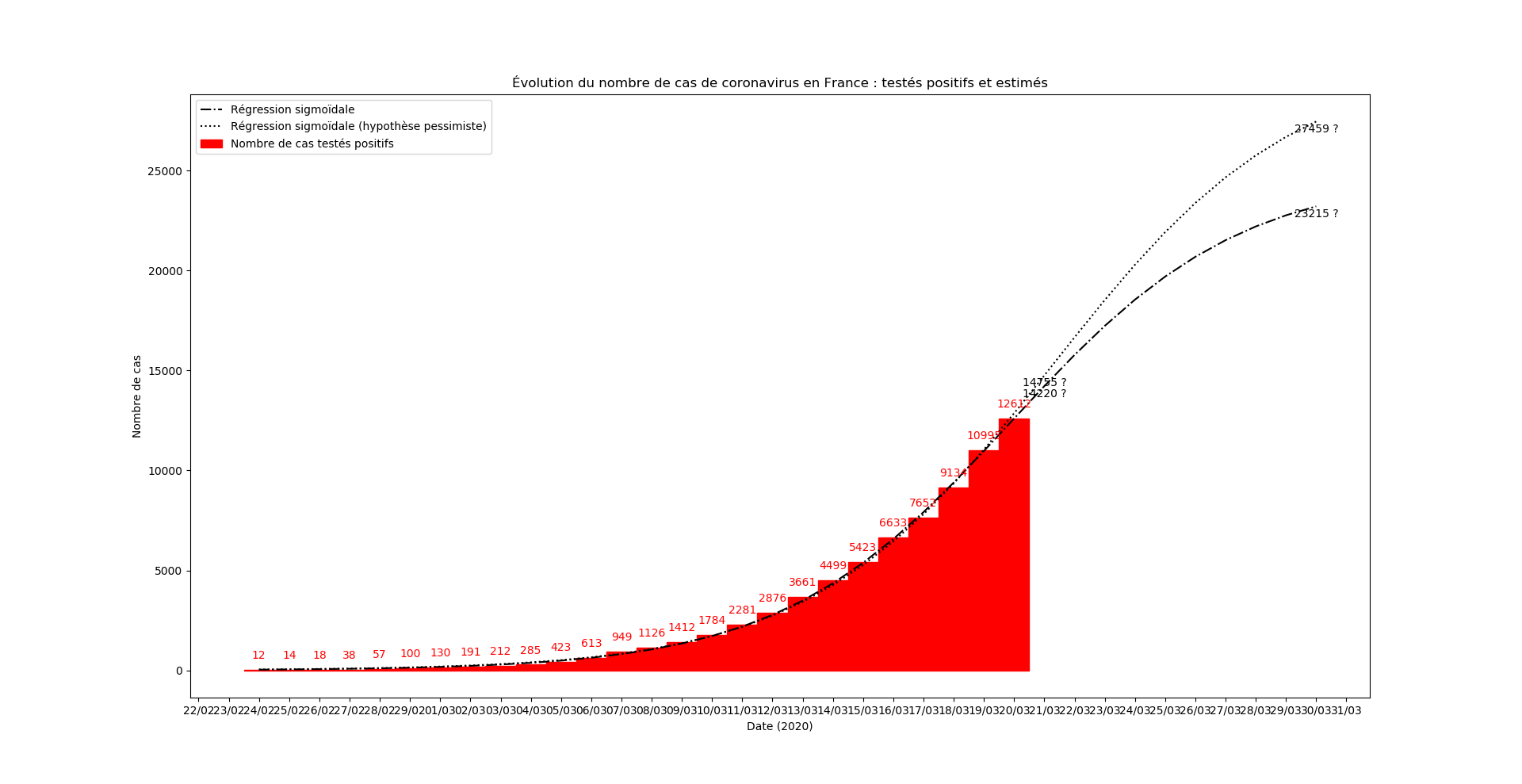
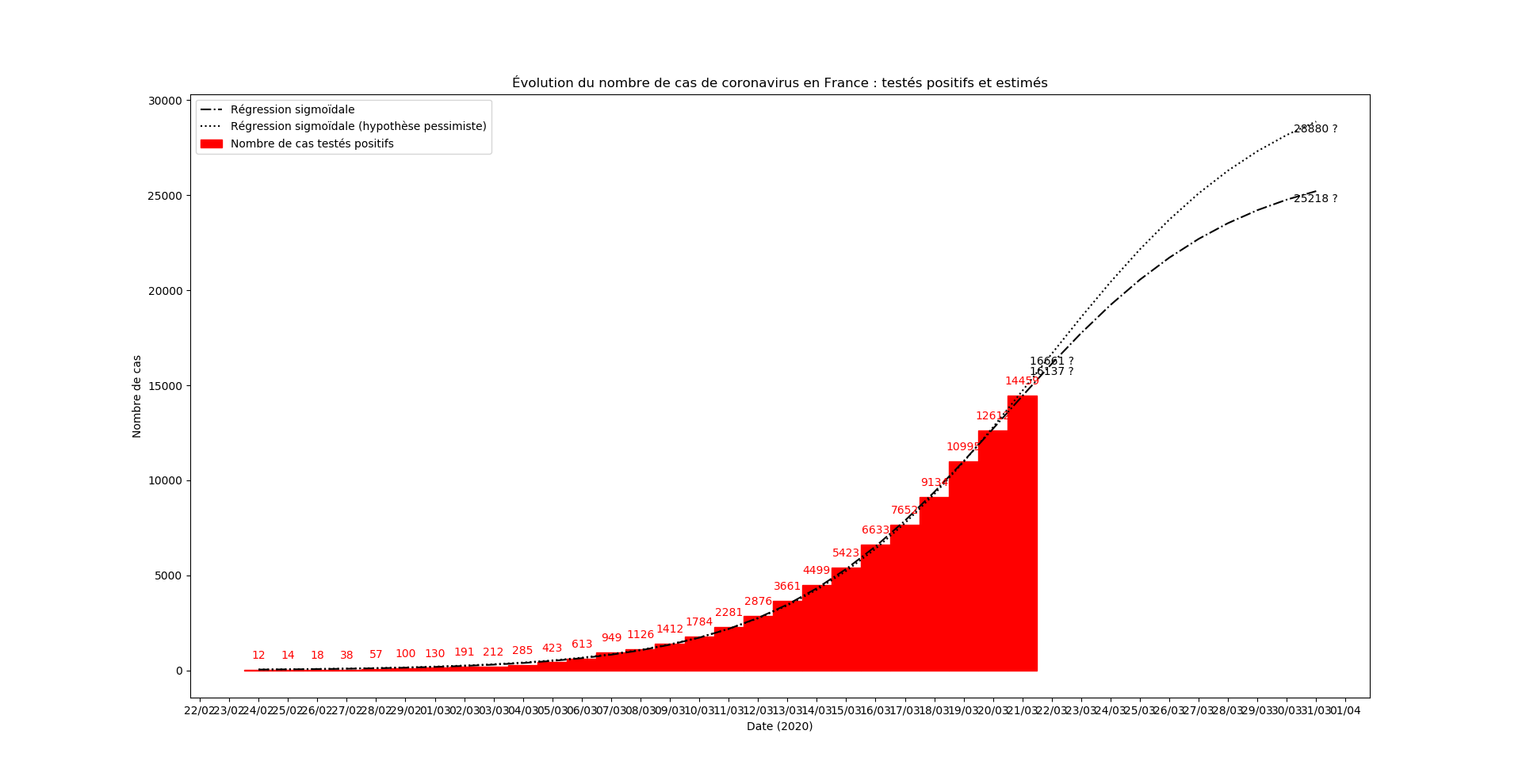
Mise-à-jour du 21 mars au soir
Inflexion en vue ?
Mise-à-jour du 22 mars au soir
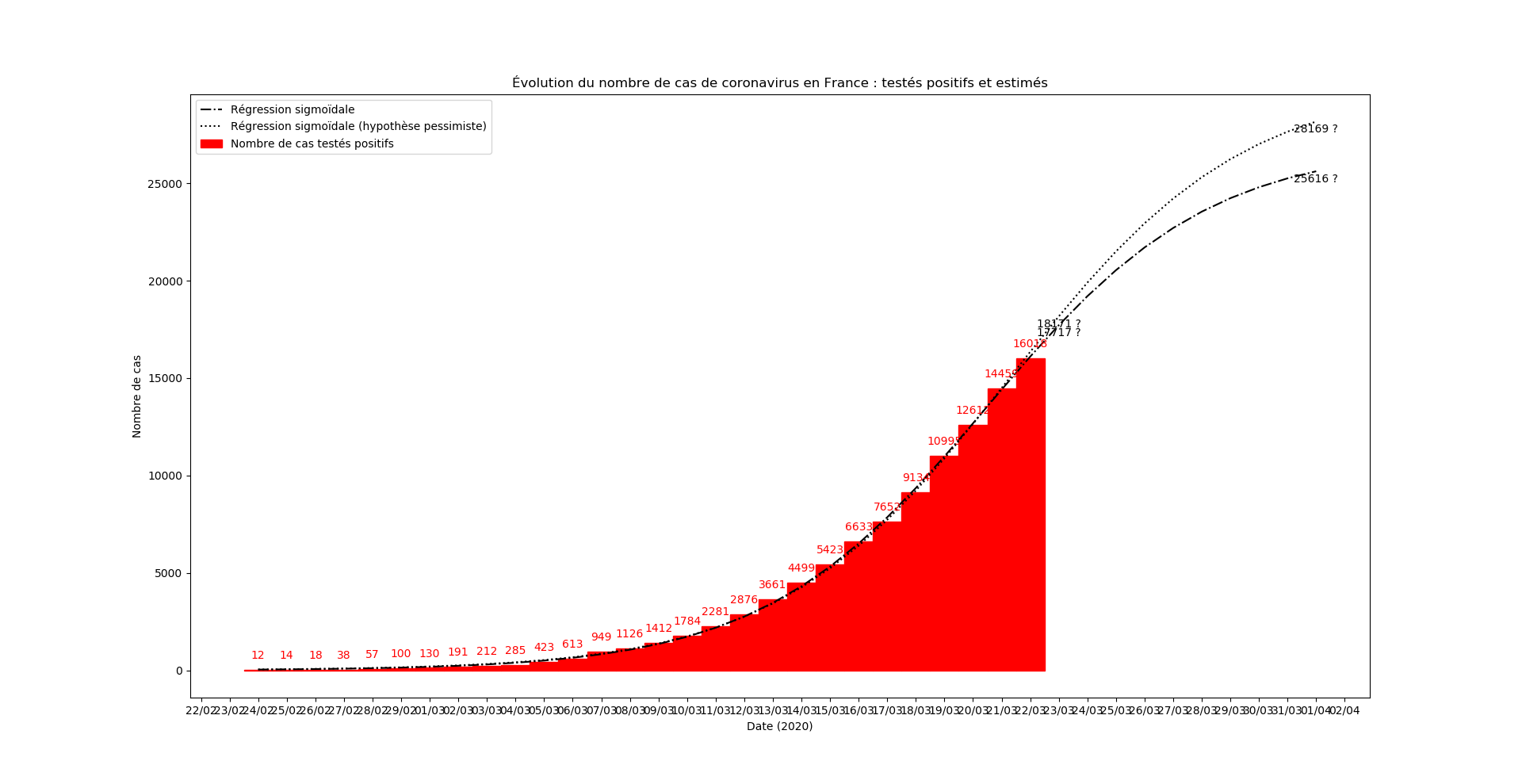
Avec toutes les précautions d’usage… l’inflexion est derrière nous ! On reste confinés, on déconne pas.
Mais il y a plusieurs choses très positives ce soir :
- l’inflexion, donc, est datée d’hier selon la simulation. Autrement dit, le nombre de nouveaux cas testés positifs devrait désormais diminuer chaque jour davantage.
- le nombre de nouveaux cas donnés par la simulation est surévalué ce qui pourrait être l’un des premier signes visibles de la politique de confinement.
- et une dernière chose, si effectivement l’inflexion est passée, et si le modèle sigmoïdal est adapté, alors la simulation devrait désormais devenir très robuste et ses paramètres devraient converger… À voir.
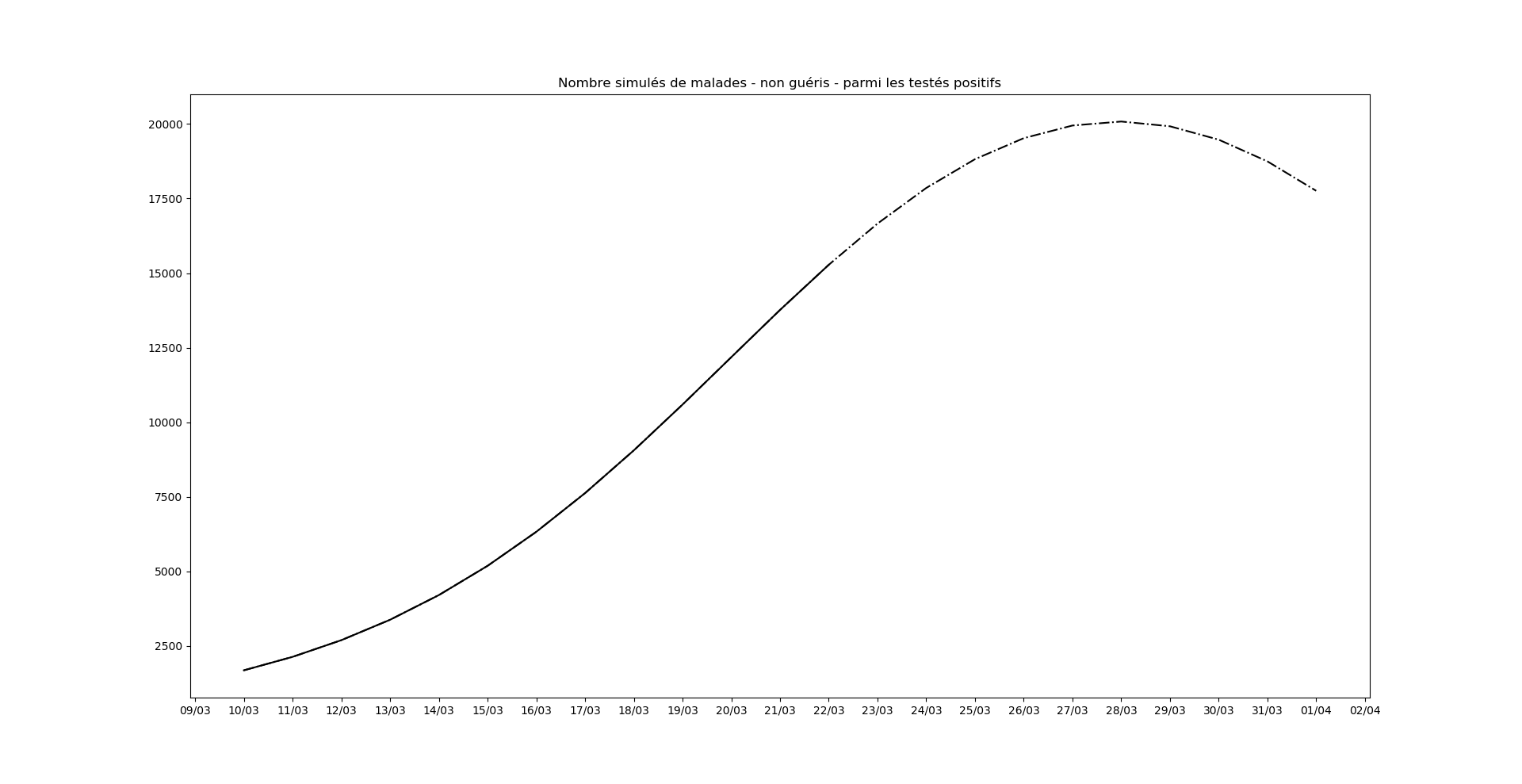
Enfin, une nouveauté : je donne aussi une simulation du nombre de gens malades (parmi les testés positifs) qui fait apparaître un pic épidémique pour le 28 mars…
Mise-à-jour du 24 mars au soir
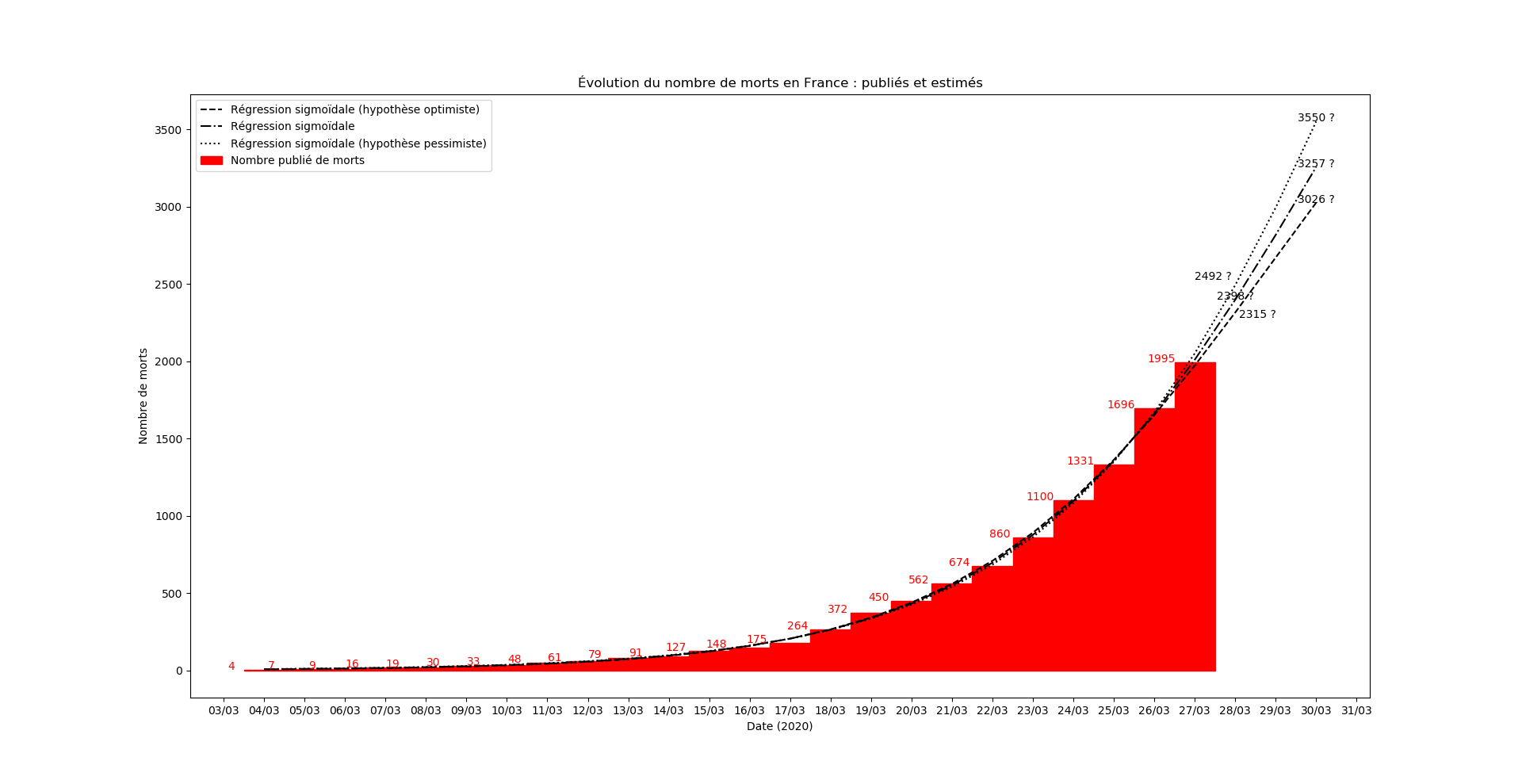
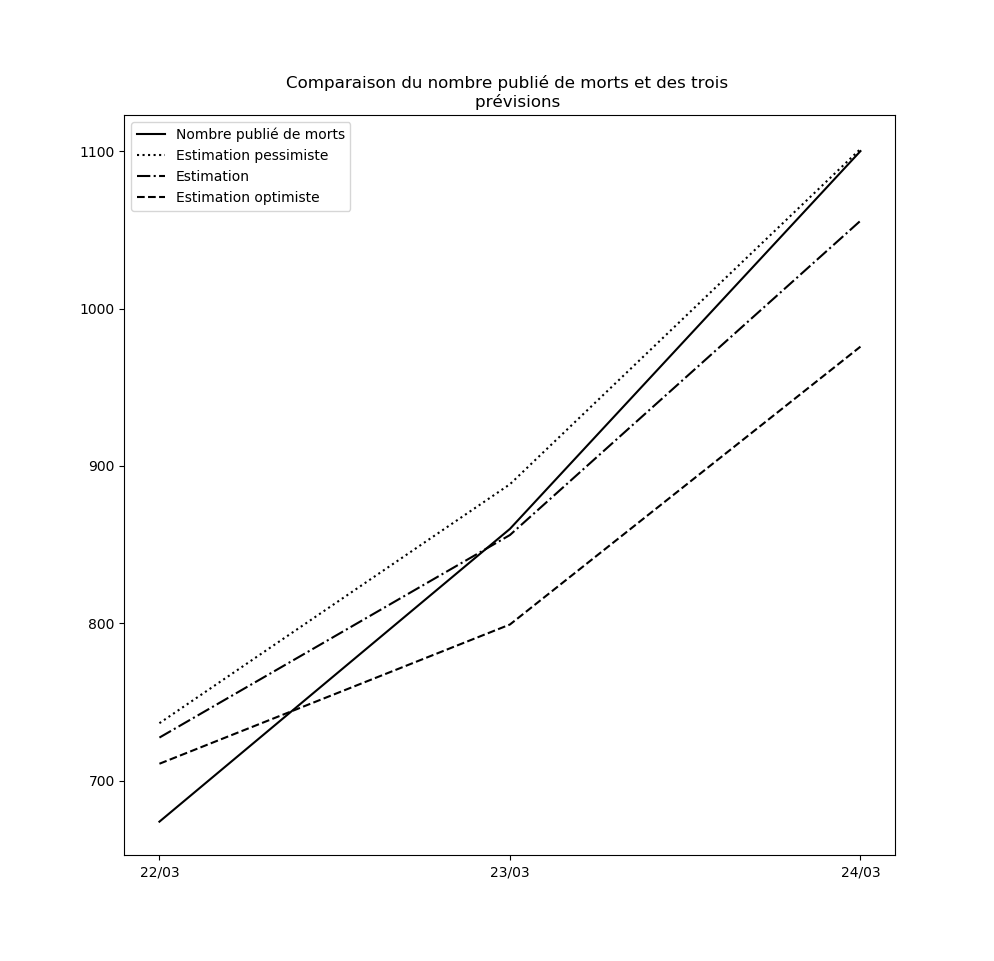
Le nombre de COVID+ étant devenu incohérent avec les données antérieures… je modélise désormais le nombre de morts. Au passage, j’ai aussi trouvé un raccourci pour mon algo, dès que j’ai le temps je publie un truc sur le sujet.
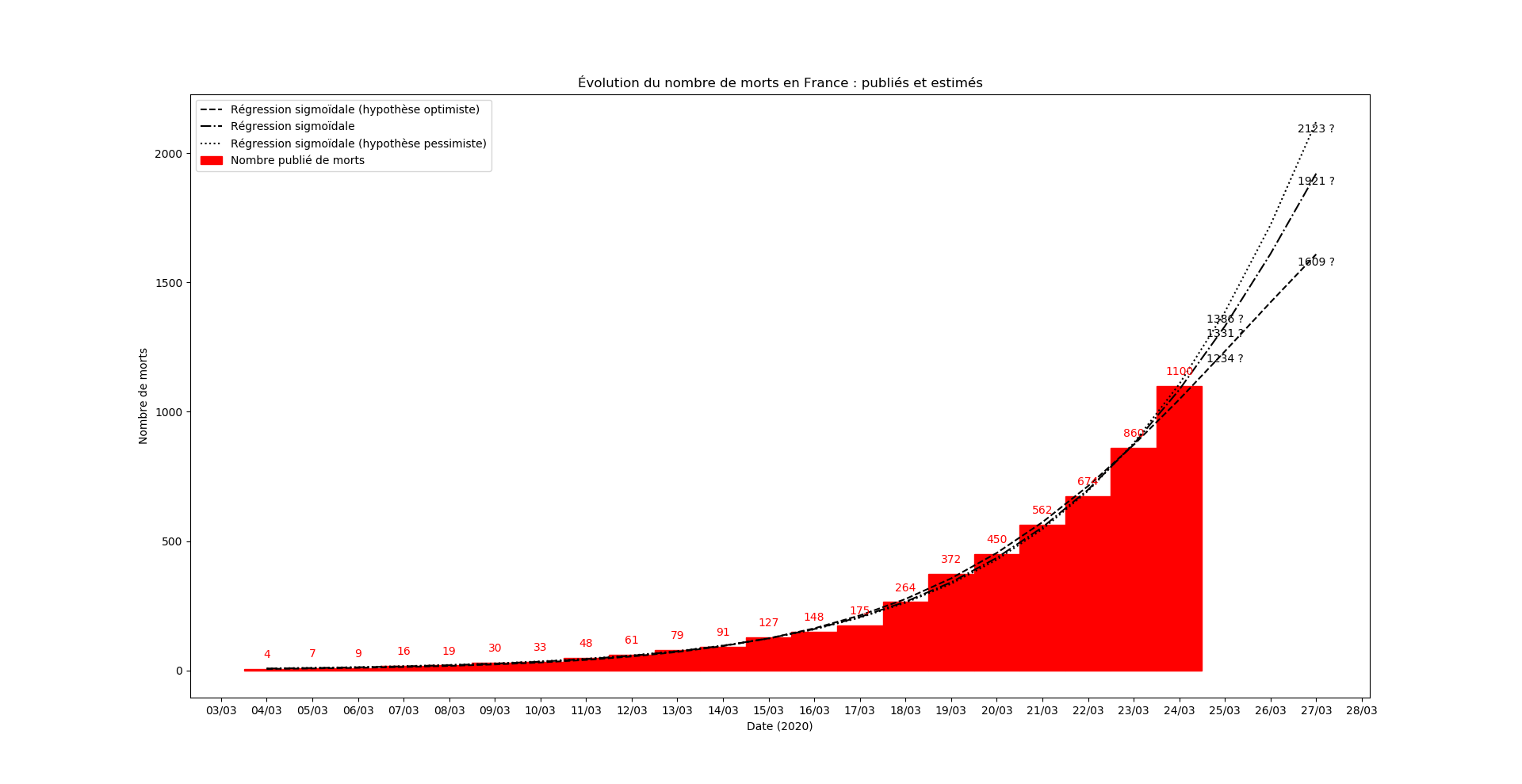
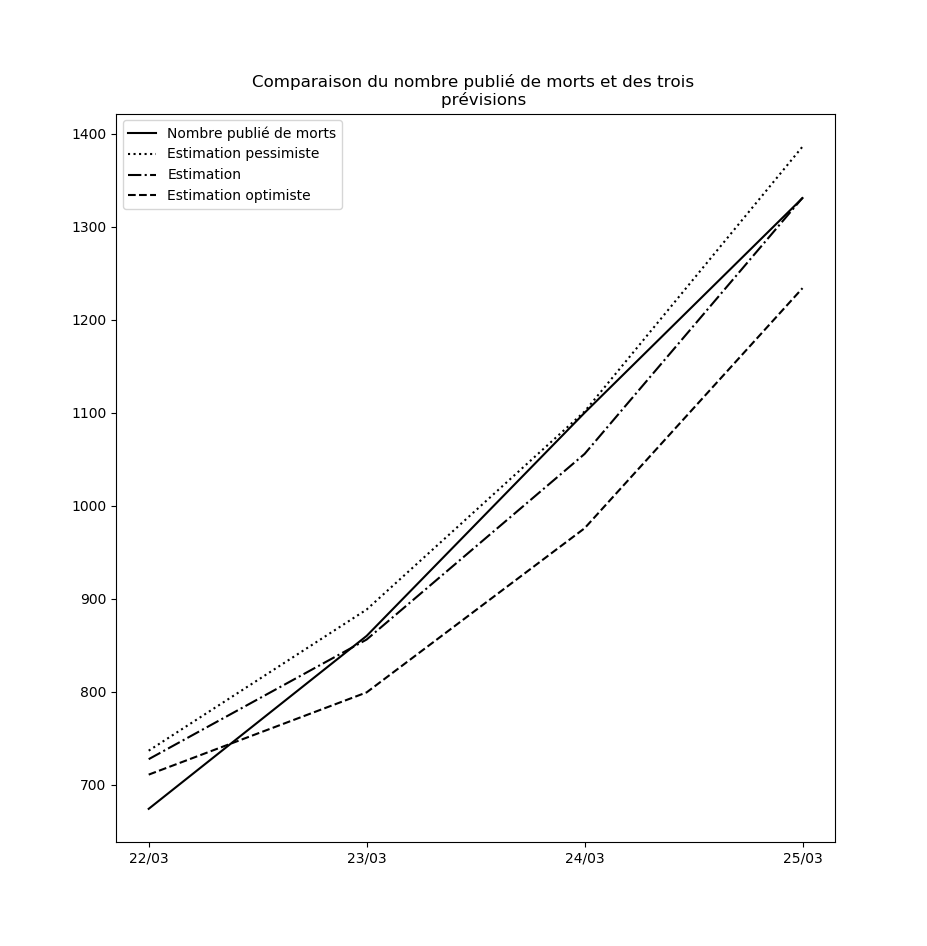
Mise-à-jour du 25 mars au soir
La prévision s’est avérée exacte aujourd’hui. C’est un hasard. Mais le modèle m’apparaît - de plus en plus - étonnamment valide. J’ai aussi continué à faire la modélisation du nombre de COVID+ et là aussi, après un jour erratique, le modèle se comporte étonnamment bien.
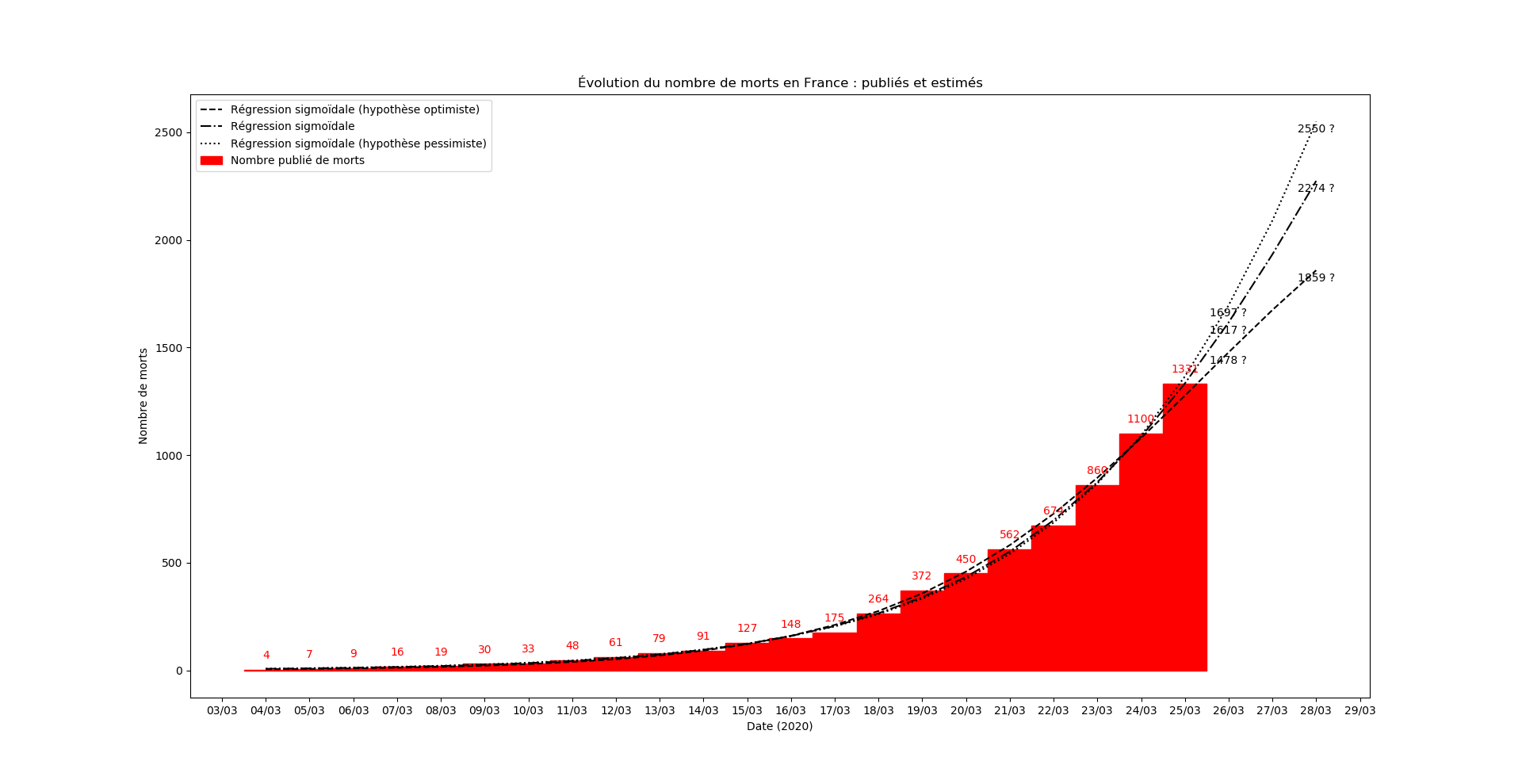
Mise-à-jour du 26 mars au soir
Oups, j’avais oublié les graphiques !
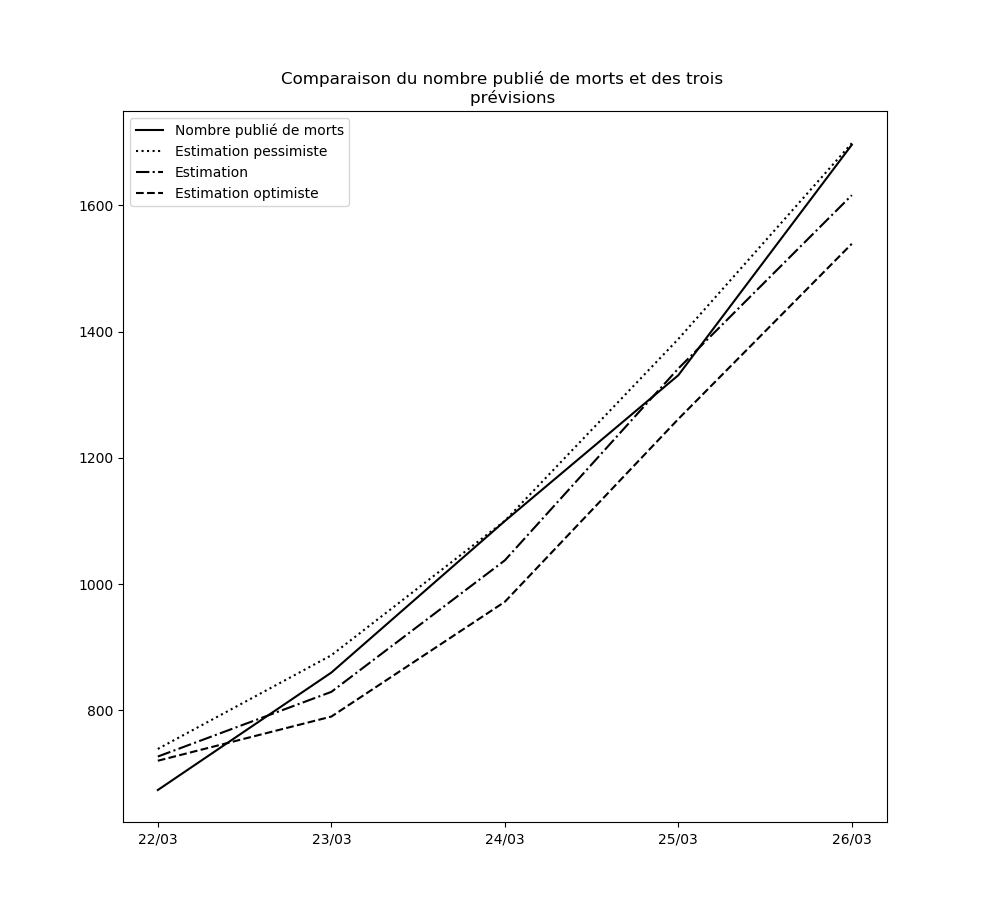
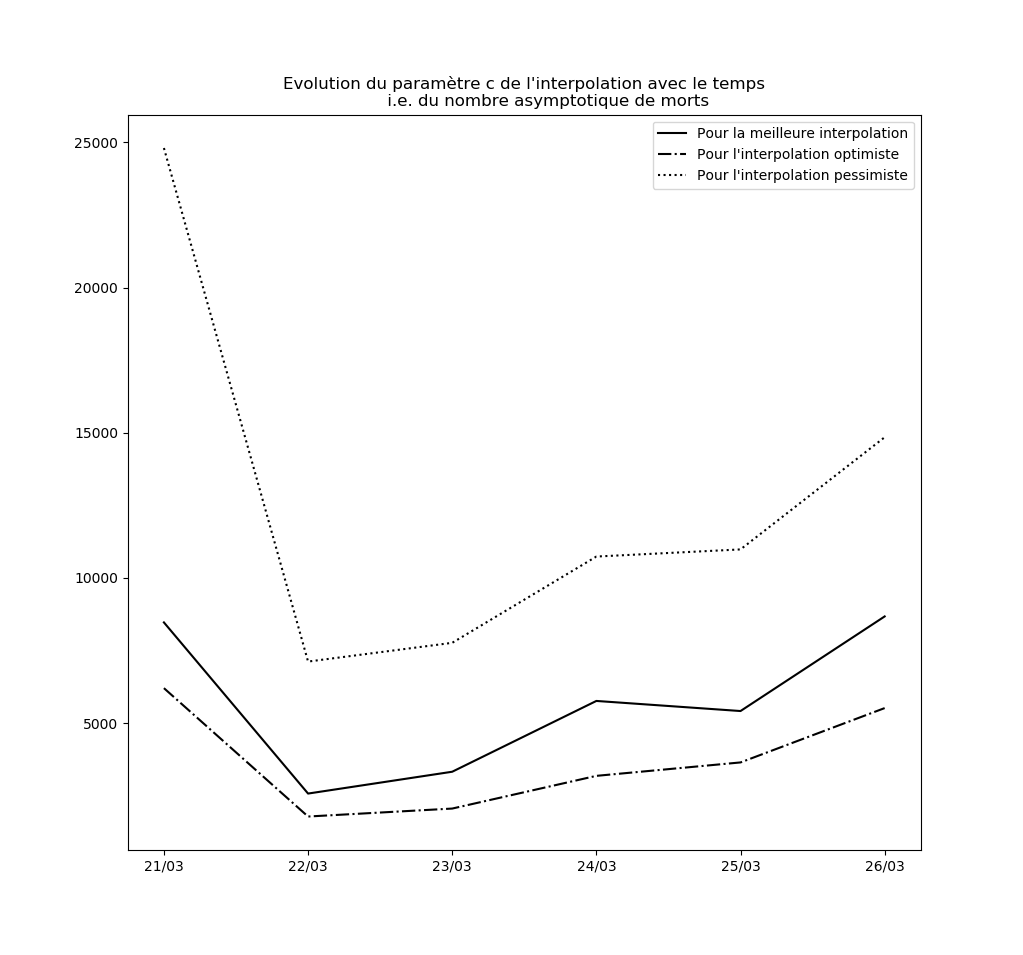
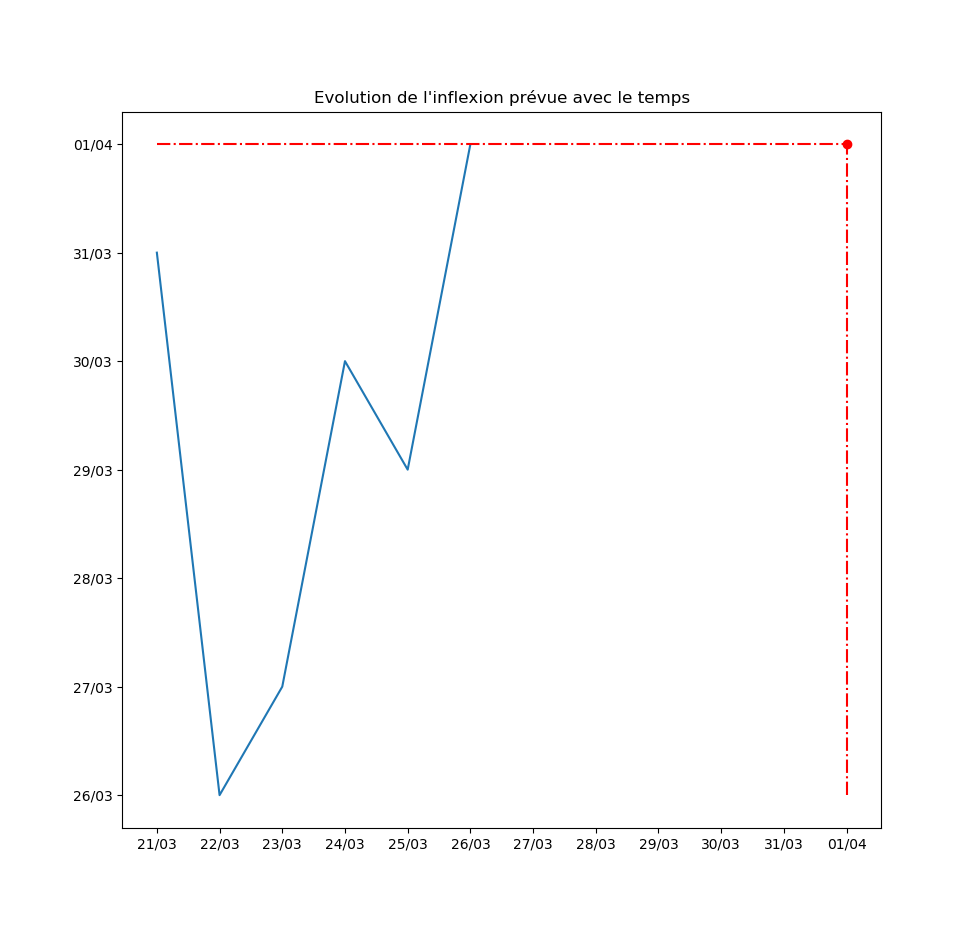
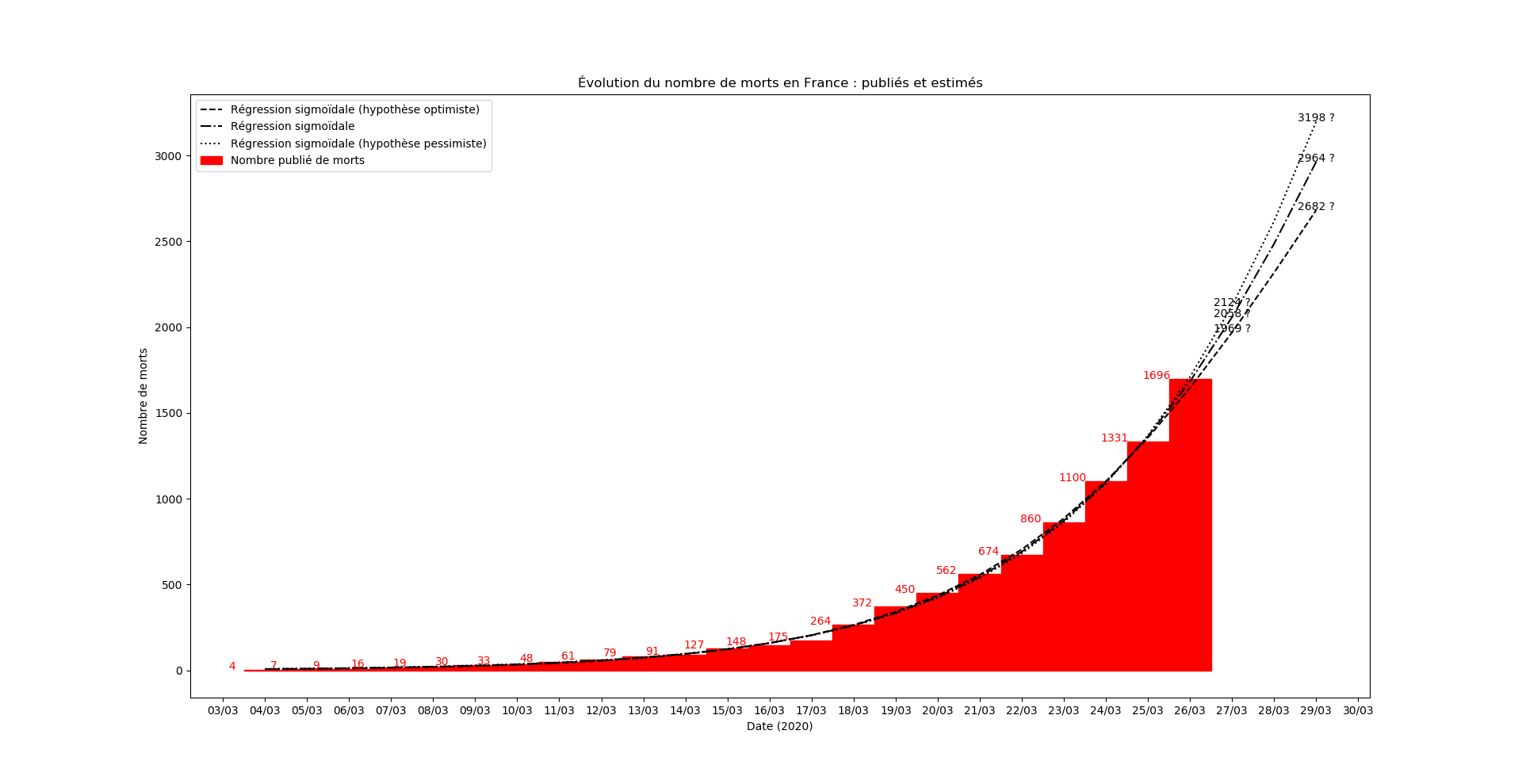
Mise-à-jour du 27 mars au soir