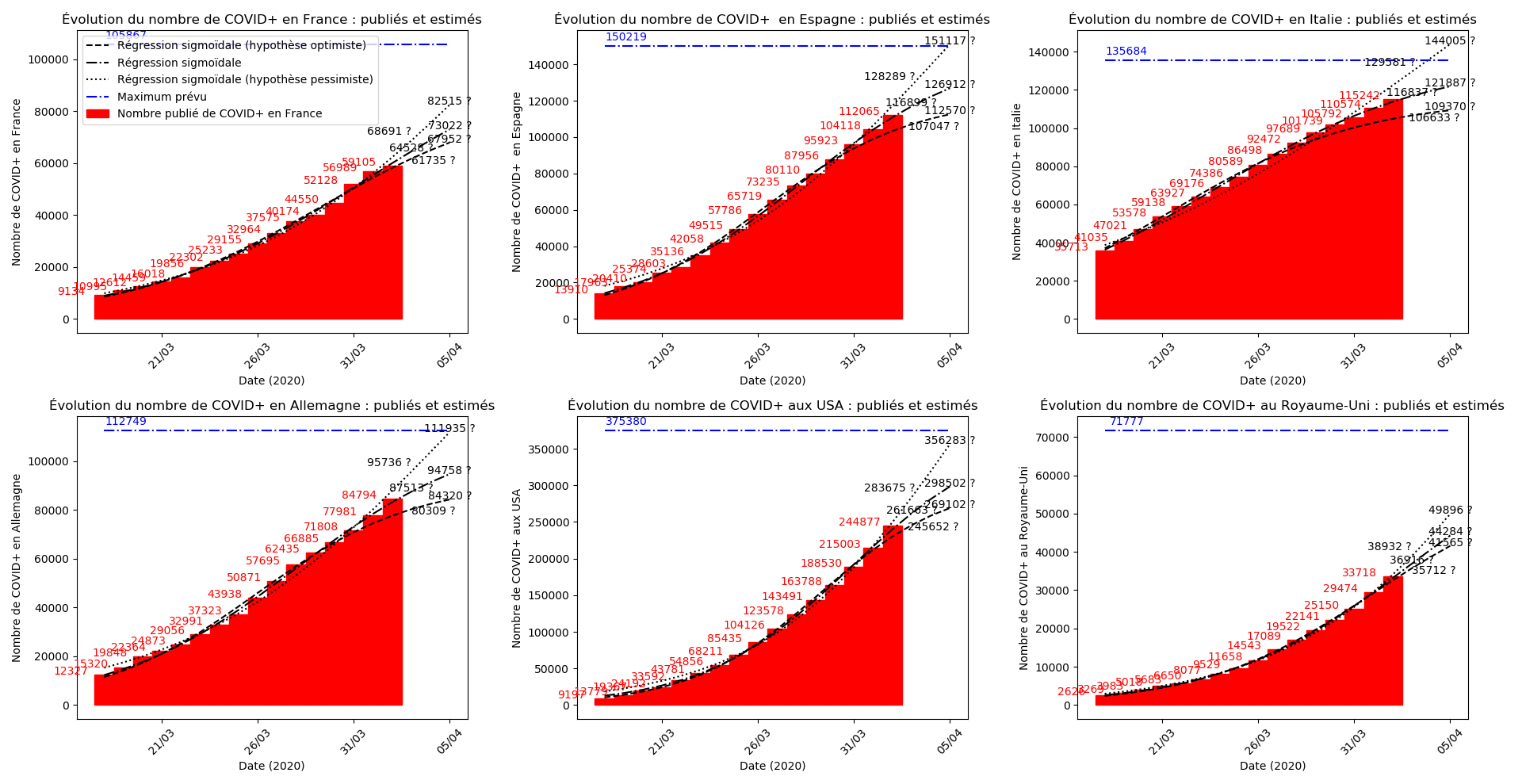
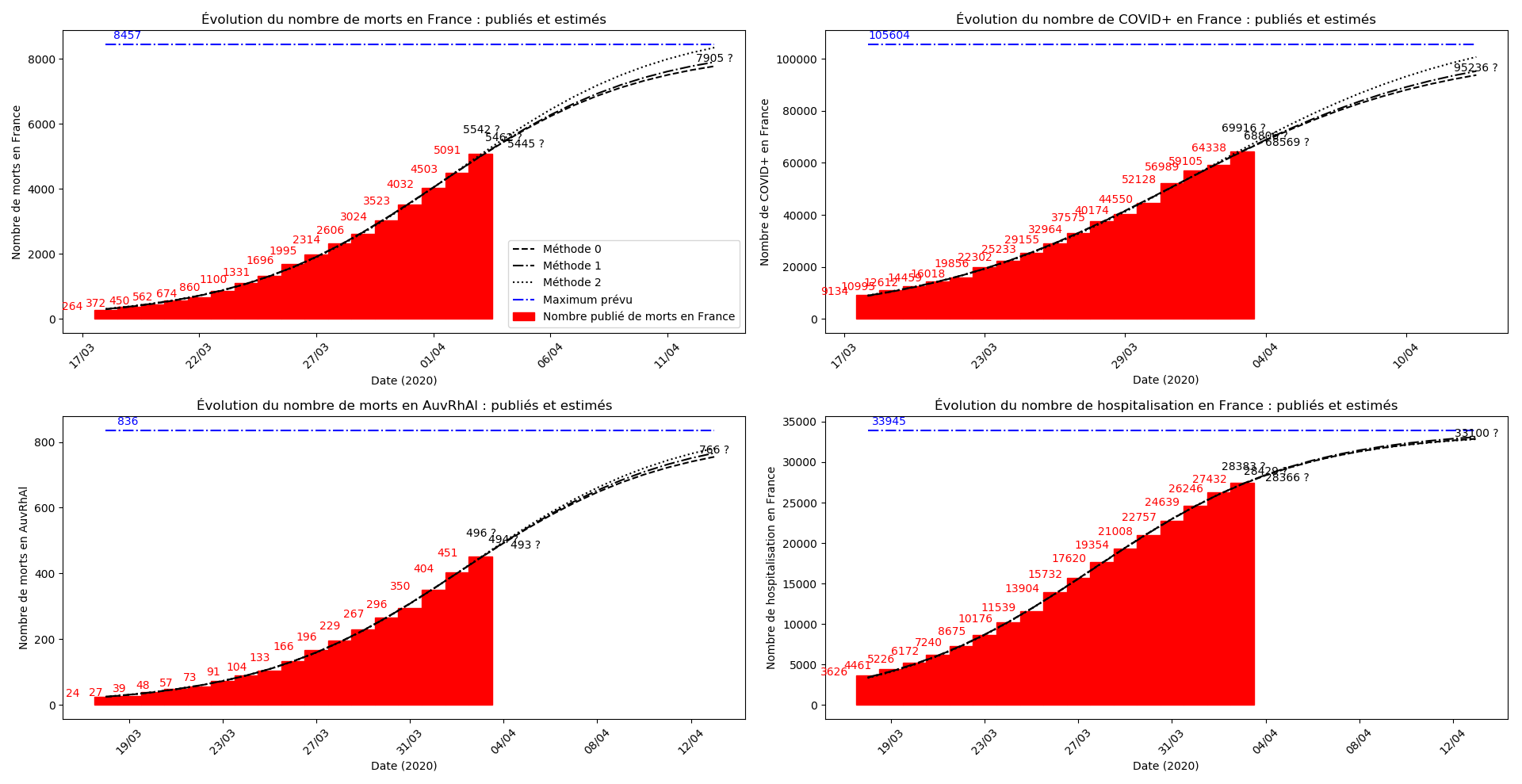
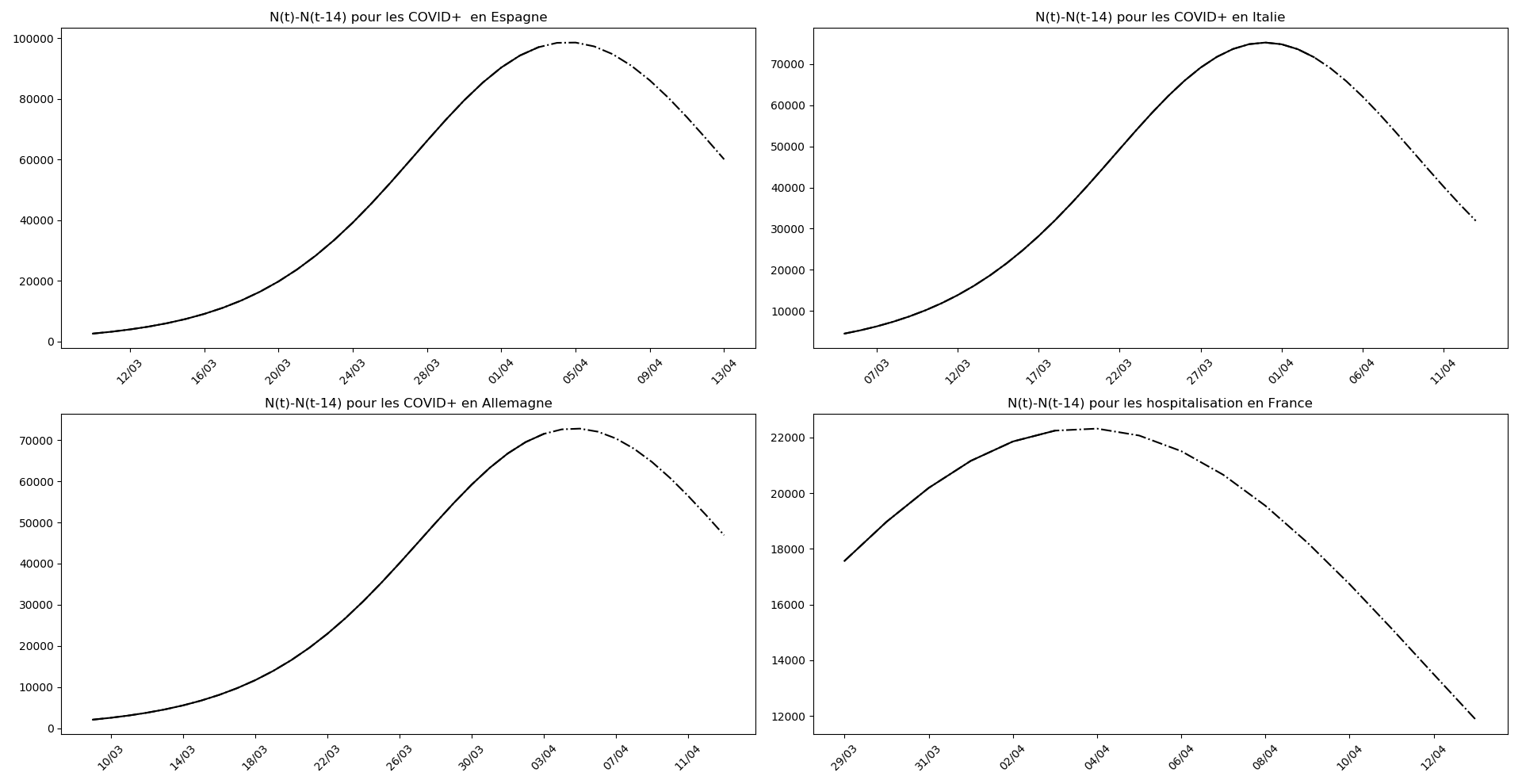
(Situation au 8 avril au soir)
Cet article fait suite à mon deuxième article où je présentais rapidement une méthode d’interpolation des données qui déferlent actuellement sur le nombre de malades du CoViD-19. Il est entaché d’une erreur de calcul.
J’explique dans un quatrième article pourquoi cette erreur s’avère… miraculeuse ! Elle me permet d’avoir trois méthodes différentes pour l’interpolation des données de l’épidémie, et non seulement m’évitent de créer artificiellement des simulations optimistes et pessimistes qui n’étaient pas fondées sur le plan théorique, mais aussi stabilisent la convergence de l’algorithme et empêchent l’apparition de jeux de paramètres aberrants.
Je rentre ici dans le détail de la méthode utilisée par le premier algorithme (fautif). Je fournis aussi un code Python permettant de comparer l’évolution de la maladie dans différents pays.
Position du problème
On souhaite approximer un nuage de points par une sigmoïde : nous noterons \(f(a,b,c):x\in\mathbb{R}\mapsto\dfrac{c}{1+e^{-(ax+b)}}=\dfrac{c}{1+e^{-a(x-t_0)}}\) les fonctions que nous souhaitons utiliser pour cette approximation.
Le nuage de points est donné par la liste $\left((X_i;Y_i)\right)_{1\leq i\leq n}$ de ses coordonnées.
Ici les abscisses $\left(X_i\right)_{1\leq i\leq n}$ sont les dates des mesures effectuées.
Et $\left(Y_i\right)_{1\leq i\leq n}$ sont les nombres de malades fournis par les gouvernements jour après jour.
On jugera de la qualité d’une approximation par la somme des carrés des écarts entre les données réelles $Y_i$ et leurs estimations $f(a,b,c)(X_i)$. Autrement dit, on utilise la méthode des moindres carrés qui consiste à minimiser la quantité \(S(a,b,c)=\displaystyle\sum_{i=1}^n\left[f(a,b,c)(X_i)-Y_i\right]^2\)
Remarquons avant d’entrer dans le détail que :
- $f$ étant continue relativement à l’ensemble de ses variables et $S$ étant positive, soit ce minimum existe et est atteint, soit la meilleure approximation correspond à des valeurs limites pour $(a;b;c)$. On exclut ici ce dernier cas.
- Éventuellement, plusieurs triplets $(a,b,c)$ réalisent ce minimum. Nous en cherchons un.
- $f$ étant aussi différentiable, un point $(a,b,c)$ réalisant ce minimum annule les trois dérivées partielles $\dfrac{\partial S}{\partial a}$, $\dfrac{\partial S}{\partial b}$ et $\dfrac{\partial S}{\partial c}$.
Nous noterons enfin dans tout ce qui suit $F_c:u\mapsto\dfrac{c}{1+e^{-u}}$ et $G_c:u\mapsto\ln\left(\dfrac{u}{c-u}\right)$ qui sont bijections réciproques l’une de l’autre. Autrement dit $F_c\left(G_c(u)\right)=u$ et $G_c\left(F_c(u)\right)=u$. La raison d’être de ces deux notations est que $G_c\left(f(a,b,c)(X_i)\right)=aX_i+b$, ce qui, nous le verrons, nous permettra de ramener le problème de départ à un problème bien connu qui est celui de la régression linéaire.
Recherche d’un point annulant les dérivées partielles
Commençons par calculer les dérivées partielles données plus haut :
\[\dfrac{\partial S}{\partial a}=2\displaystyle\sum_i\left(f(a,b,c)(X_i)-Y_i\right)\times\dfrac{cX_i\exp\left(-(aX_i+b)\right)}{\left(1+\exp\left(-(aX_i+b)\right)\right)^2}\] \[\dfrac{\partial S}{\partial b}=2\displaystyle\sum_i\left(f(a,b,c)(X_i)-Y_i\right)\times\dfrac{c\exp\left(-(aX_i+b)\right)}{\left(1+\exp\left(-(aX_i+b)\right)\right)^2}\] \[\dfrac{\partial S}{\partial c}=2\displaystyle\sum_i\left(f(a,b,c)(X_i)-Y_i\right)\times\dfrac{1}{1+\exp\left(-(aX_i+b)\right)}\]Comme ces trois dérivées doivent être nulles, on peut en déduire trois expressions donnant $c$ en fonction de $(a,b)$ lorsque ceux-ci sont connus. Par exemple, de la nullité de la troisième dérivée partielle en un point $(a,b,c)$ minimisant $S$, on tire que - pour ce point réalisant le minimum -:
\[(E_1):~~c=\dfrac{\displaystyle\sum_i\frac{Y_i}{1+\exp\left(-(aX_i+b)\right)}}{\displaystyle\sum_i\frac{1}{\left(1+\exp\left(-(aX_i+b)\right)\right)^2}}\]La manipulation de ces trois équations - $(E_1)$ et celles qu’on obtient en annulant aussi les dérivées partielles par rapport aux deux autres variables - est cependant trop difficile pour conduire à une solution du problème.
Pour parvenir à nos fins, notons $L_i=G_c(Y_i)$ et réécrivons $S$ sous une autre forme : \(S(a,b,c)=\displaystyle\sum_{i=1}^n\left[f(a,b,c)(X_i)-Y_i\right]^2=\sum_{i=1}^n\left[F_c(aX_i+b)-F_c(L_i)\right]^2\)
En utilisant le développement limité de $F_c$ au voisinage de $L_i$ on obtient une expression approximative de $S$ : \(S(a,b,c)\approx\displaystyle\sum_{i=1}^n\left[F_c'(L_i)\left(aX_i+b-L_i\right)\right]^2\)
\[S(a,b,c)\approx\sum_i\left(aX_i+b-L_i\right)^2aY_i^2\left(1-\frac{Y_i}{c}\right)^2\]À nouveau, on peut écrire les dérivées partielles de $S$ par rapport à $a$ et $b$ et affirmer qu’elles s’annulent en un point réalisant le minimum. Les calculs conduisent alors aux expressions suivantes : on note
- $P_i=L_i^2\left(1-\frac{L_i}{c}\right)^2$
- $\overline{L}=\dfrac{\displaystyle\sum_iP_iL_i}{\displaystyle\sum_iP_i}$
- $\overline{X}=\dfrac{\displaystyle\sum_iP_iX_i}{\displaystyle\sum_iP_i}$
- $\overline{A}=\displaystyle\sum_iP_i\left(X_i-\overline{X}\right)\left(2X_i-\overline{X}\right)$
- $\overline{B}=\displaystyle\sum_iP_i\left(3X_i-2\overline{X}\right)\left(\overline{L}-L_i\right)$
- $\overline{C}=\displaystyle\sum_iP_i\left(\overline{L}-L_i\right)^2$
- $\overline{\Delta}=\overline{B}^2-4\overline{A}\overline{C}$
Résumé et algorithme
Les équations $(E_1)$ d’une part, et $(E_2)$ et $(E_3)$ d’autre part, permettent pour la première de calculer $c$ connaissant $(a;b)$ et pour les deux suivantes de calculer $a$ et $b$ connaissant $c$.
De plus, pour que $L_i=G_c(Y_i)$ soit défini, il faut que $c>\max\left(Y_i\right)_{1\leq i\leq n}$.
Le principe de l’algorithme est alors le suivant :
- on pose $c_0=2\times\max\left(Y_i\right)_{1\leq i\leq n}$;
- connaissant $c_0$, on calcule $a_0$ et $b_0$ en utilisant $(E_2)$ et $(E_3)$;
- grâce aux valeurs de $a_0$ et $b_0$, on calcule $c_1$ en utilisant $(E_1)$;
- on continue ainsi jusqu’à ce que $c_{j+1}-c_j$ soit inférieur, en valeur absolue, à une précision voulue;
- les valeurs $\left(a_{j+1};b_{j+1};c_{j+1}\right)$ sont alors les valeurs souhaitées.
Algorithme
"""
Created on Fri Mar 6 16:04:15 2020
@author: François Coulombeau
"""
import numpy as np
import matplotlib.pyplot as plt
import datetime as dtm
import matplotlib.dates as mdates
import matplotlib.patches as mpat
import os
Param_a = 0
Param_b = 1
Param_c = 2
Taux = 3
Inflexion = 4
Prev_vs_Real = 5
Fit = 6
Pic = 7
e = 2
def reglin(X,Y,poids):
"""Calcul des coefficients de la droite de régression Y = a*X+b où chaque
point (x_i,y_i) est pondéré par le poids donné dans la liste optionnelle."""
poids = np.array(poids)
N = np.sum(poids)
poids = poids/N
moyX = sum(poids*X)
moyY = sum(poids*Y)
A = sum(poids*(X-moyX)*(2*X-moyX))
B = sum(poids*(3*X-2*moyX)*(moyY-Y))
C = sum(poids*(Y-moyY)**2)
Delta = B**2-4*A*C
a = (-B+Delta**0.5)/A/2
b = moyY-a*moyX
# print("Corrélation : ",(sum(poids*(Y-a*X-b)**2)/sum(poids*Y**2))**0.5)
return a,b
def f(a,b,c):
"""Renvoie la fonction sigmoïde correspondante."""
return lambda x:c/(1+np.exp(-(a*x+b)))
def interpSigm2(data, fin, Inf=None, Sup=None,
S0=0, mxS=1e6, err=1.5, nbInt=500):
"""Calcule les paramètres (a,b,c) de la sigmoïde ainsi que les versions
optimiste : (am,bm,cm)
pessimiste : (aM,bM,cM)"""
n = len(data)
somcum = [S0+sum(data[:(k+1)]) for k in range(n)]
somcum = np.array(somcum[:fin])
if Inf is None:
Inf = np.max(somcum)+2
if Sup is None:
Sup = mxS
mn=np.infty
X = np.array(range(fin))
tab = []
for c in np.exp(np.linspace(np.log(Inf),np.log(Sup),nbInt)):
Y0 = np.log(somcum/(c-somcum))
a,b = reglin(X,Y0,(somcum*(1-somcum/c)))
fX = f(a,b,c)(X)
S = sum((somcum-fX)**2)
tab.append((a,b,c,S))
if S<=mn:
am,bm,cm = a,b,c
mn = S
a,b,c = am,bm,cm
tab = [k for k in tab if k[3]<err*mn]
am,bm,cm = tab[0][:3]
aM,bM,cM = tab[-1][:3]
return ((am,bm,cm),(a,b,c),(aM,bM,cM))
def interpSigm(data, fin, S0=0, mxS=1e6, err=1.5, prec=1e-3,method = 1):
"""Calcule les paramètres (a,b,c) de la sigmoïde ainsi que les versions
optimiste : (am,bm,cm)
pessimiste : (aM,bM,cM)"""
n = len(data)
somcum = [S0+sum(data[:(k+1)]) for k in range(n)]
somcum = np.array(somcum[:fin])
X = np.array(range(fin))
c = max(somcum)*2
cn = 2*c
i=0
while (abs(c-cn)>prec*c and c<mxS) or (i<=2):
i+=1
Y0 = np.log(somcum/(c-somcum))
a,b = reglin(X,Y0,(somcum*(1-somcum/c))**e)
cn = c
c = np.sum(somcum*f(a,b,1)(X))/np.sum(f(a,b,1)(X)**e)
if c>mxS or np.isnan(c):
c=mxS
Y0 = np.log(somcum/(c-somcum))
a,b = reglin(X,Y0,(somcum*(1-somcum/c))**e)
else:
Y0 = np.log(somcum/(c-somcum))
a,b = reglin(X,Y0,(somcum*(1-somcum/c))**e)
if method:
cm = max(c/err**0.3,max(somcum)+1)
Y0 = np.log(somcum/(cm-somcum))
am,bm = reglin(X,Y0,(somcum*(1-somcum/cm))**e)
cM = c*err
Y0 = np.log(somcum/(cM-somcum))
aM,bM = reglin(X,Y0,(somcum*(1-somcum/cM))**e)
return ((am,bm,cm),(a,b,c),(aM,bM,cM))
else:
m,L,M = interpSigm2(data,fin,
Inf=max(np.max(somcum)+1,c/err), Sup=c*err,
S0=S0,mxS=mxS,err=err,nbInt=500)
return m,L,M
def caracteristiques(a,b,c,d):
"""Calcule trois paramètres caractéristiques
- taux de croissance instantané
- taux de croissance en -infini
- jour d'inflexion
à partir des valeurs de (a,b,c)
et de celle du jour d pour lequel on cherche la croissance instantanée."""
taux = a*np.exp(-(a*d+b))/(1+np.exp(-(a*d+b)))
tauxInit = np.exp(a)-1
inflexion = -b/a
return taux,tauxInit,inflexion
def plt_set_fullscreen():
backend = str(plt.get_backend())
mgr = plt.get_current_fig_manager()
if backend == 'TkAgg':
if os.name == 'nt':
mgr.window.state('zoomed')
else:
mgr.resize(*mgr.window.maxsize())
elif backend == 'wxAgg':
mgr.frame.Maximize(True)
elif backend[:2] == 'Qt':
mgr.window.showMaximized()
def figDate(both=False,logscale=False, sbp = None, intervalle=1):
# Nouvelle figure et paramétrage
if sbp == None:
plt.figure()
else:
plt.subplot(sbp)
ax = plt.gca()
formatter = mdates.DateFormatter("%d/%m")
ax.xaxis.set_major_formatter(formatter)
locator = mdates.DayLocator(interval=intervalle)
ax.xaxis.set_major_locator(locator)
if both:
ax.yaxis.set_major_formatter(formatter)
locator = mdates.DayLocator()
ax.yaxis.set_major_locator(locator)
if logscale:
ax.yscale='log'
def evol(dates,listes,titre,typeDonnees, sbp = None, legend=True):
Lam,La,LaM = listes
inter = len(dates)//10+1
figDate(sbp=sbp,intervalle=inter)
plt.plot(dates,La,'k')
plt.plot(dates,Lam,'-.k')
plt.plot(dates,LaM,':k')
plt.title(titre+"""
pour les """+typeDonnees)
plt.xticks(rotation = 45)
if legend:
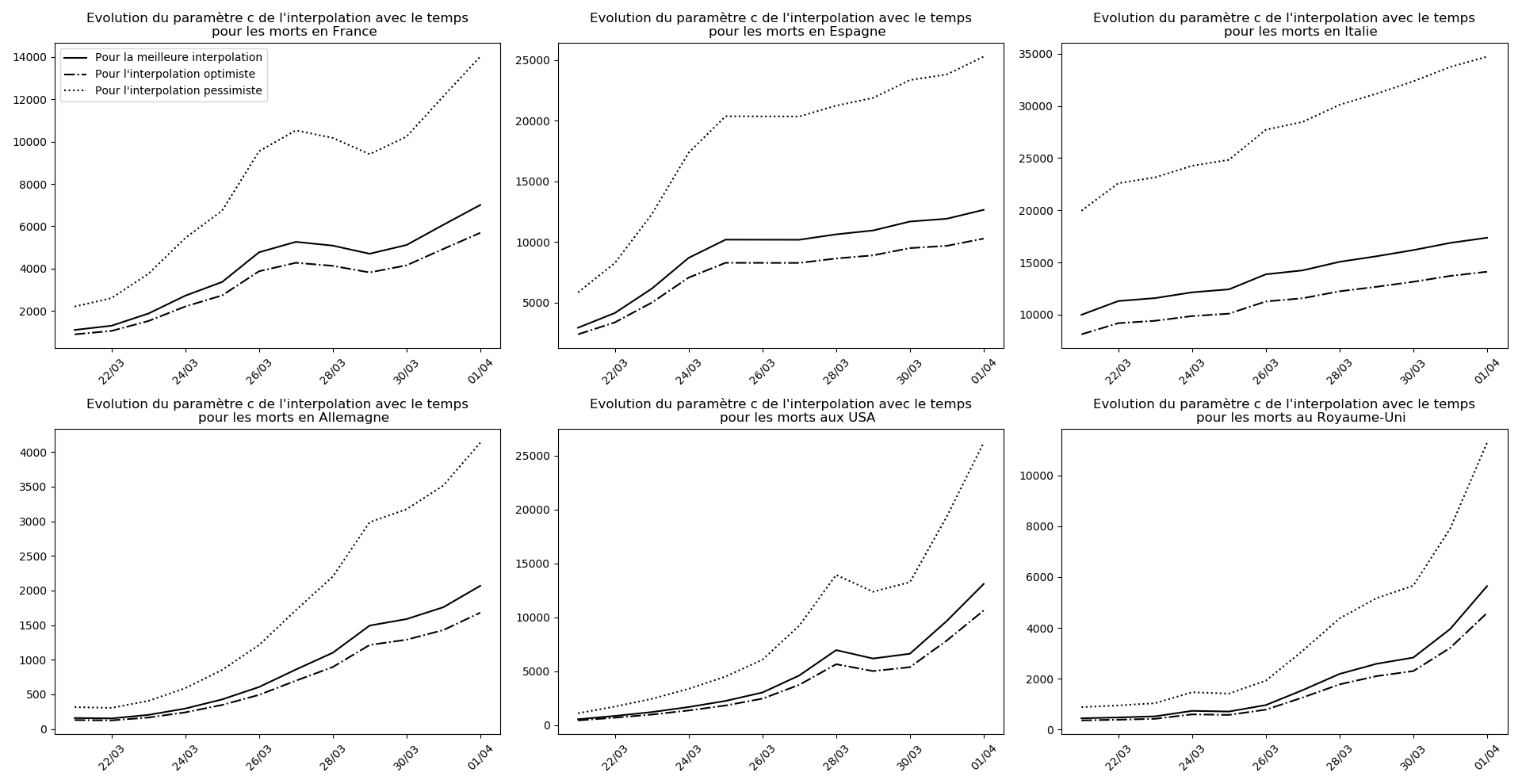
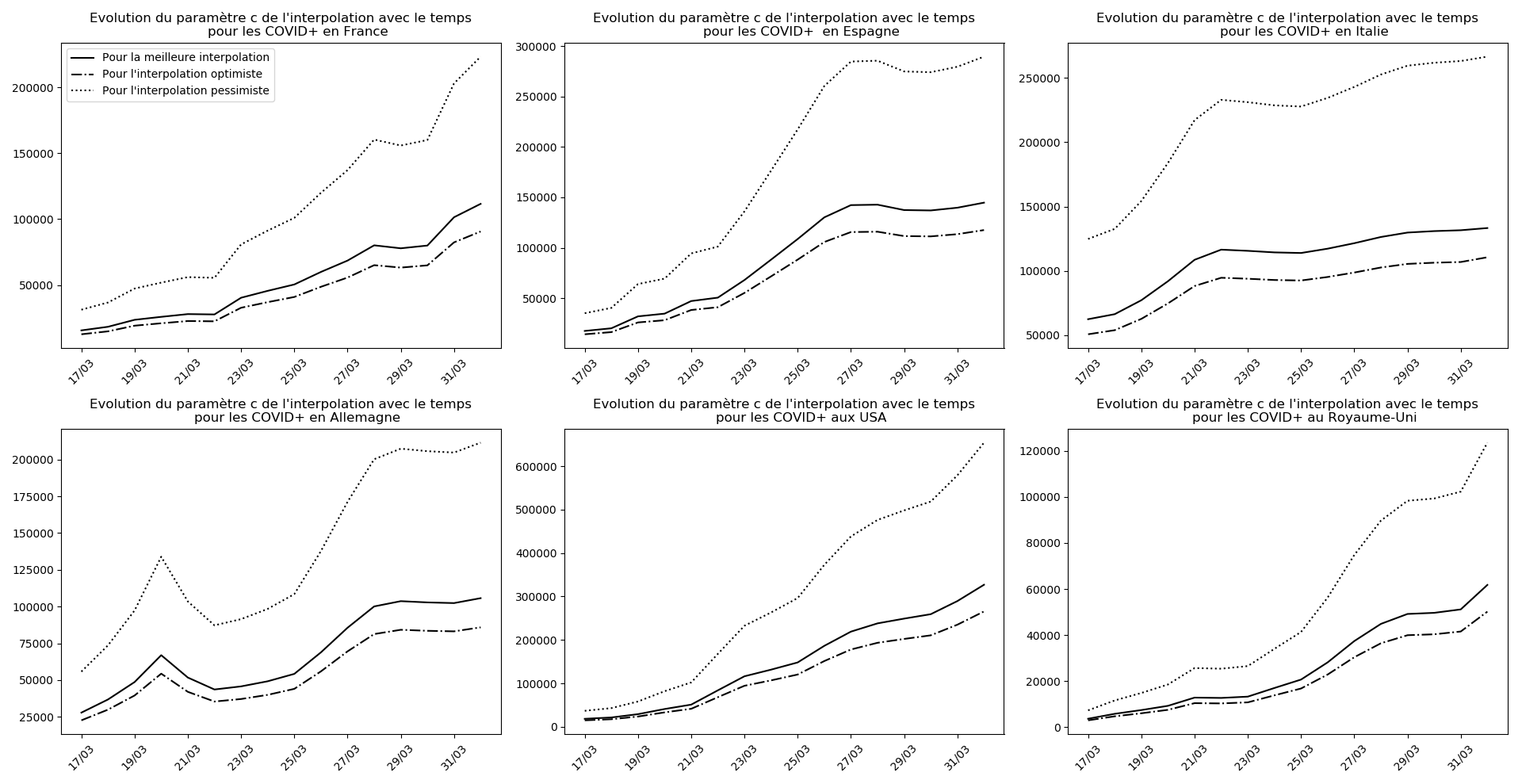
plt.legend(["Pour la meilleure interpolation",
"Pour l'interpolation optimiste",
"Pour l'interpolation pessimiste"])
def evol_taux(dates, T1, T2, typeDonnees, sbp = None, legend=True):
inter = len(dates)//10+1
figDate(sbp=sbp,intervalle=inter)
plt.plot(dates,T1)
plt.plot(dates,T2)
plt.title("""Evolution des taux caractéristiques et instantanés avec le temps
pour les """+typeDonnees)
plt.xticks(rotation = 45)
if legend:
plt.legend(["Taux d'évolution instantané",
"Taux d'évolution initial"])
def evol_inflexion(dates, T3, typeDonnees, sbp = None):
inter = len(dates)//10+1
figDate(both=True,sbp=sbp,intervalle=inter)
plt.plot(dates,T3)
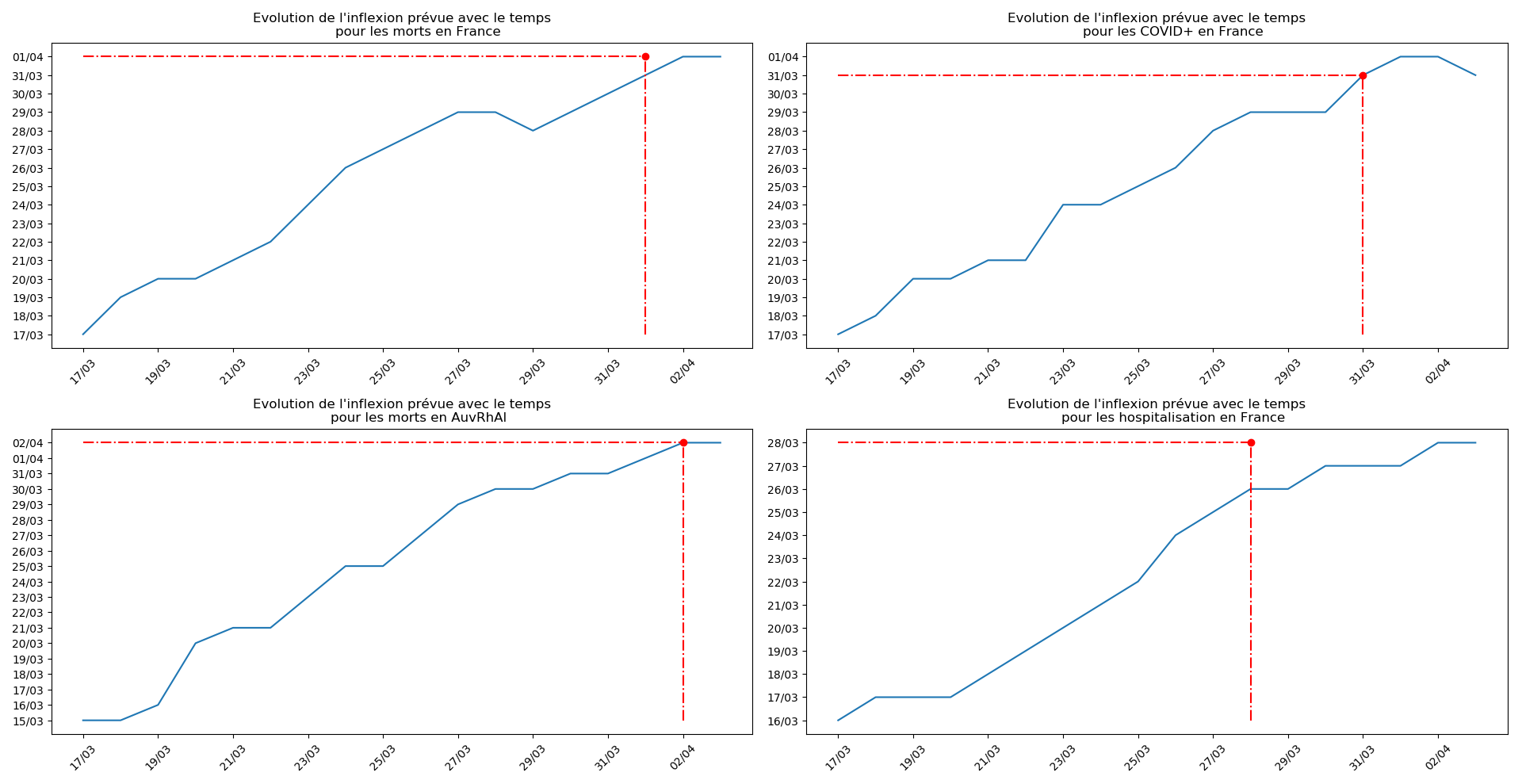
plt.title("""Evolution de l'inflexion prévue avec le temps
pour les """+typeDonnees)
plt.plot(T3[-1],T3[-1],'or')
plt.plot([dates[0],T3[-1]],[T3[-1],T3[-1]],'-.r')
plt.plot([T3[-1],T3[-1]],[np.min(T3),T3[-1]],'-.r')
plt.xticks(rotation = 45)
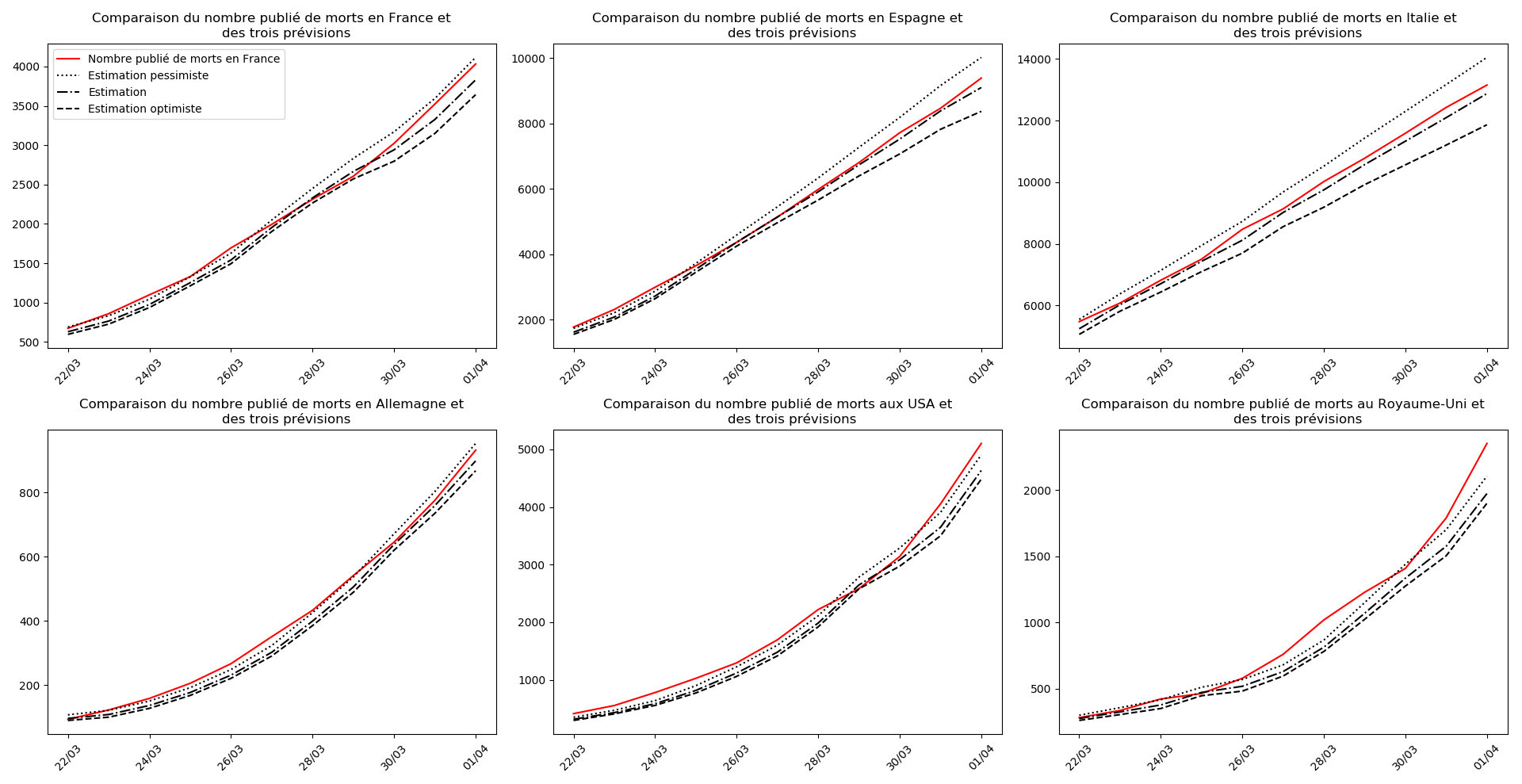
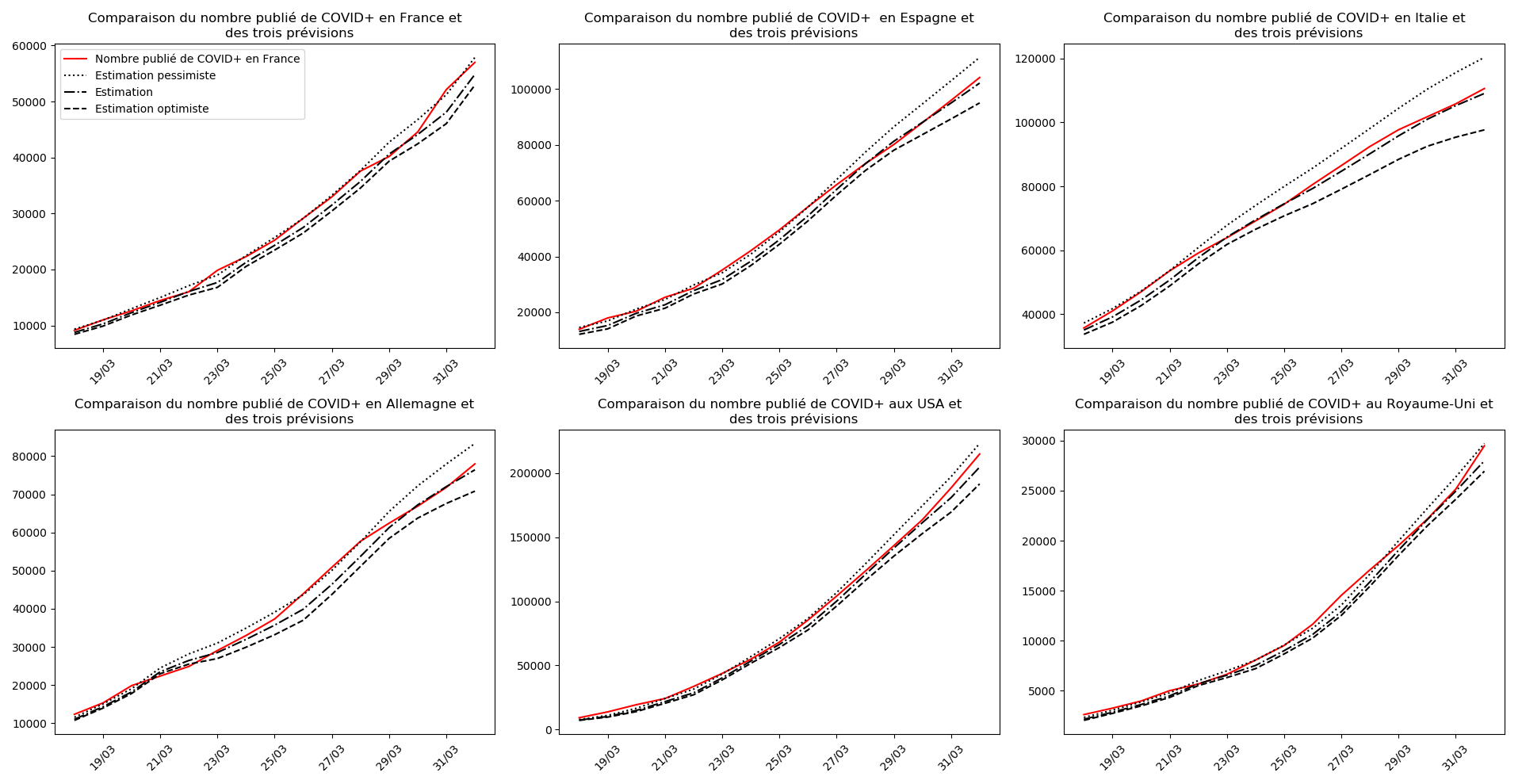
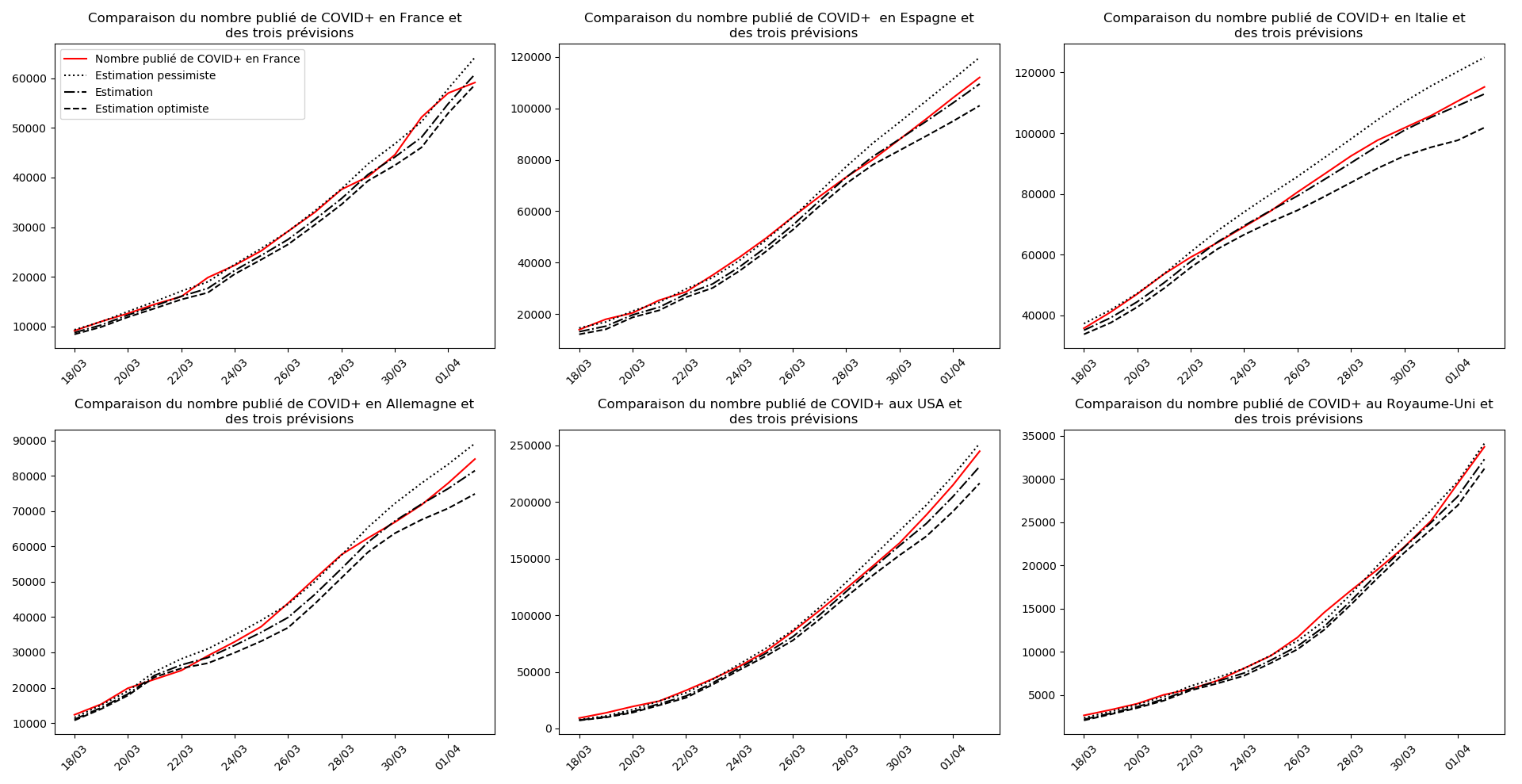
def evol_previsions(dates, listes, nouveaux, somcum, debf, typeDonnees,
sbp = None, legend=True):
n=len(nouveaux)
Lam,La,LaM,Lbm,Lb,LbM,Lcm,Lc,LcM = listes
inter = (n-debf)//10+1
figDate(sbp=sbp,intervalle=inter)
prev = [f(LaM[i],LbM[i],LcM[i])(debf+i) for i in range(n-debf)]
plt.plot(dates[1:],somcum[-n+debf:],'r')
plt.plot(dates[1:],prev,':k')
prev = [f(La[i],Lb[i],Lc[i])(debf+i) for i in range(n-debf)]
plt.plot(dates[1:],prev,'-.k')
prev = [f(Lam[i],Lbm[i],Lcm[i])(debf+i) for i in range(n-debf)]
plt.plot(dates[1:],prev,'--k')
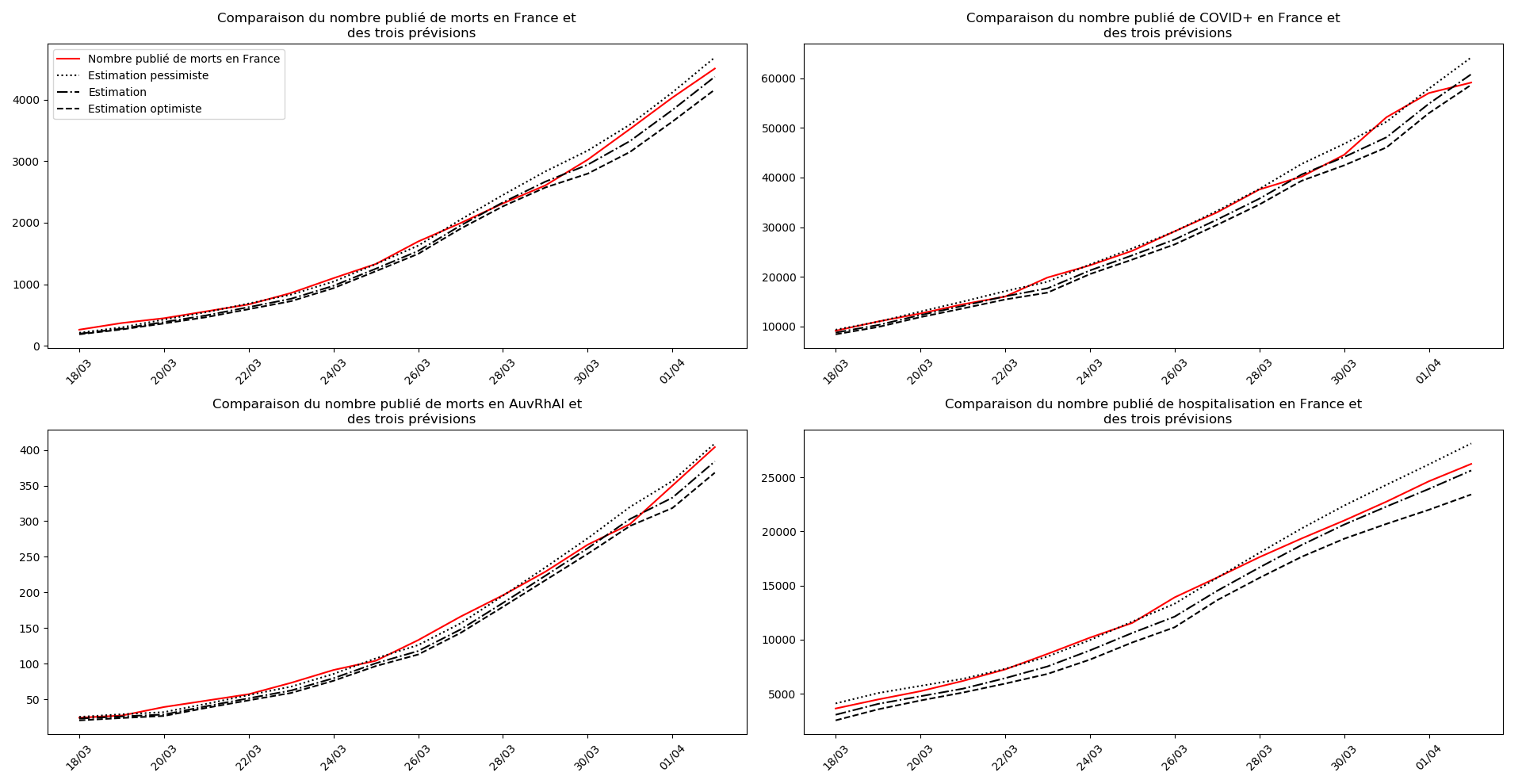
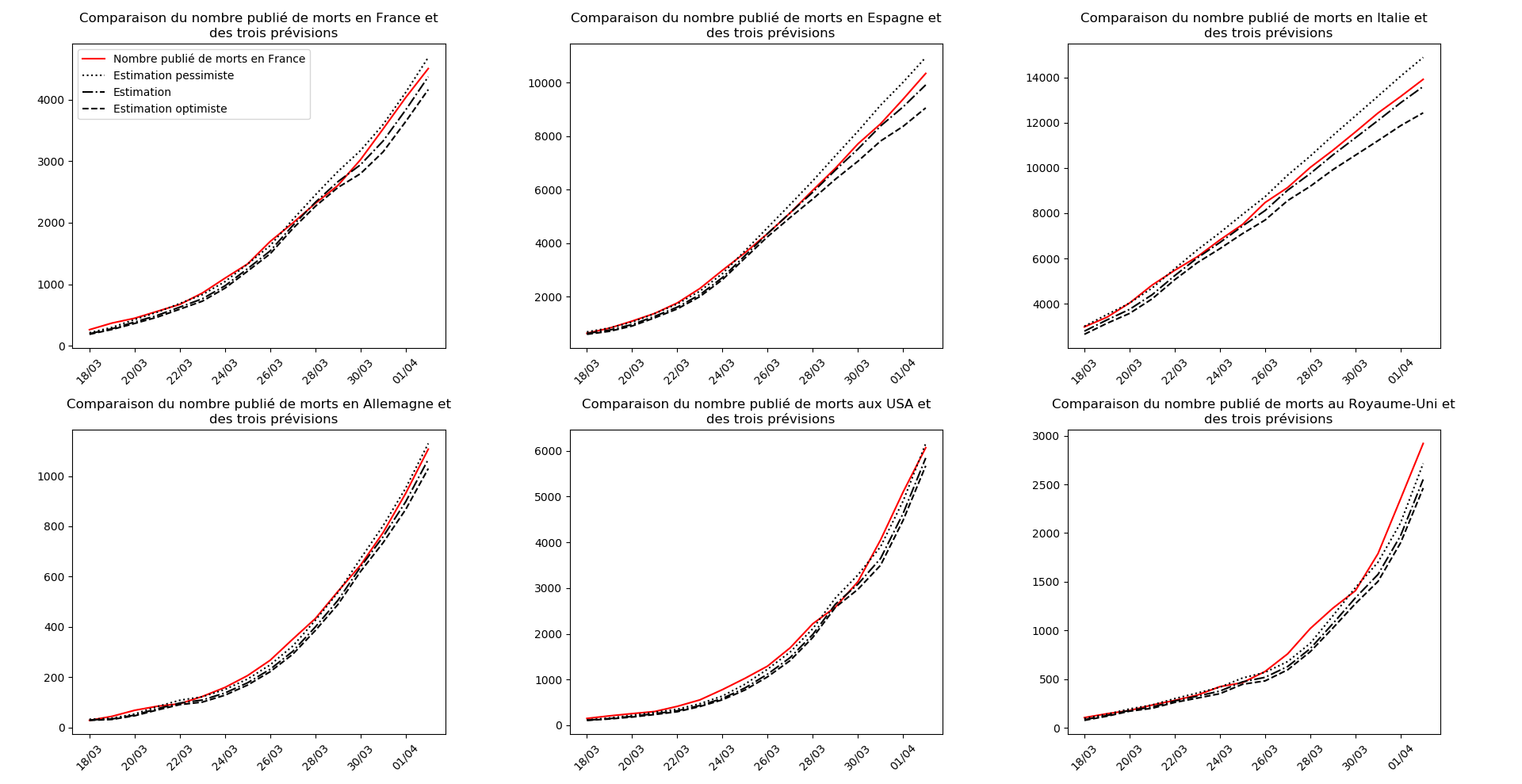
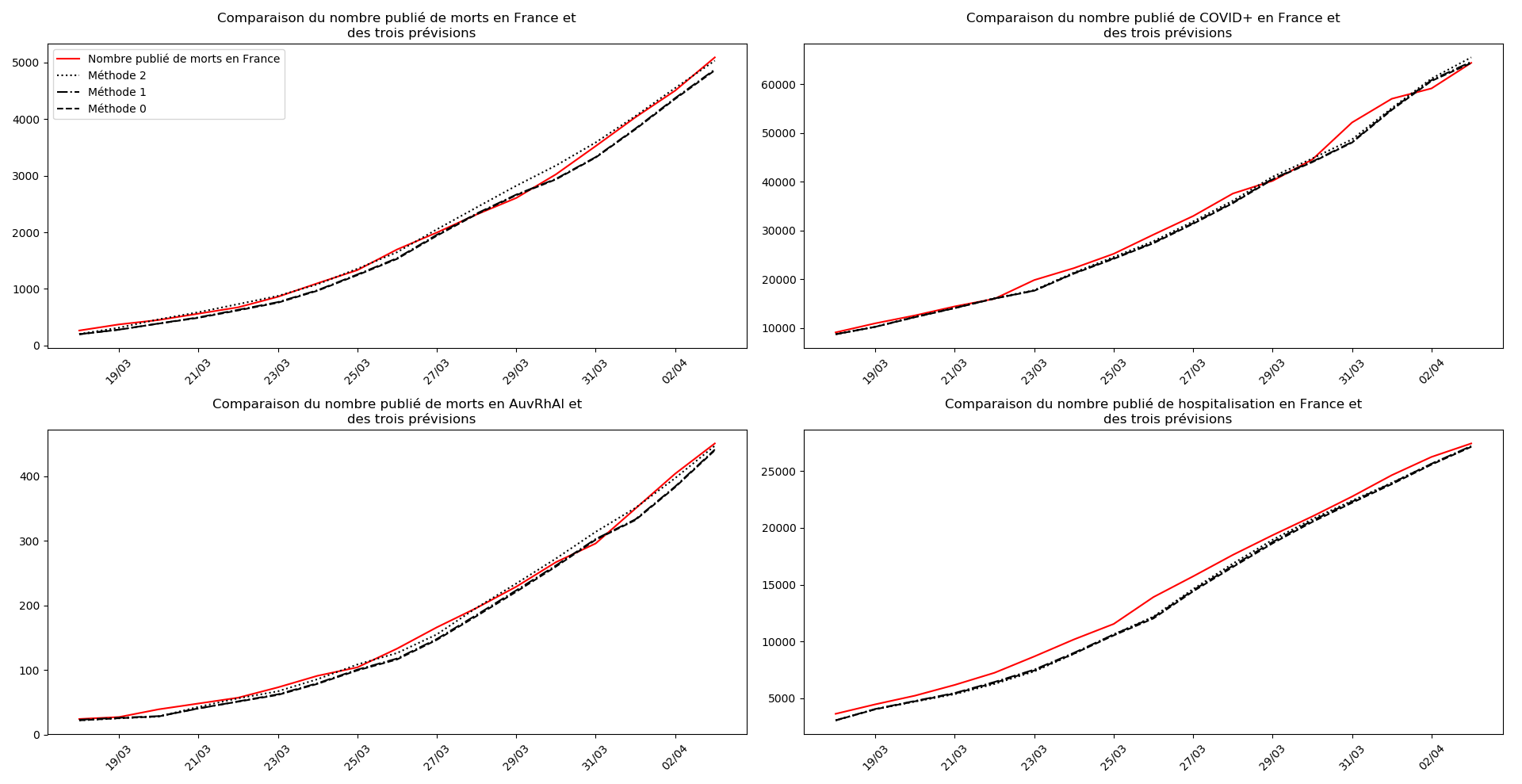
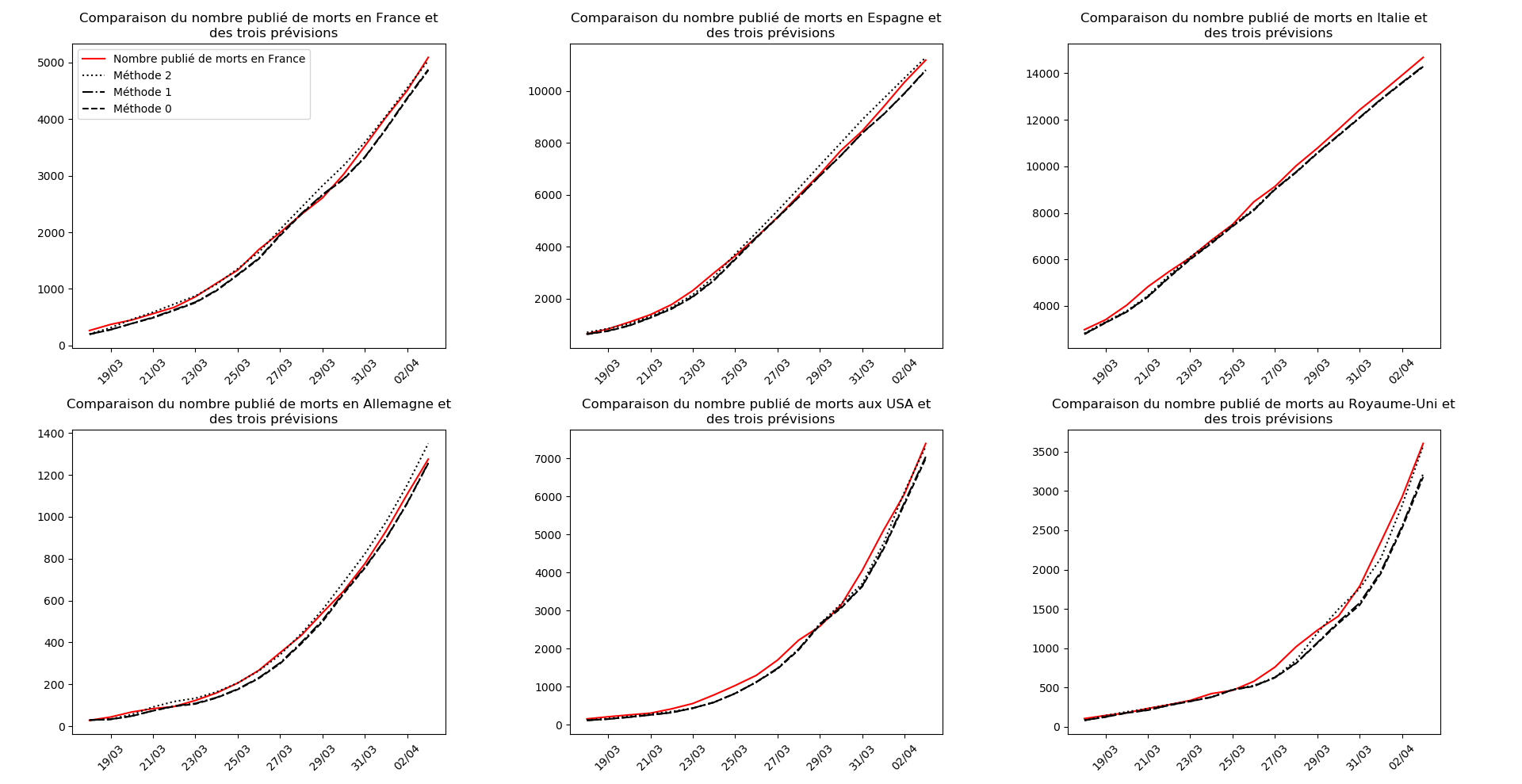
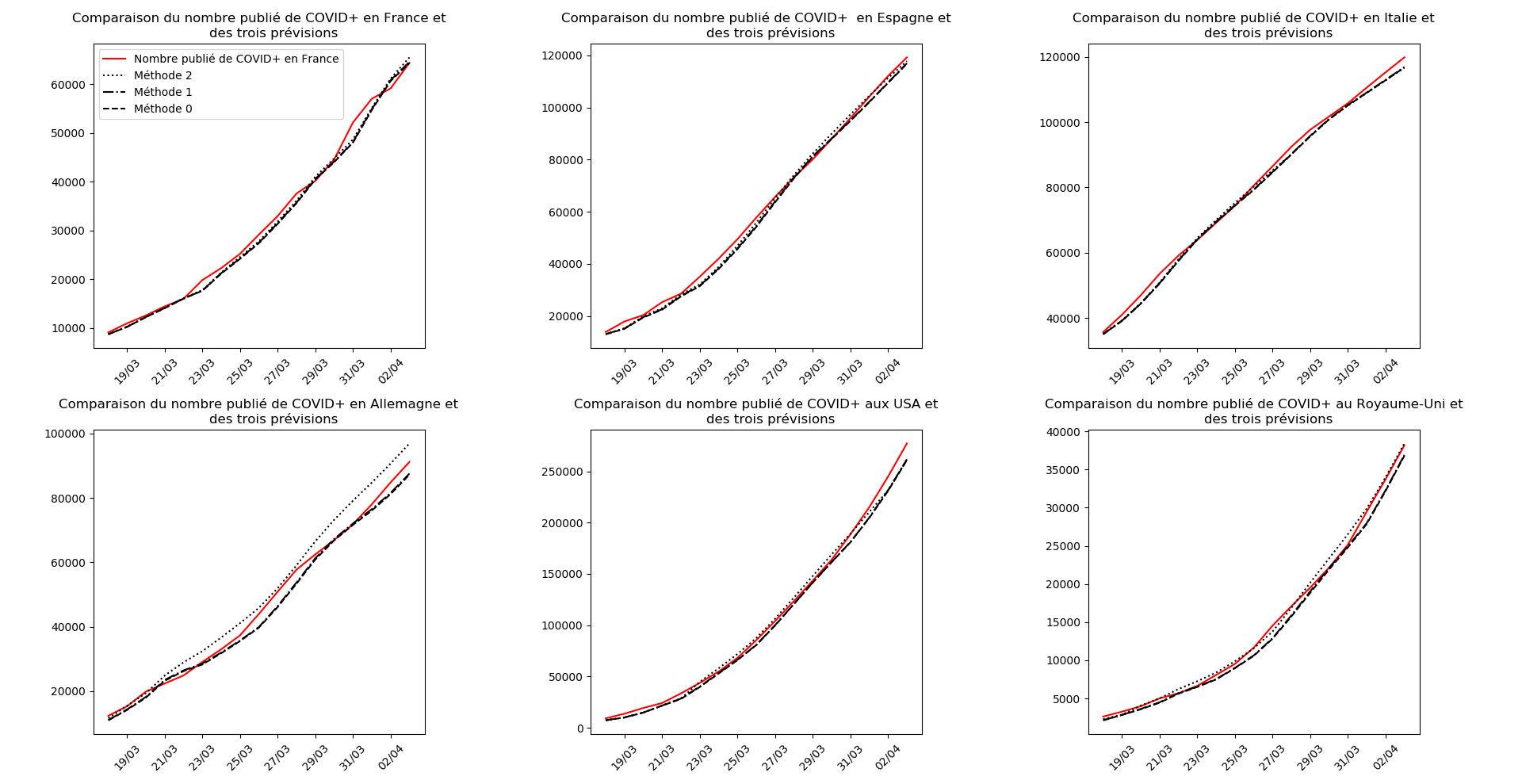
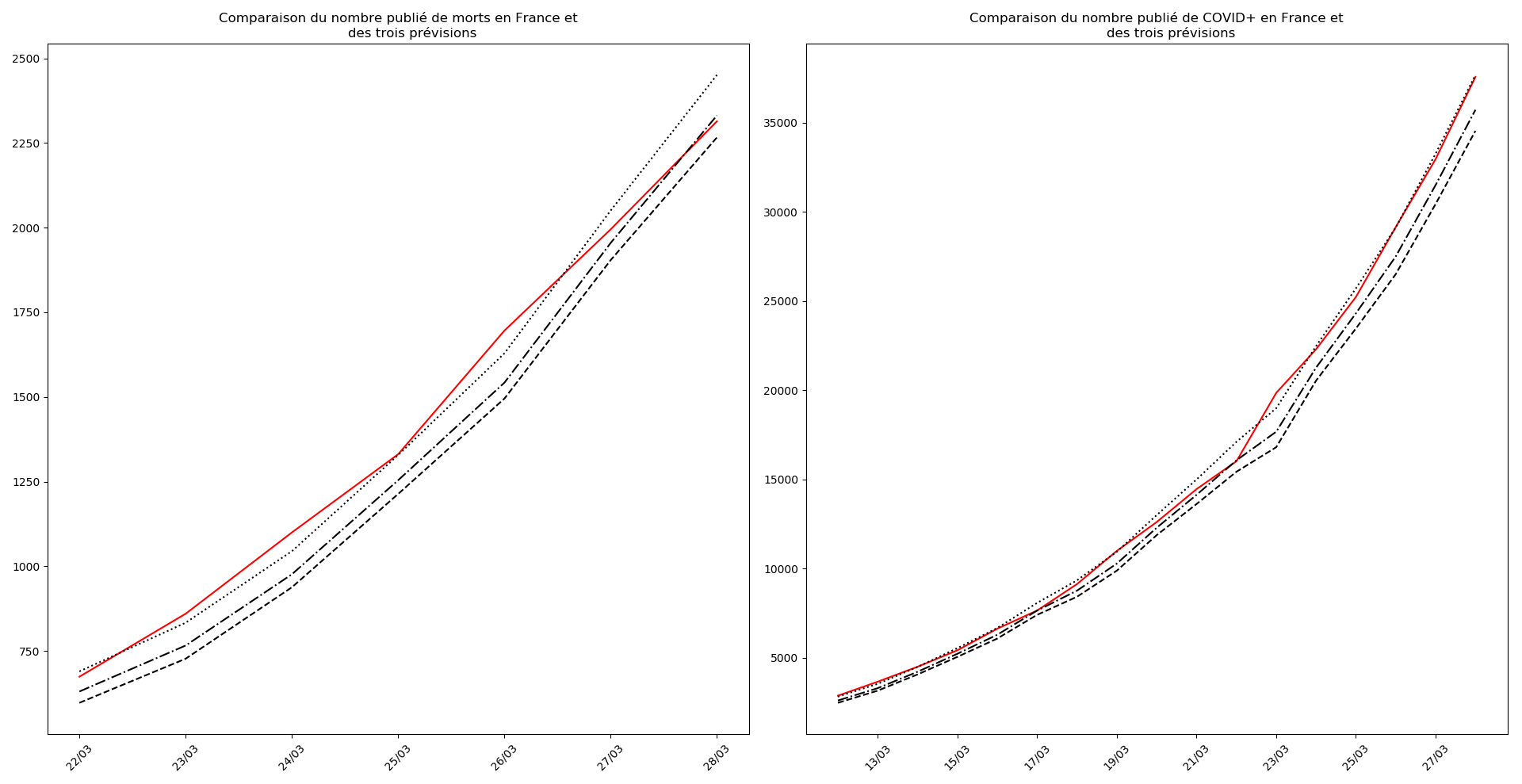
plt.title("""Comparaison du nombre publié de """+typeDonnees+""" et
des trois prévisions """)
plt.xticks(rotation = 45)
if legend:
plt.legend(["Nombre publié de "+typeDonnees,"Estimation pessimiste","Estimation",
"Estimation optimiste"])
def evol_pic(debd, dt, n, a, b, c, typeDonnees, sbp = None):
Delta = 14
inter = (n+dt-Delta)//10+1
figDate(sbp=sbp,intervalle = inter)
dates = [dtm.datetime.fromordinal(737448+debd+k+Delta) for k in range(n+dt-Delta)]
dates = [str(k.day)+'/'+str(k.month)+'/'+str(k.year) for k in dates]
lbl = [dtm.datetime.strptime(d,"%d/%m/%Y").date().toordinal() for d in dates]
XX = np.array(range(Delta,n+dt))
YY = f(a,b,c)(XX)-f(a,b,c)(XX-Delta)
plt.plot(lbl,YY,'-.k')
XX = np.array(range(Delta,n))
YY = f(a,b,c)(XX)-f(a,b,c)(XX-Delta)
plt.plot(lbl[:-dt],YY,'k')
plt.xticks(rotation = 45)
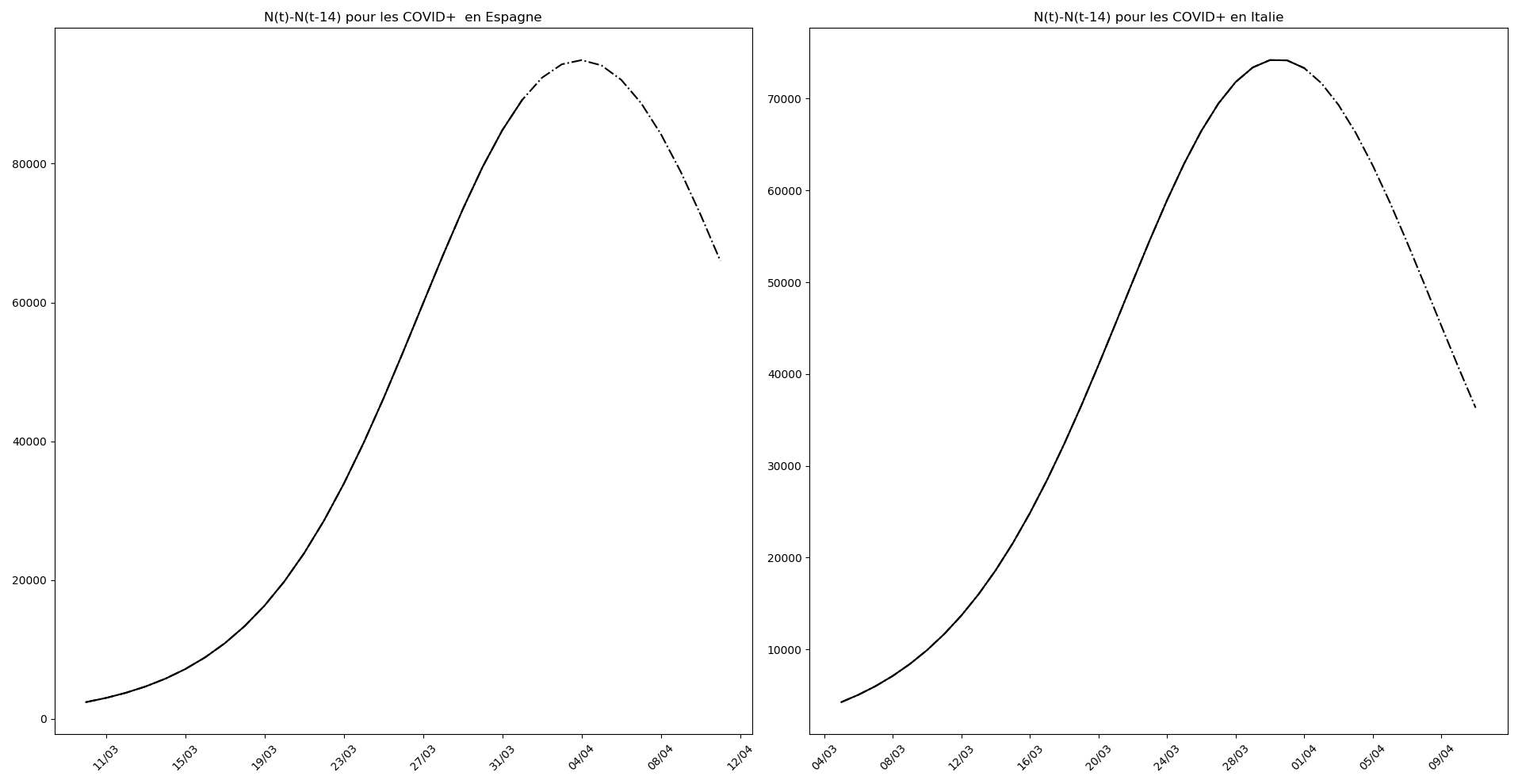
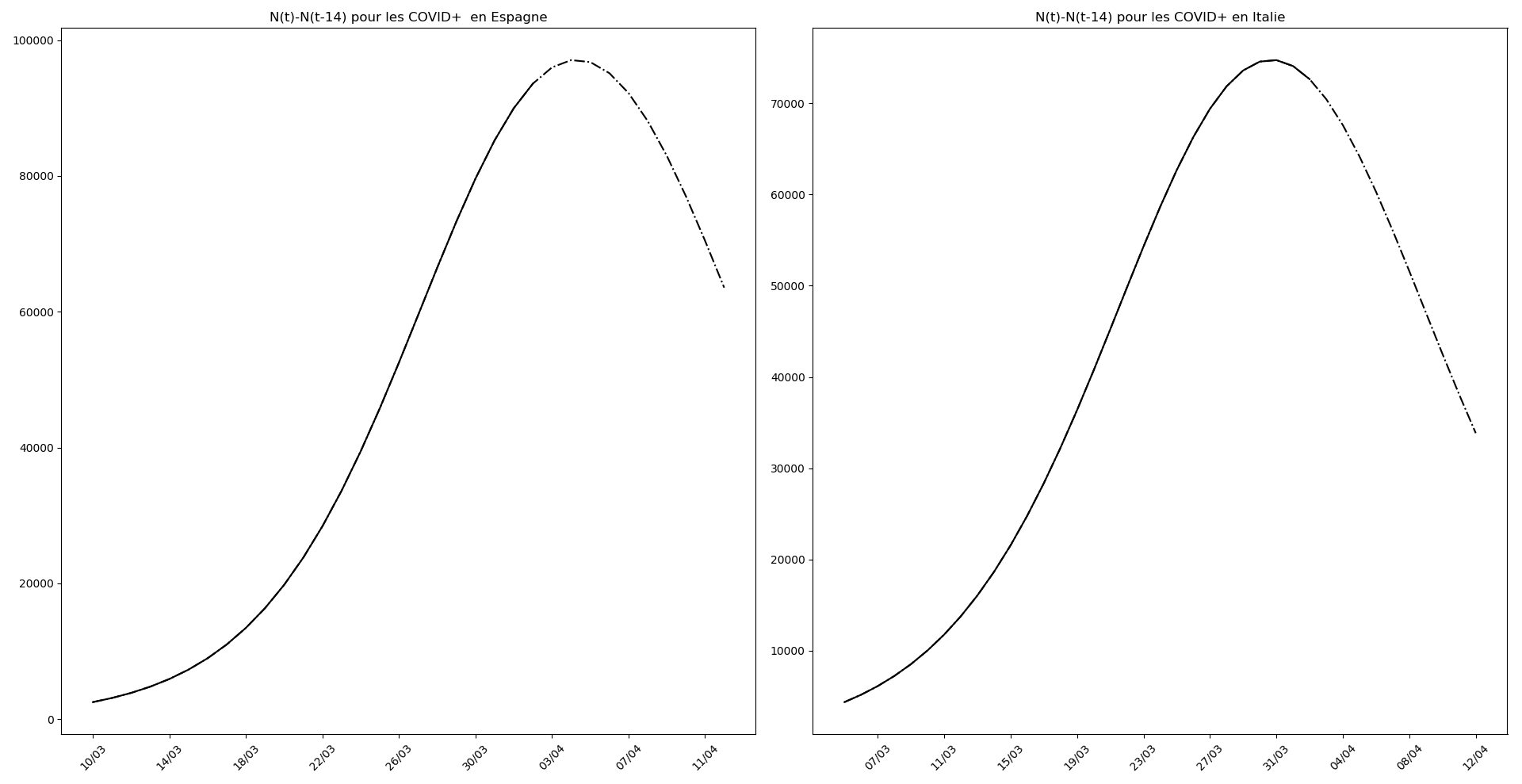
plt.title('N(t)-N(t-'+str(Delta)+') pour les '+typeDonnees )
def evol_cas(dates, liste, somcum, debd, debf, dt, typeDonnees, sbp = None,
legend=True):
am,a,aM,bm,b,bM,cm,c,cM = liste
n=len(somcum)
inter = (n+dt)//10+1
if sbp == None:
plt.figure()
ax = plt.gca()
formatter = mdates.DateFormatter("%d/%m")
ax.xaxis.set_major_formatter(formatter)
locator = mdates.DayLocator(interval = inter)
ax.xaxis.set_major_locator(locator)
else:
plt.subplot(sbp)
ax = plt.gca()
formatter = mdates.DateFormatter("%d/%m")
ax.xaxis.set_major_formatter(formatter)
locator = mdates.DayLocator(interval = inter)
ax.xaxis.set_major_locator(locator)
# Histogrammes du nombre publié de morts
dates = [dtm.datetime.fromordinal(737447+debd+debf+k) for k in range(n+1-debf)]
dates = [str(k.day)+'/'+str(k.month)+'/'+str(k.year) for k in dates]
lbl = [dtm.datetime.strptime(d,"%d/%m/%Y").date() for d in dates]
for k,l in zip(somcum[debf:],lbl[:-1]):
m = mpat.Rectangle((l.toordinal()+0.5,0),1,k,color='red')
ax.add_patch(m)
plt.annotate(k, (l.toordinal()+1,k), textcoords="offset points",
xytext=(-30,0), ha='center', color='red')
# Affichage de la régression sigmoïdale
dates = [dtm.datetime.fromordinal(737448+debd+debf+k) for k in range(n+dt-debf)]
dates = [str(k.day)+'/'+str(k.month)+'/'+str(k.year) for k in dates]
lbl = [dtm.datetime.strptime(d,"%d/%m/%Y").date().toordinal() for d in dates]
XX = np.array(range(debf,n+dt))
YY2 = f(am,bm,cm)(XX)
plt.plot(lbl,YY2,'--k')
plt.annotate(str(int(round(YY2[-1])))+' ?', (lbl[-1],int(YY2[-1])),
textcoords="offset points", xytext=(0,0),
ha='center', color='black')
plt.annotate(str(int(round(YY2[-dt])))+' ?', (lbl[-dt],int(YY2[-dt])),
textcoords="offset points", xytext=(20,-5),
ha='center', color='black')
YY = f(a,b,c)(XX)
plt.plot(lbl,YY,'-.k')
for k,l in zip(YY[-dt::dt-1],lbl[-dt::dt-1]):
plt.annotate(str(int(round(k)))+' ?', (l,int(k)),
textcoords="offset points", xytext=(0,0),
ha='center', color='black')
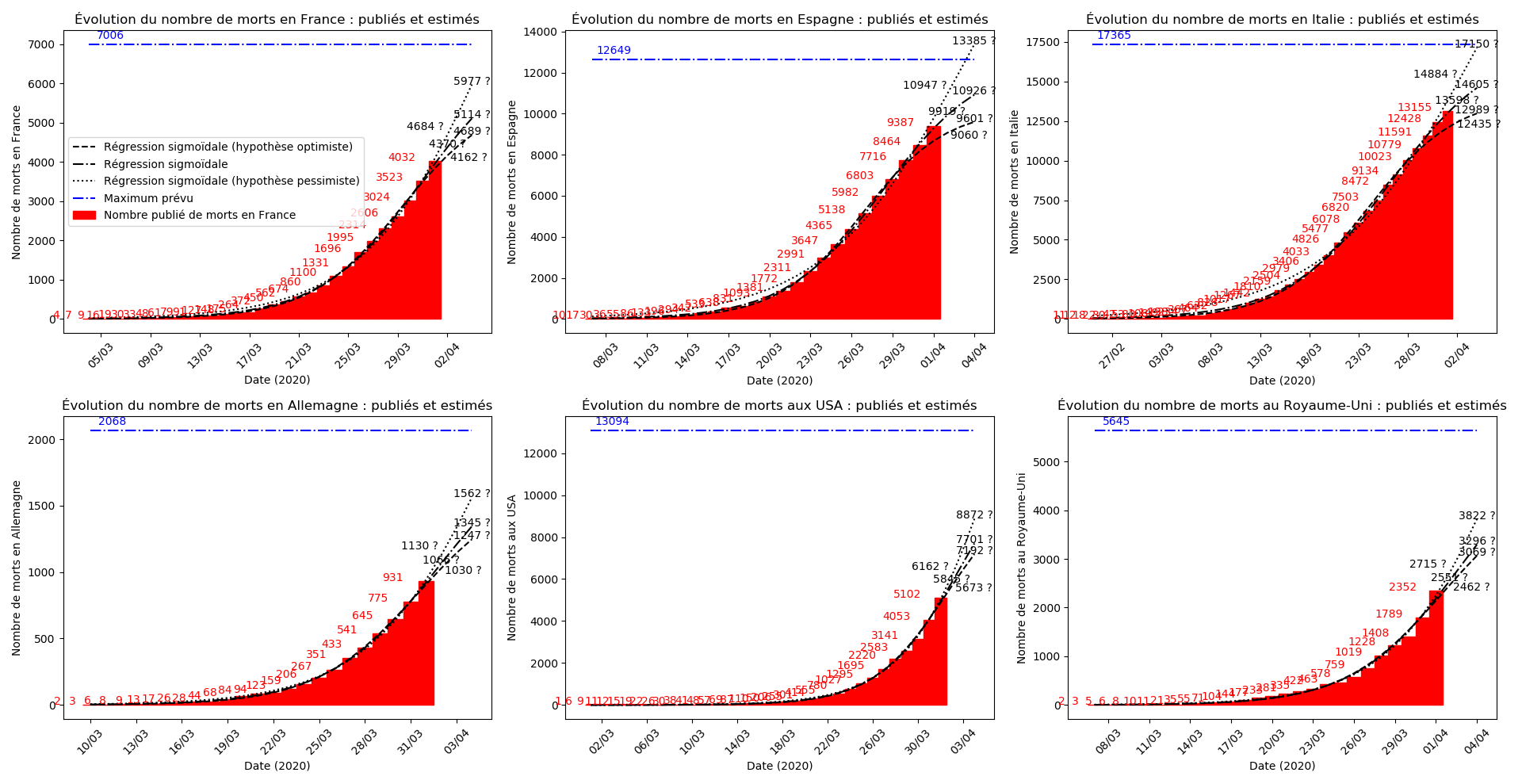
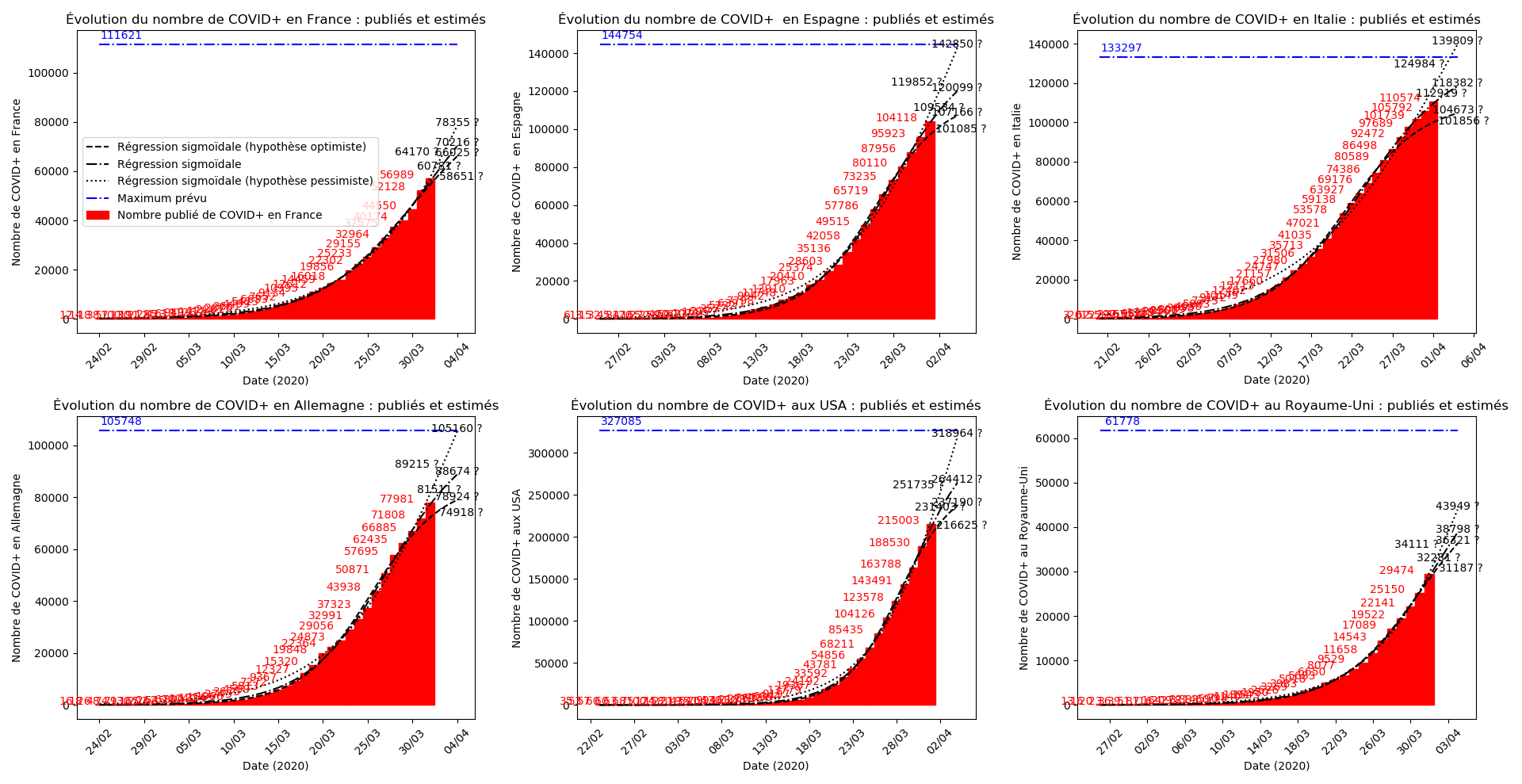
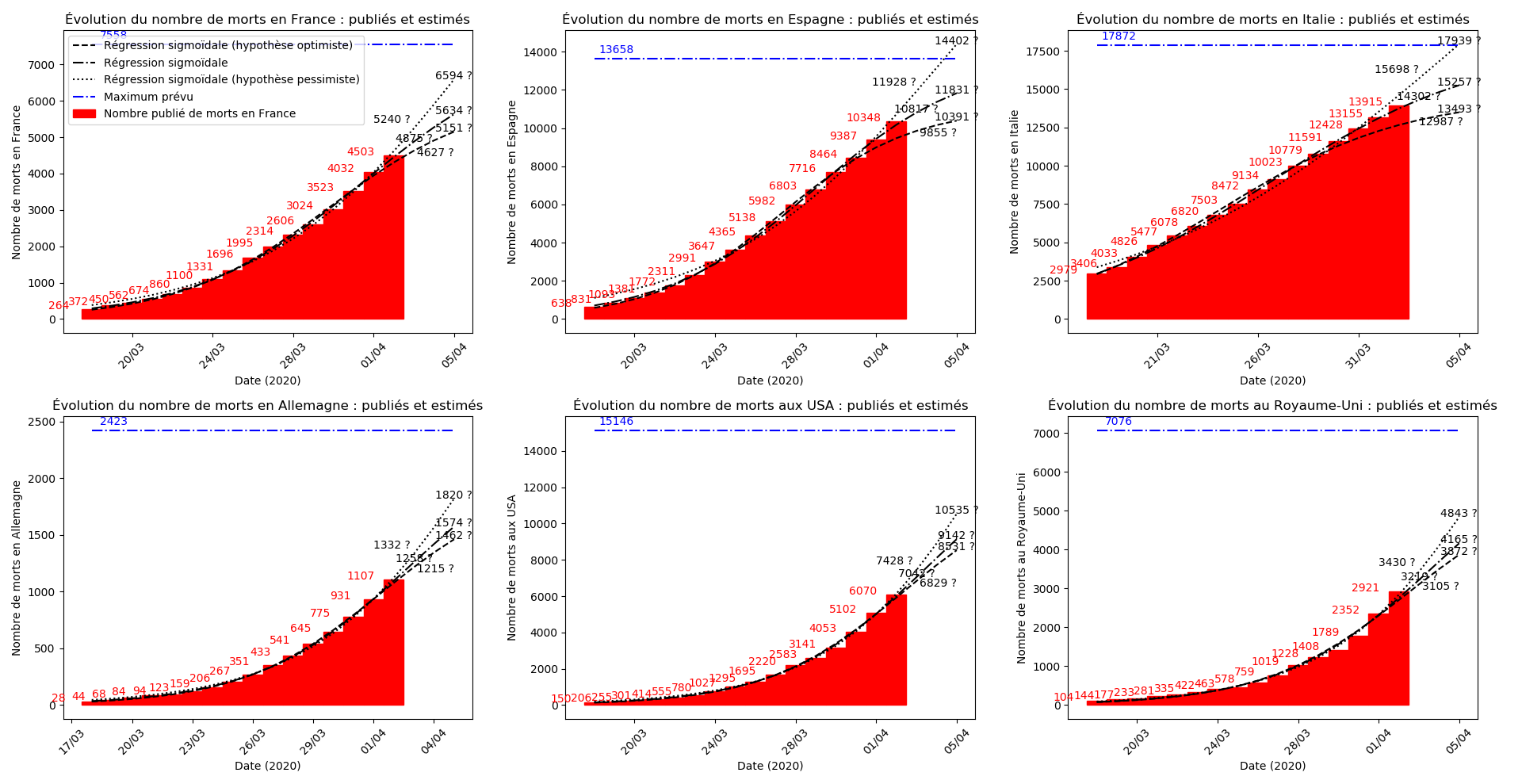
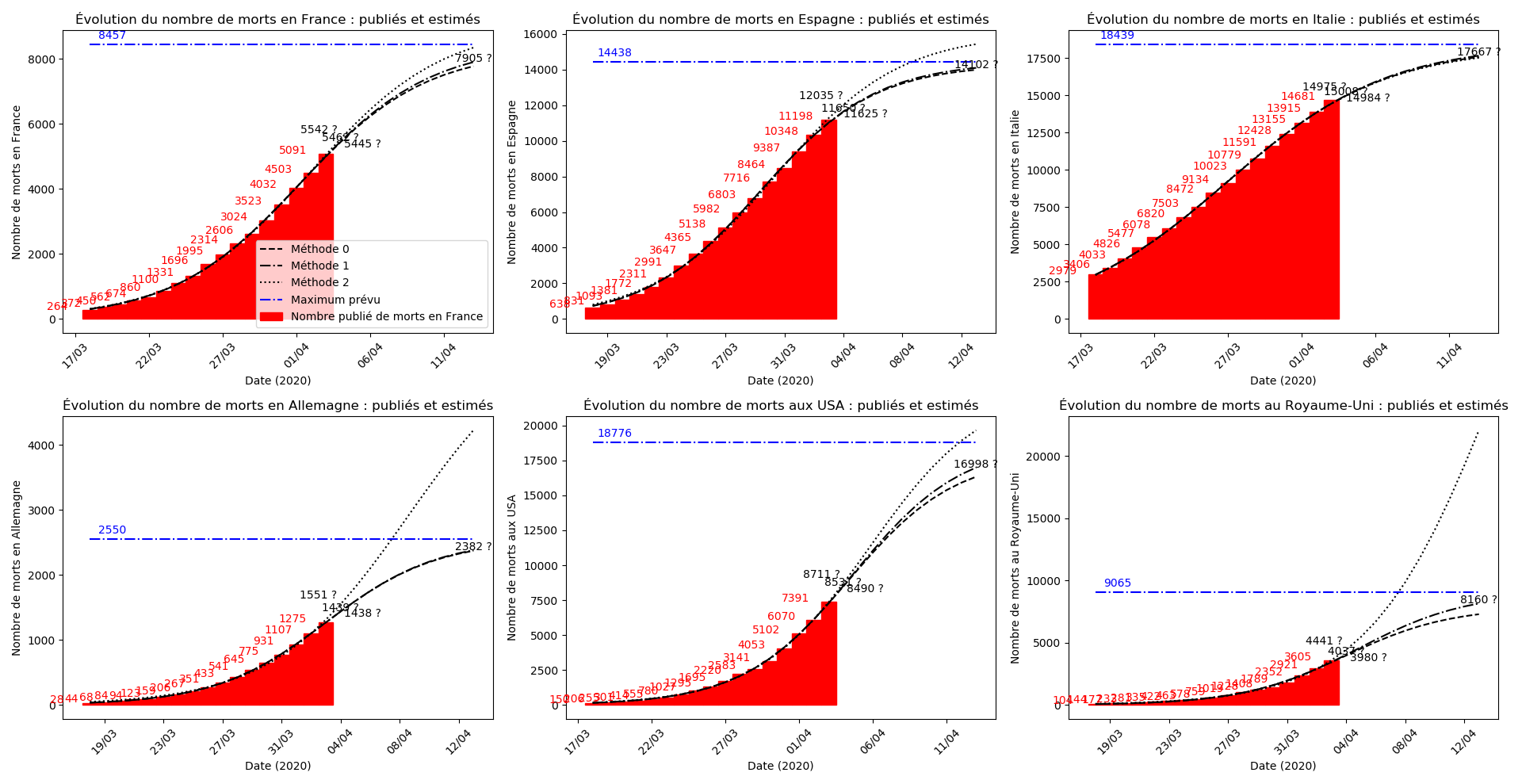
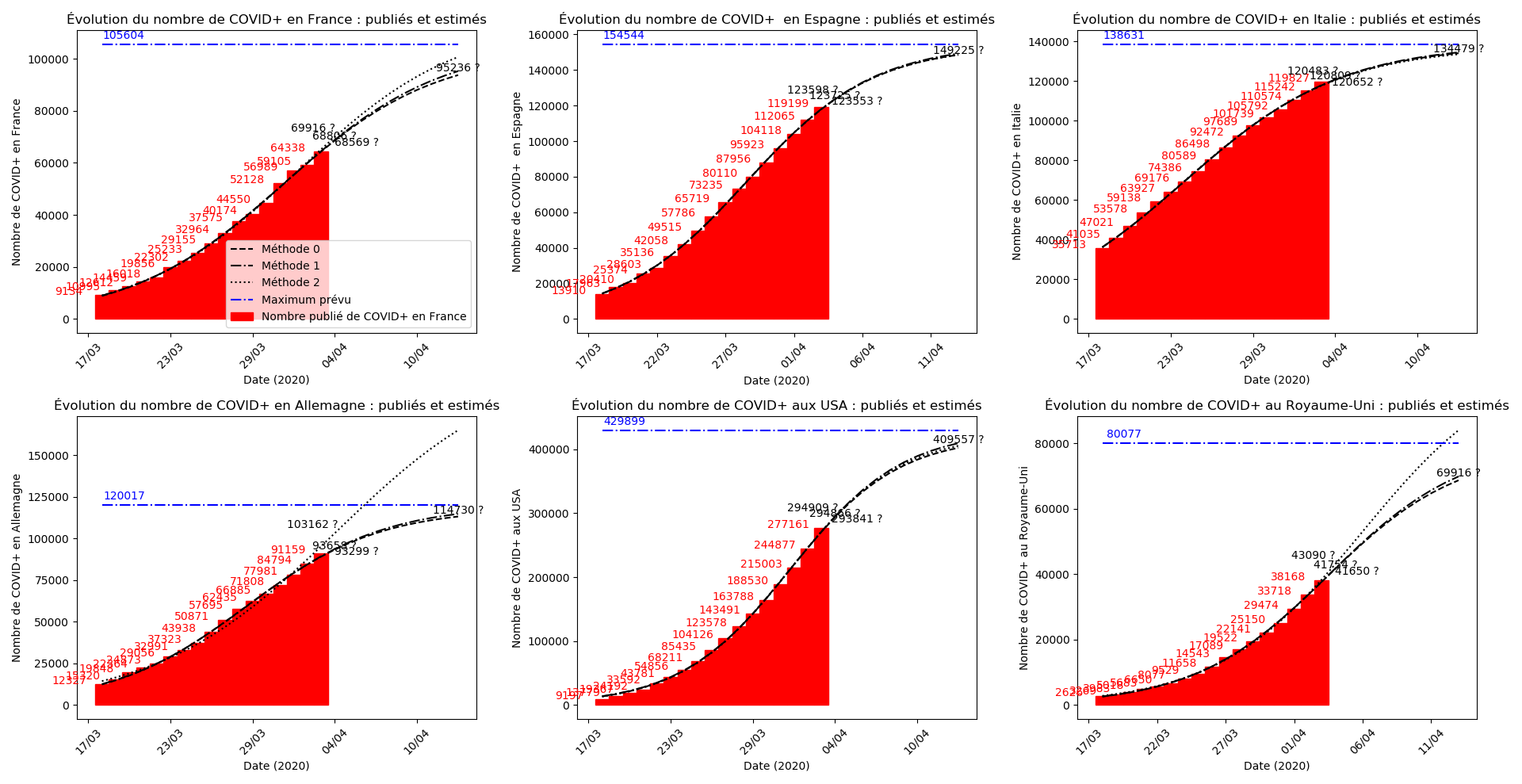
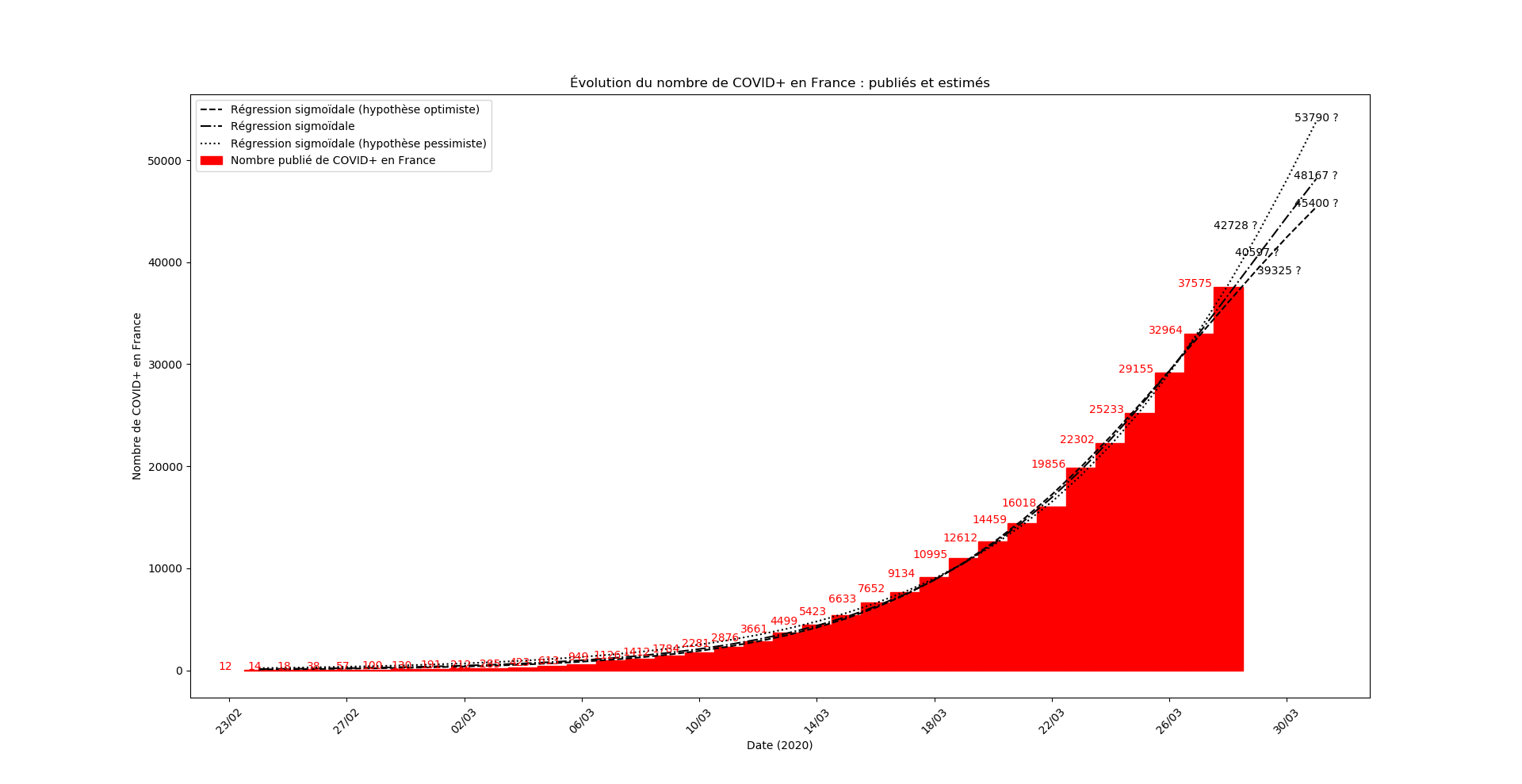
plt.title("Évolution du nombre de "+typeDonnees+" : publiés et estimés")
plt.xlabel("Date (2020)")
plt.ylabel('Nombre de '+typeDonnees)
YY2 = f(aM,bM,cM)(XX)
plt.plot(lbl,YY2,':k')
plt.plot(lbl,0*YY2+c,'-.b')
plt.annotate(str(int(round(c))), (lbl[0],int(c)),
textcoords="offset points", xytext=(20,5),
ha='center', color='blue')
plt.annotate(str(int(round(YY2[-1])))+' ?', (lbl[-1],int(YY2[-1])),
textcoords="offset points", xytext=(0,0),
ha='center', color='black')
plt.annotate(str(int(round(YY2[-dt])))+' ?', (lbl[-dt],int(YY2[-dt])),
textcoords="offset points", xytext=(-20,5),
ha='center', color='black')
plt.xticks(rotation = 45)
if legend:
plt.legend(["Régression sigmoïdale (hypothèse optimiste)",
"Régression sigmoïdale",
"Régression sigmoïdale (hypothèse pessimiste)",
"Maximum prévu",
"Nombre publié de "+typeDonnees])
def repGraph(S0, debutDonnees, debutSimul, finSimul, typeDonnees, nouveaux,
err=1.5, prec=1e-3, typ=[], sbp=None, legend=True, method=1):
# S0 : nombre de cas constatés avant le début des données
# debutDonnees : nombre de jours entre le 22 janvier 2020 et les debut
# des données
# debutSimul : nombre de jours entre le début des données et le début
# de la simulation
# finSimul : nombre de jours entre la fin des données et la fin de la
# simulation
# typeDonnees : chaîne de caractères décrivant les données
# nouveaux : données sous la forme du nombre de nouveaux cas quotidiens
n = len(nouveaux)
debf = debutSimul
debd = debutDonnees
dt = finSimul
La, Lam, LaM = [], [], []
Lb, Lbm, LbM = [], [], []
Lc, Lcm, LcM = [], [], []
for fin in range(debf,n+1):
((am,bm,cm),(a,b,c),(aM,bM,cM)) = interpSigm(nouveaux,fin,S0=S0,
mxS=7e7, err=err,
prec = prec,
method = method)
La.append(a)
Lam.append(am)
LaM.append(aM)
Lb.append(b)
Lbm.append(bm)
LbM.append(bM)
Lc.append(c)
Lcm.append(cm)
LcM.append(cM)
dates = [dtm.datetime.fromordinal(737447+debd+k) for k in range(debf,n+1)]
if (not typ)or(0 in typ):
evol(dates,(Lam,La,LaM),
"Evolution du paramètre a de l'interpolation avec le temps",
typeDonnees, sbp=sbp, legend=legend)
if (not typ)or(1 in typ):
evol(dates,(Lbm,Lb,LbM),
"Evolution du paramètre b de l'interpolation avec le temps",
typeDonnees, sbp=sbp, legend=legend)
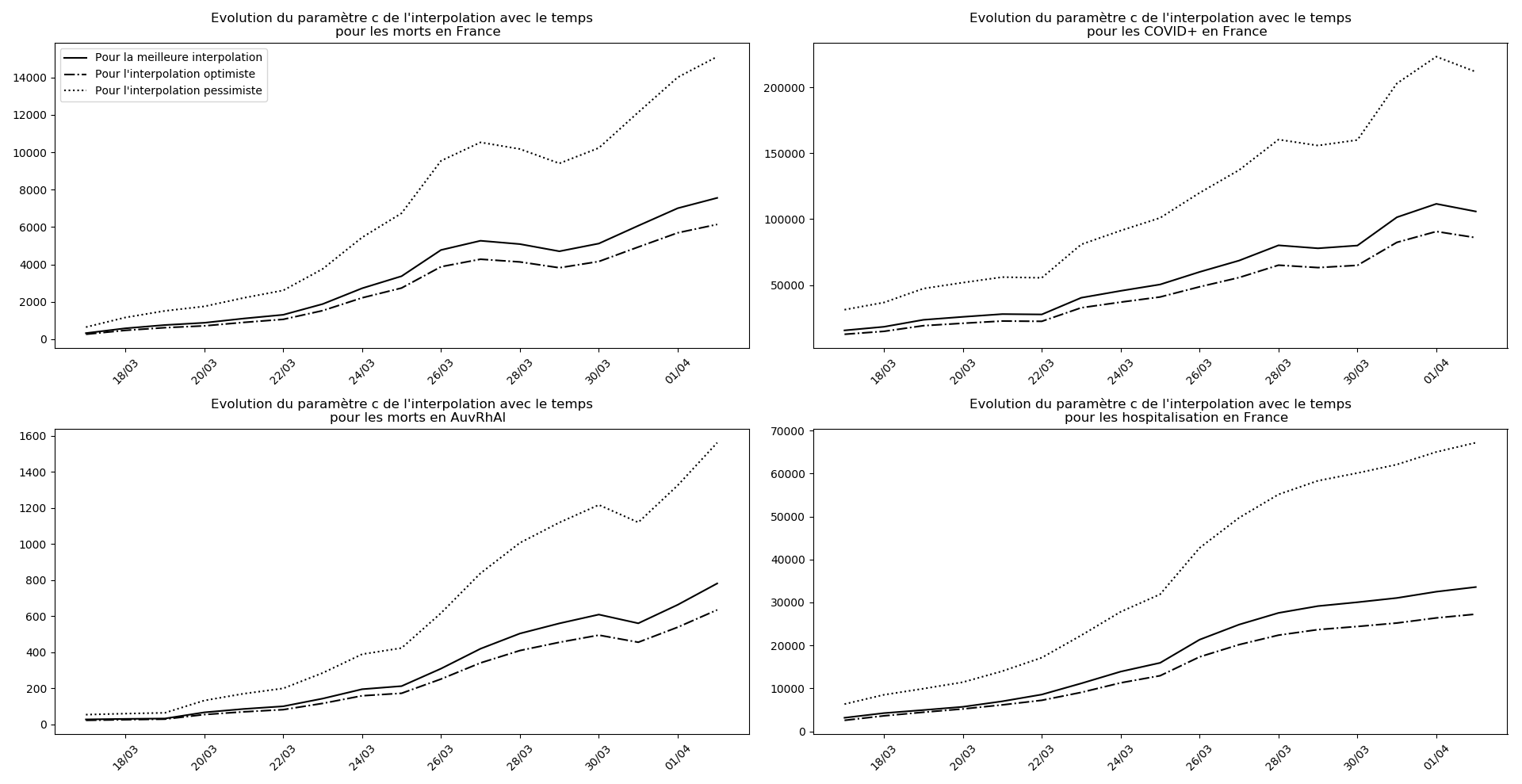
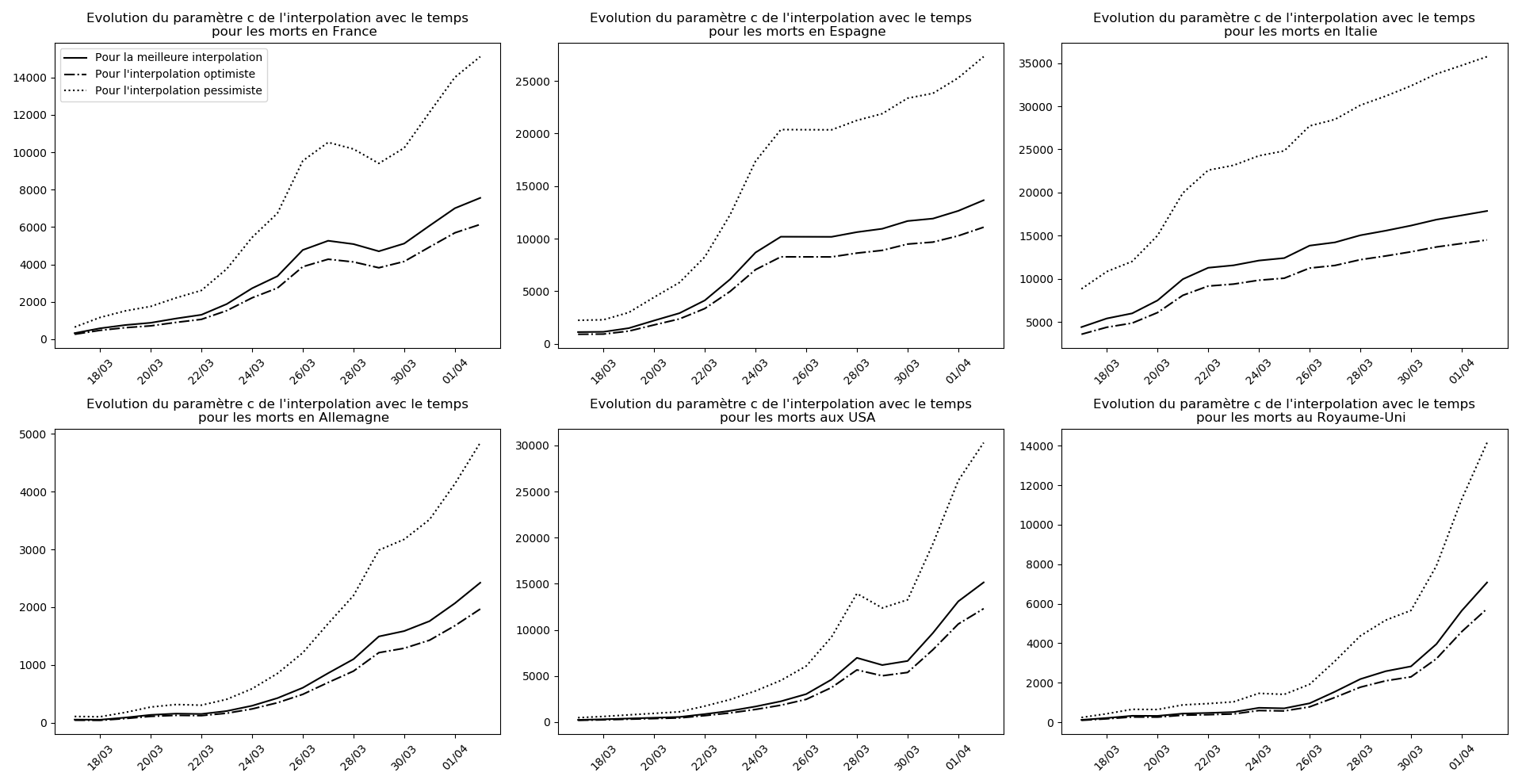
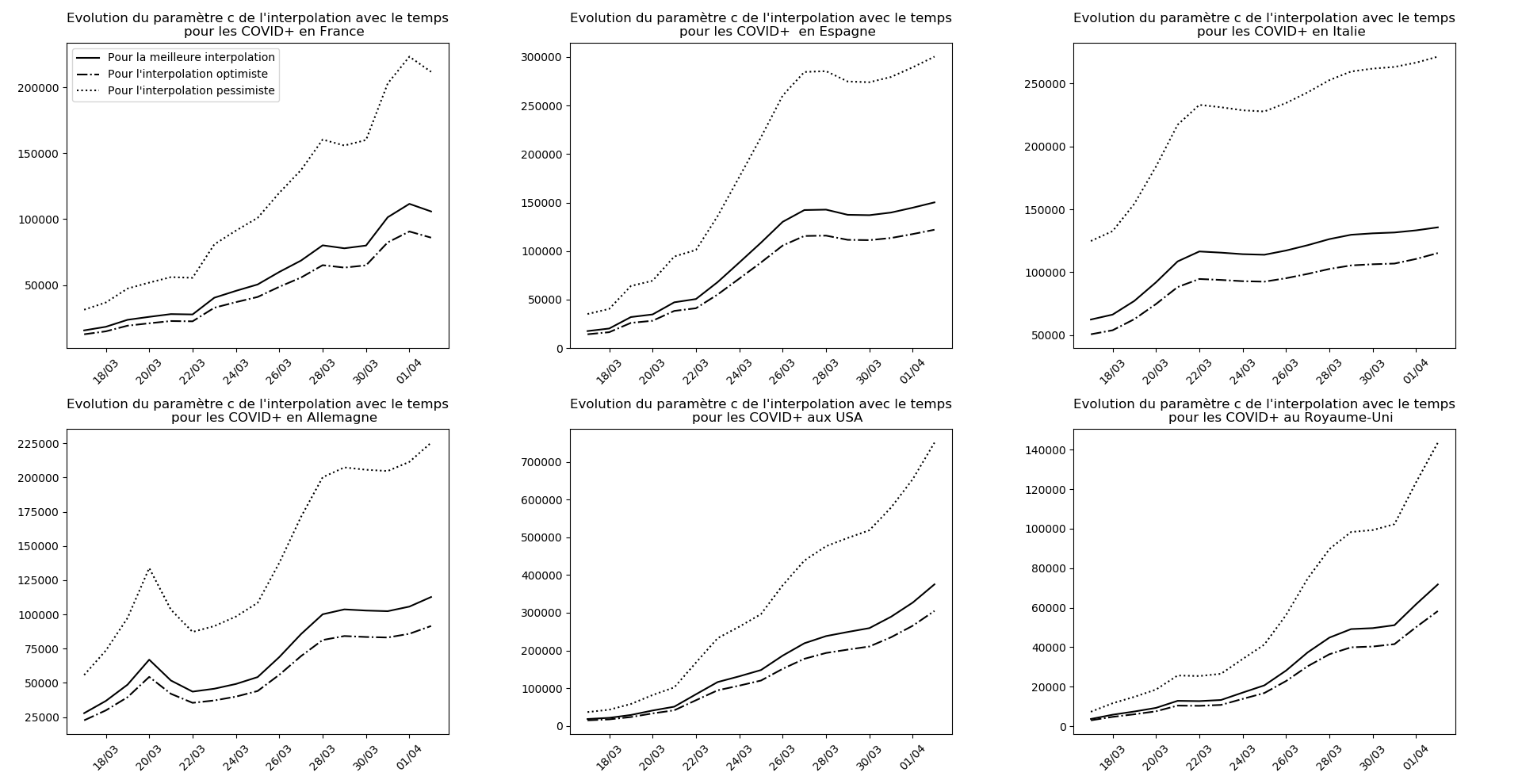
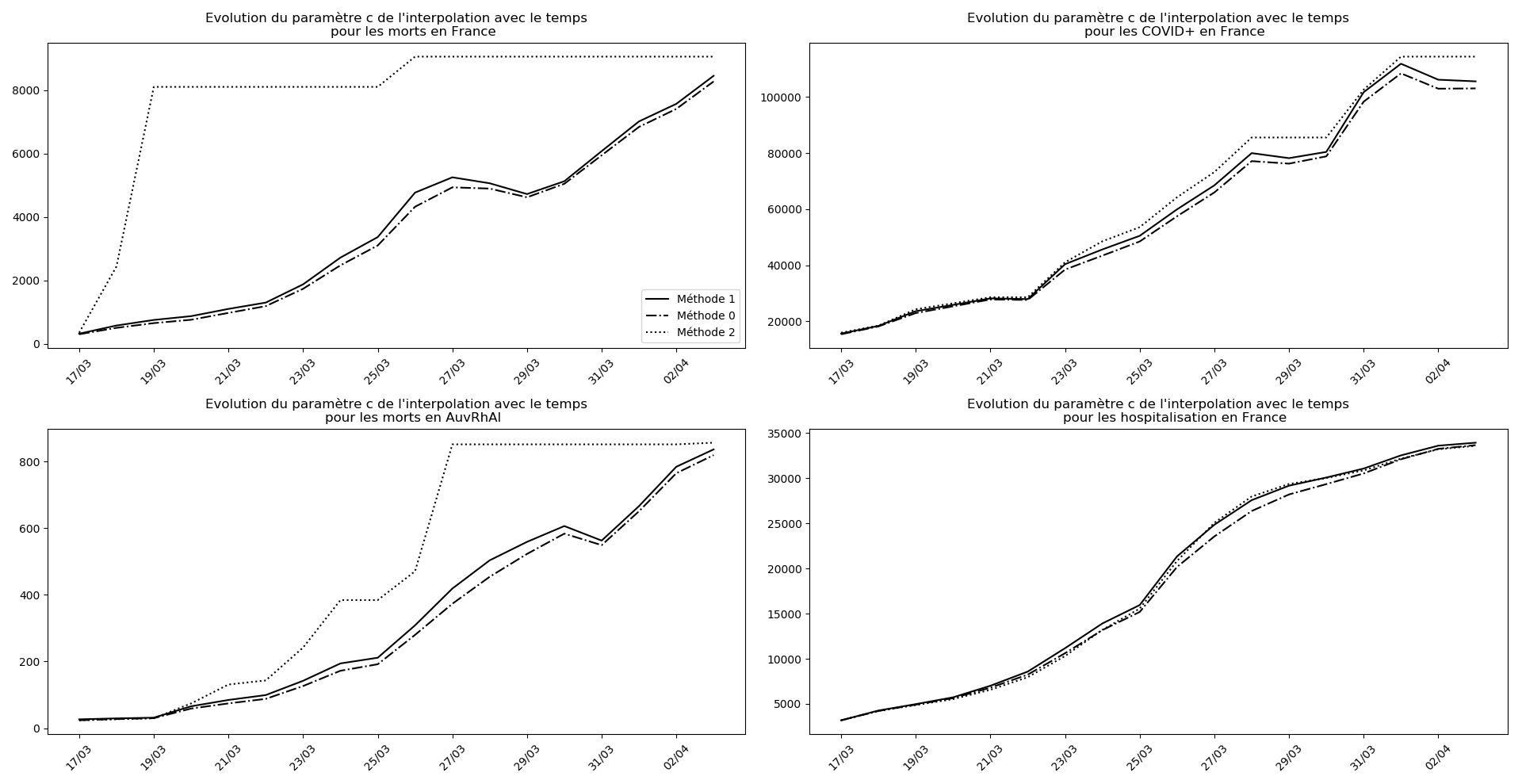
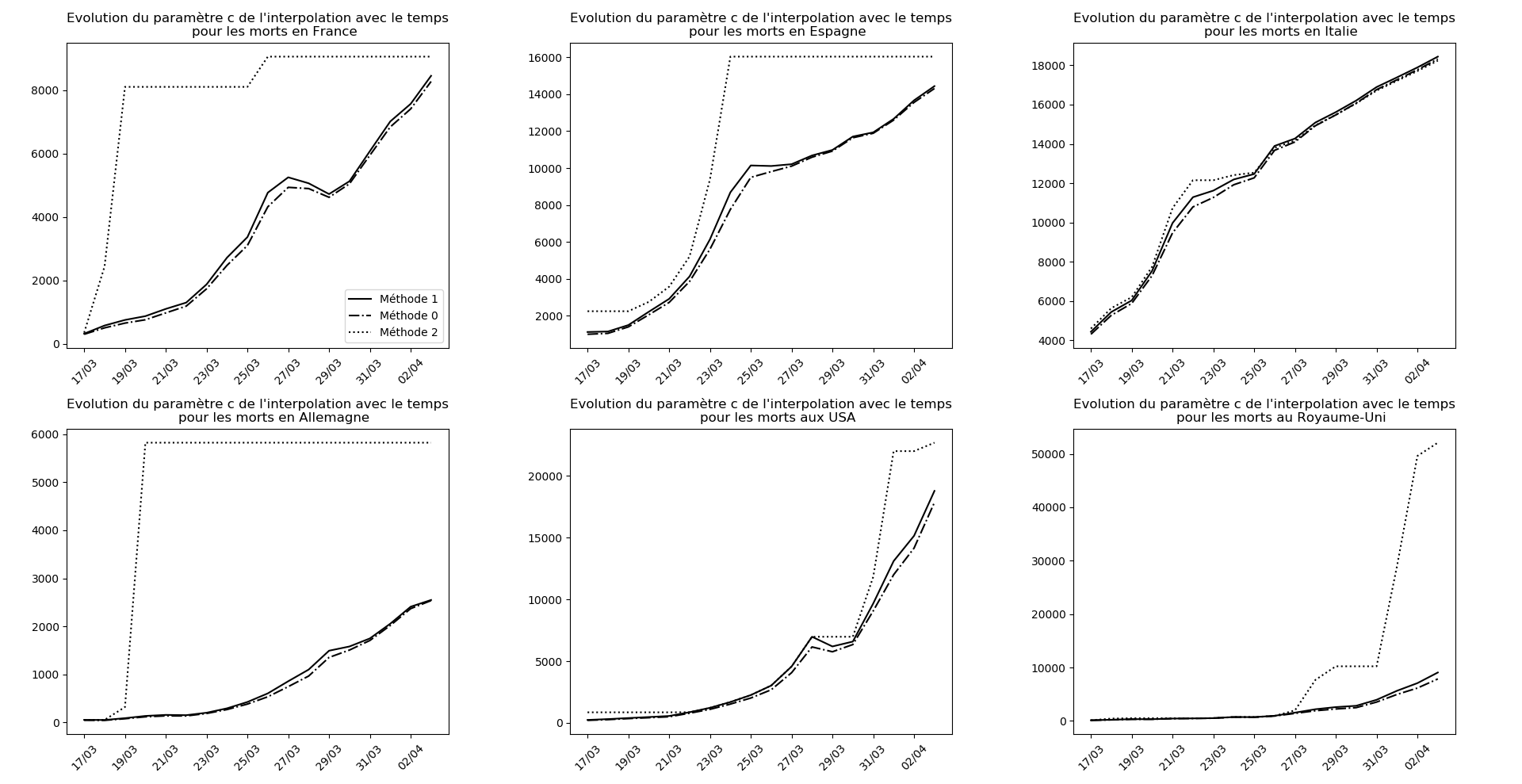
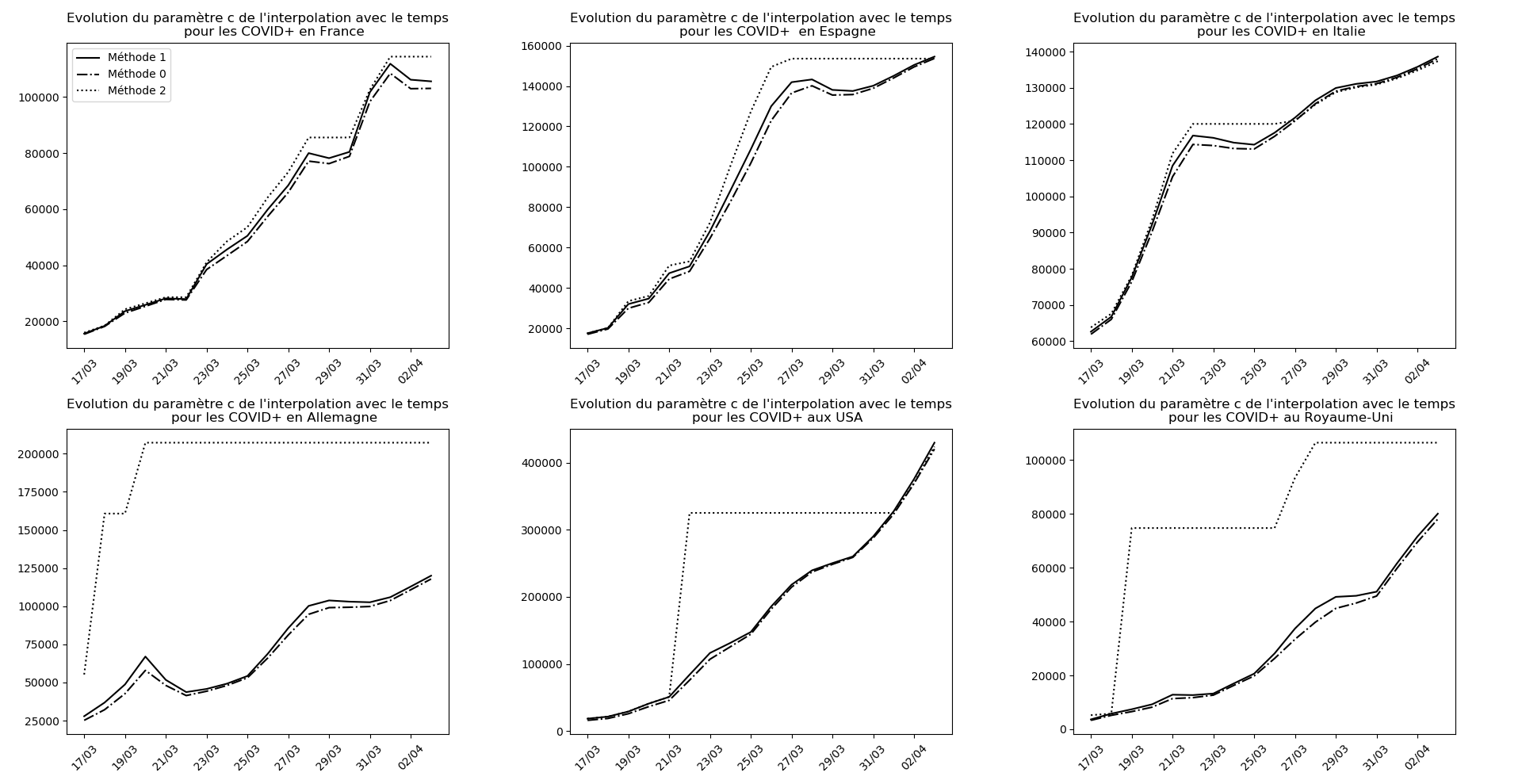
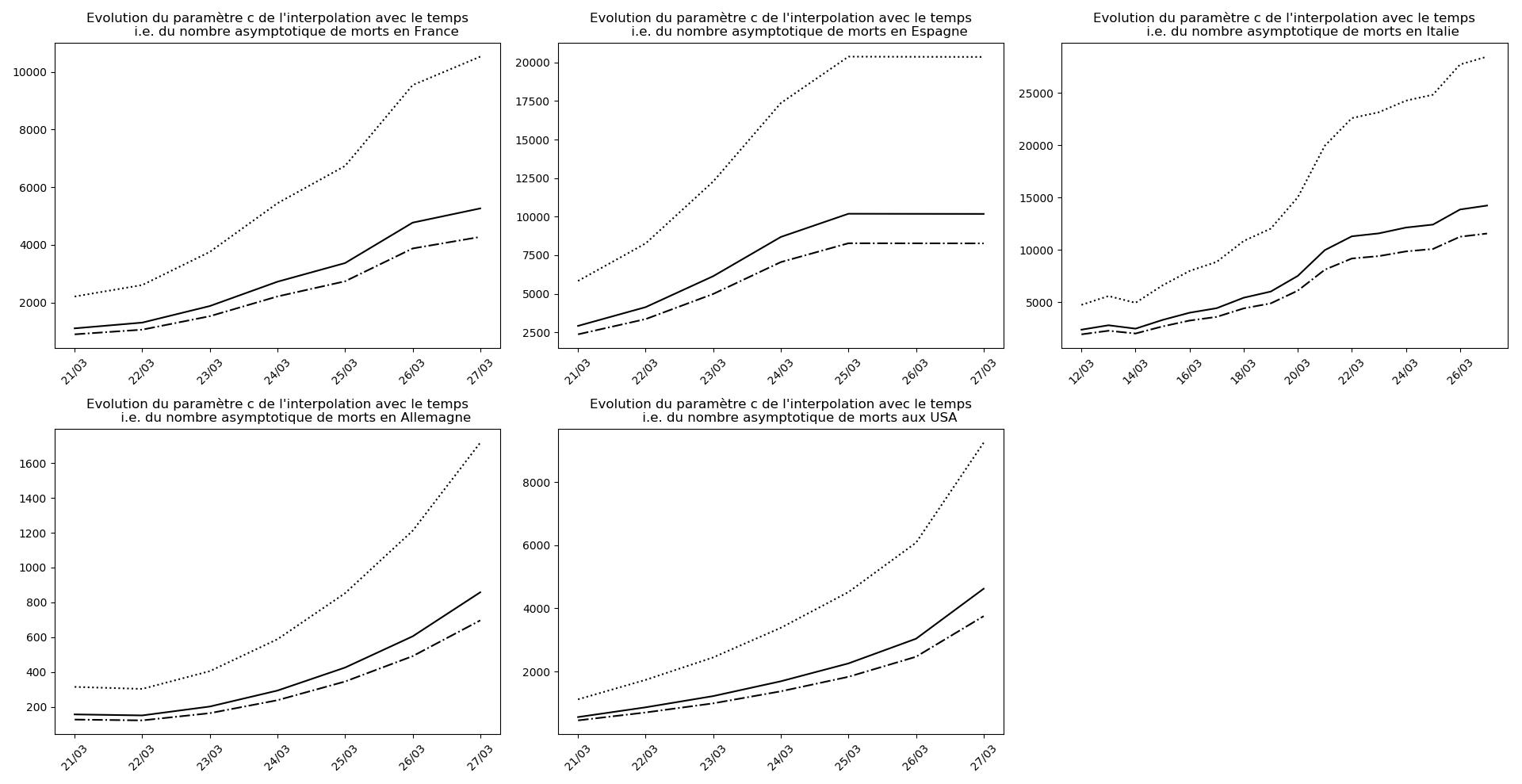
if (not typ)or(2 in typ):
evol(dates,(Lcm,Lc,LcM),
"Evolution du paramètre c de l'interpolation avec le temps",
typeDonnees,sbp=sbp, legend=legend)
carac = [caracteristiques(La[i],Lb[i],Lc[i],debf+i) for i in range(n-debf+1)]
T1 = [k[0] for k in carac]
T2 = [k[1] for k in carac]
T3 = [dtm.datetime.fromordinal(int(round(k[2]))+737448+debd) for k in carac]
if (not typ)or(3 in typ):
evol_taux(dates, T1, T2,typeDonnees, sbp=sbp, legend=legend)
if (typ is None)or(4 in typ):
evol_inflexion(dates, T3,typeDonnees, sbp=sbp)
somcum = [S0+sum(nouveaux[:(k+1)]) for k in range(n)]
if (not typ)or(5 in typ):
evol_previsions(dates, (Lam,La,LaM,Lbm,Lb,LbM,Lcm,Lc,LcM), nouveaux,
somcum, debf, typeDonnees,sbp=sbp, legend=legend)
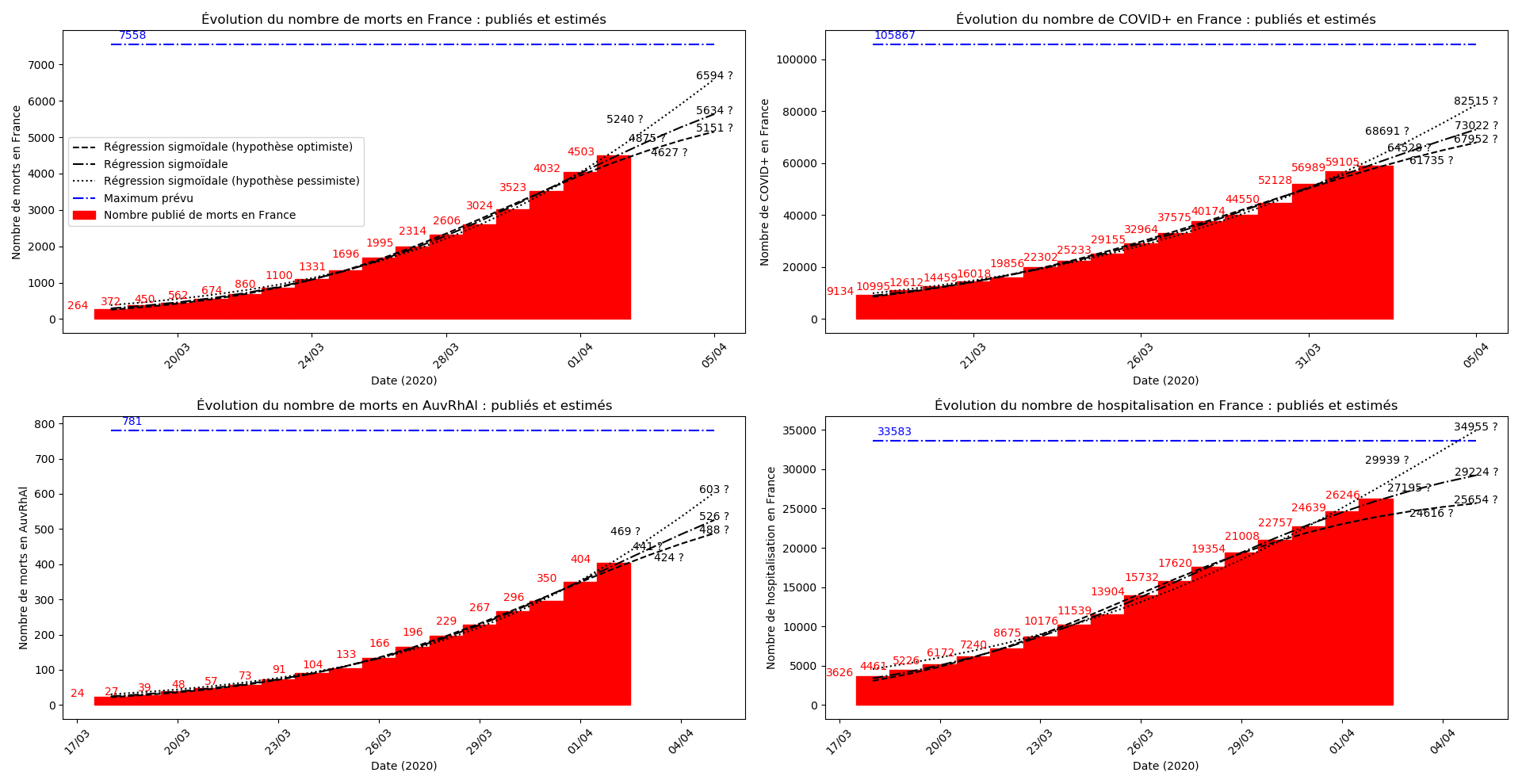
if (not typ)or(6 in typ):
evol_cas(dates, (am,a,aM,bm,b,bM,cm,c,cM), somcum, debd, debf, dt,
typeDonnees, sbp=sbp, legend=legend)
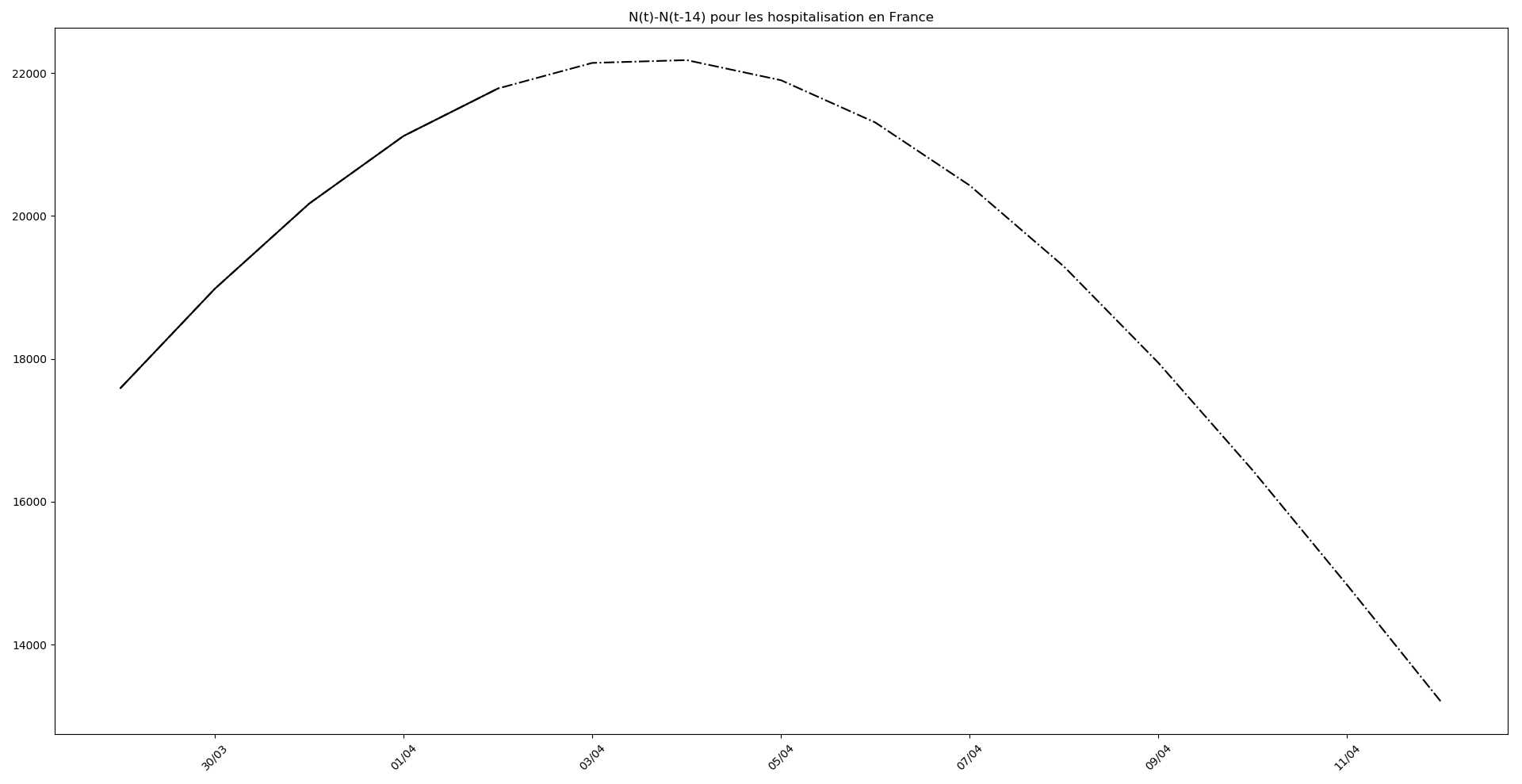
if (not typ)or(7 in typ):
evol_pic(debd, dt,n,a,b,c,typeDonnees, sbp=sbp)
class covid():
def __init__(self,datas):
self.datas = [list(datas)]
def add(self,datas):
self.datas.append(list(datas))
def setDt(self,dt):
for k in self.datas:
k[3] = dt
def repGraph(self, k, typ=[], err=1.5, method = 1, prec = 1e-5):
repGraph(*self.datas[k],typ=typ, method = method, err=err, prec=prec)
def compare(self,typ, which=None, err=1.5, method = 1, prec = 1e-5):
fig = plt.figure()
plt_set_fullscreen()
fig.set_tight_layout(True)
assert isinstance(typ,int) and 0<=typ<=7, "typ doit être un entier"
n = len(self.datas)
if not which:
which=range(n)
n = len(which)
p = int(np.sqrt(n+1))
a = p*100 + (n//p+(n%p>0))*10
for k in range(len(which)):
repGraph(*self.datas[which[k]], typ=[typ],sbp=a+k+1,legend=(k==0),
err = err, method = method, prec = prec)
Utilisation
Pour utiliser l’algorithme, il suffit de déclarer un objet de la classe covid de la façon suivante :
Cov = covid((4, # nombre de cas avant la série de données
40, # nombre de jours entre le 22 janvier et le premier jour de la série
18, # nombre de jours entre le 1er jour de la série et le début de la simul
3, # nombre de jours simulés après la fin de la série
"morts en France", # chaine représentant la série
[0, 3, 2, 7, 3, 11, 3, 15, 13, 18, 12, 36, 21, 27, 89, 108, 78, 112,
112, 186, 240, 231, 365, 299]))
Puis d’utiliser l’une des méthodes de la classe permettant de faire des représentations graphiques.
Exemples
Sources des données : https://www.worldometers.info/coronavirus/
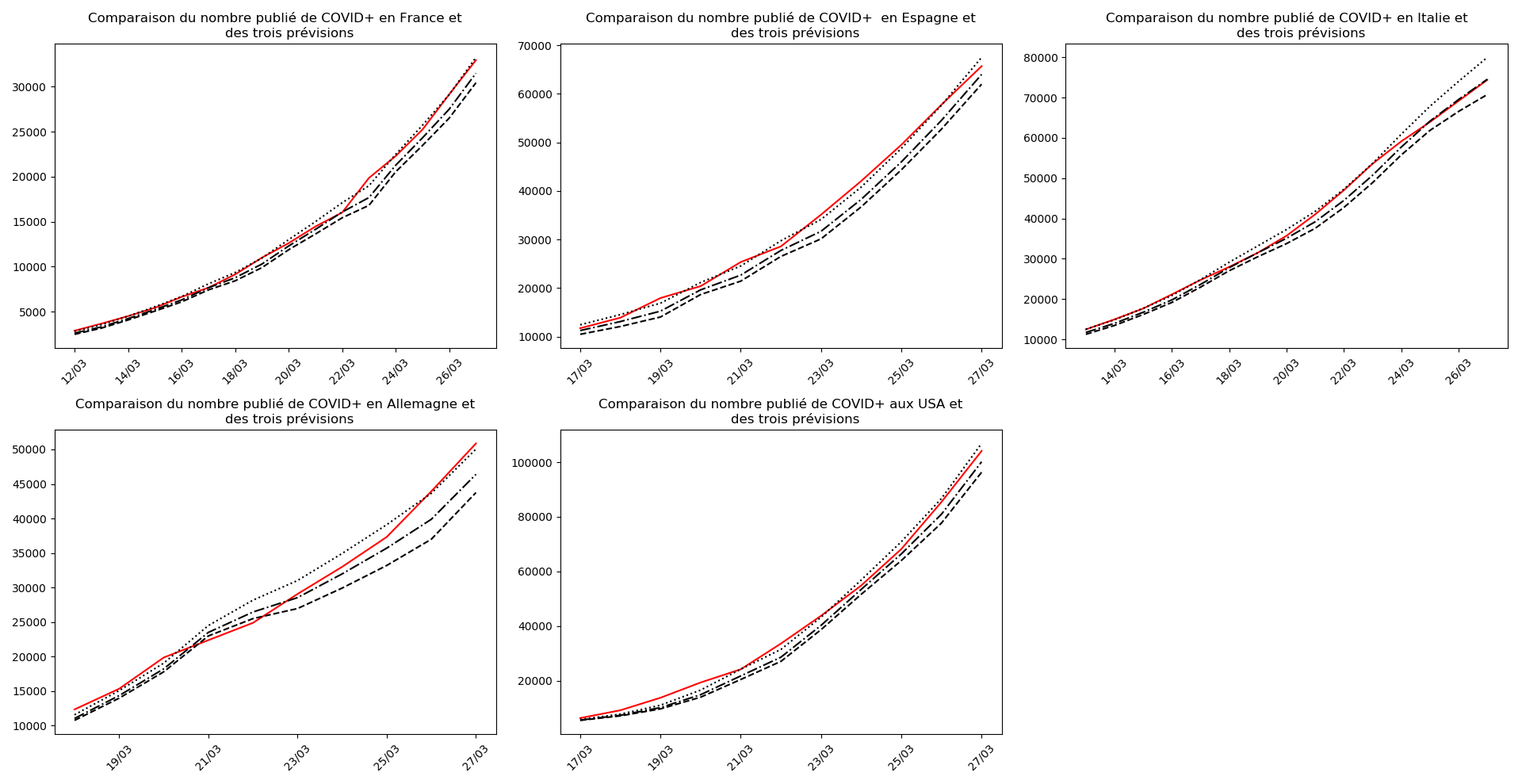
Situation au 28 mars
L’Espagne et l’Italie semblent en train de se sortir d’affaire. J’expliquerai un autre jour ce qui permet de lire, sur les graphiques, les signes de la fin d’épidémie.
Source des données : https://www.worldometers.info/coronavirus/
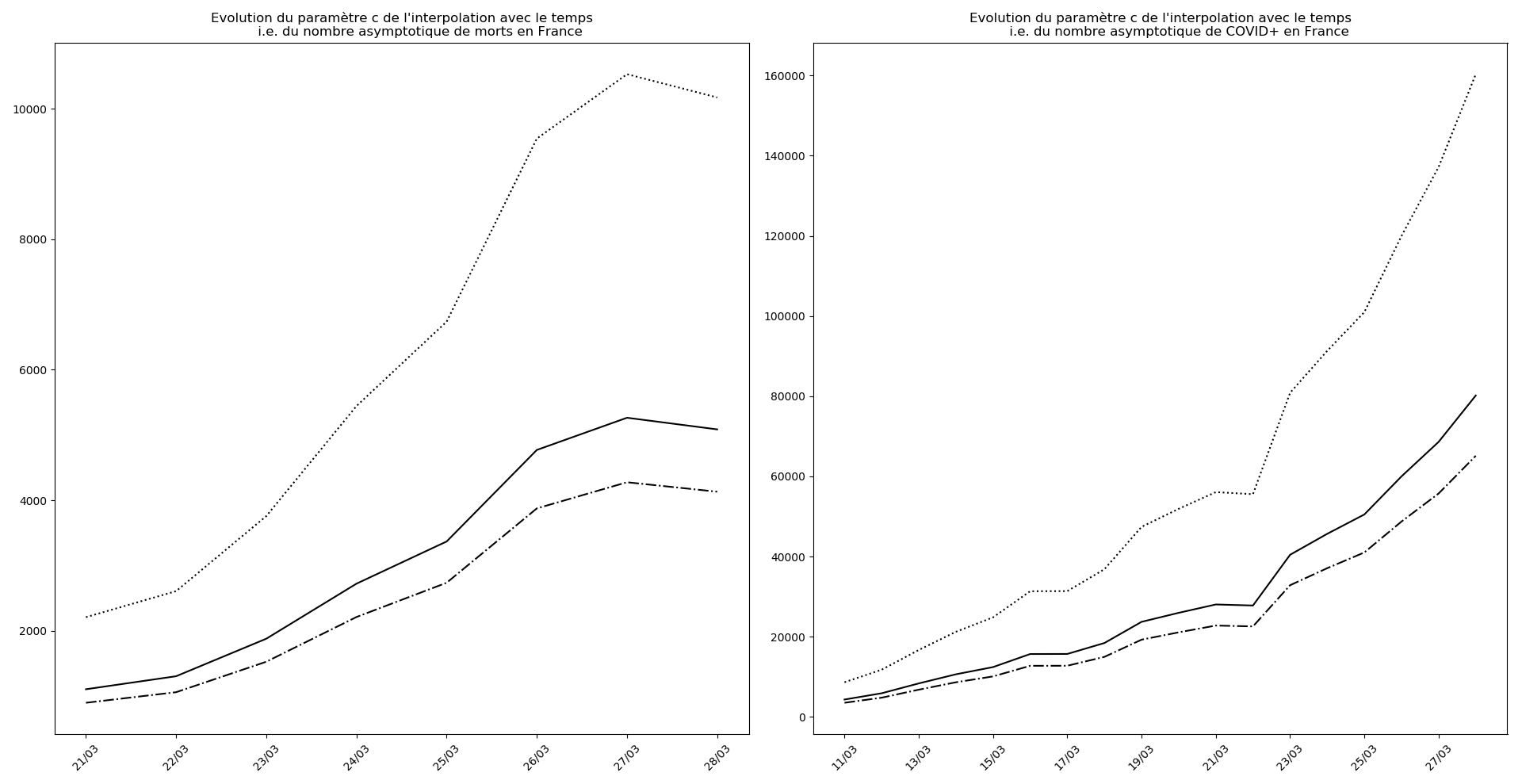
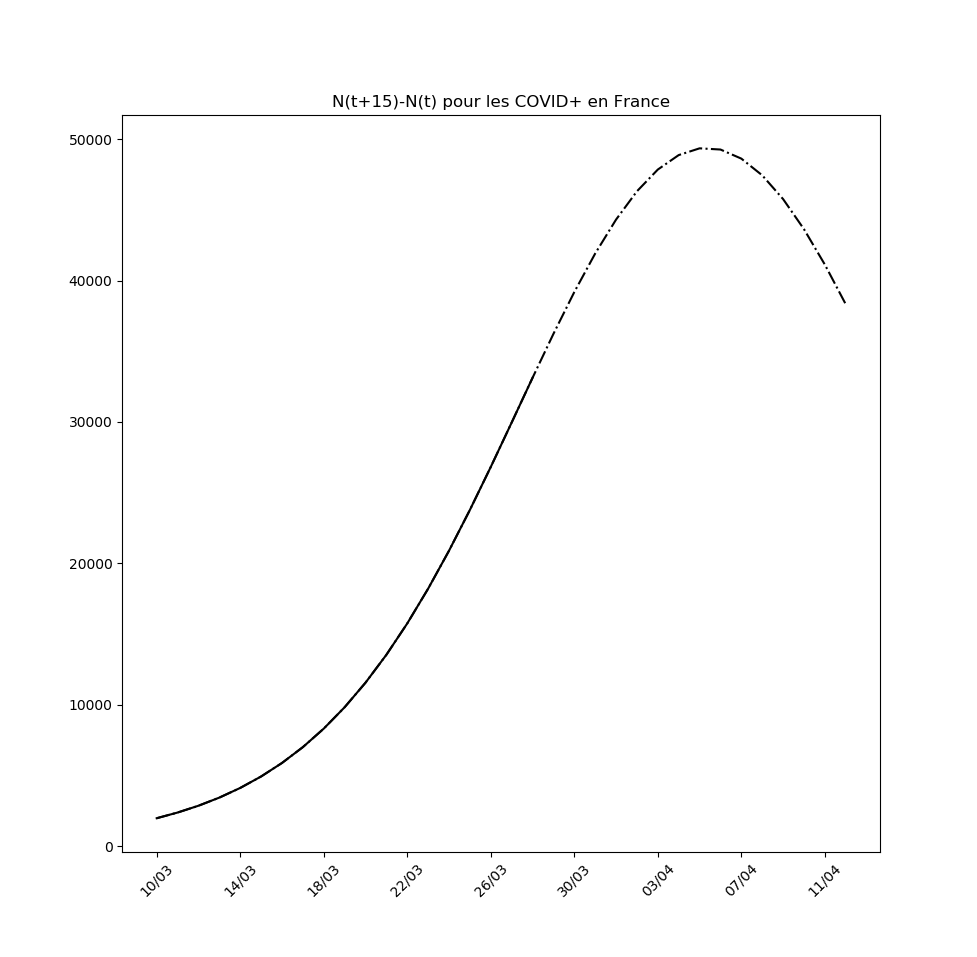
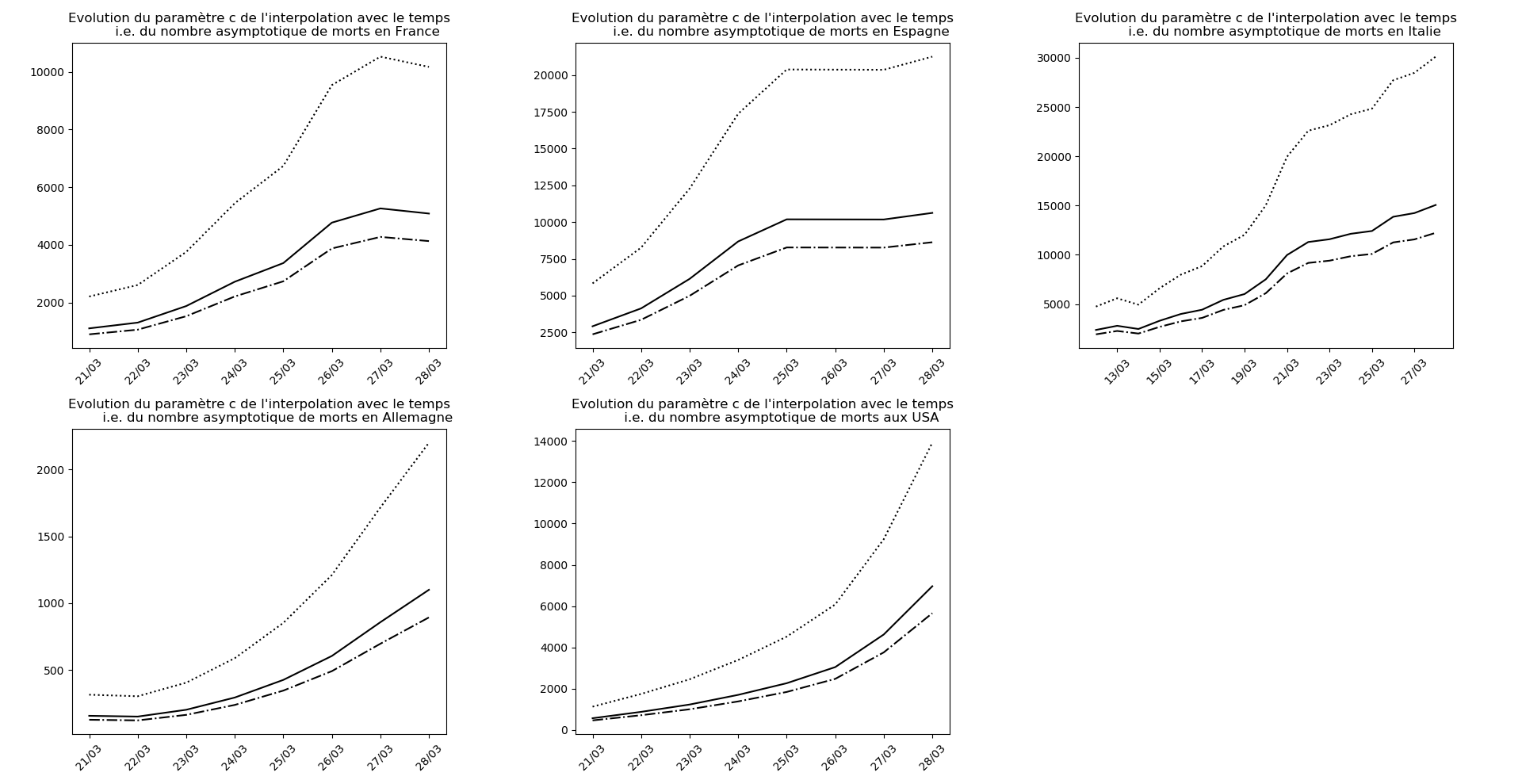
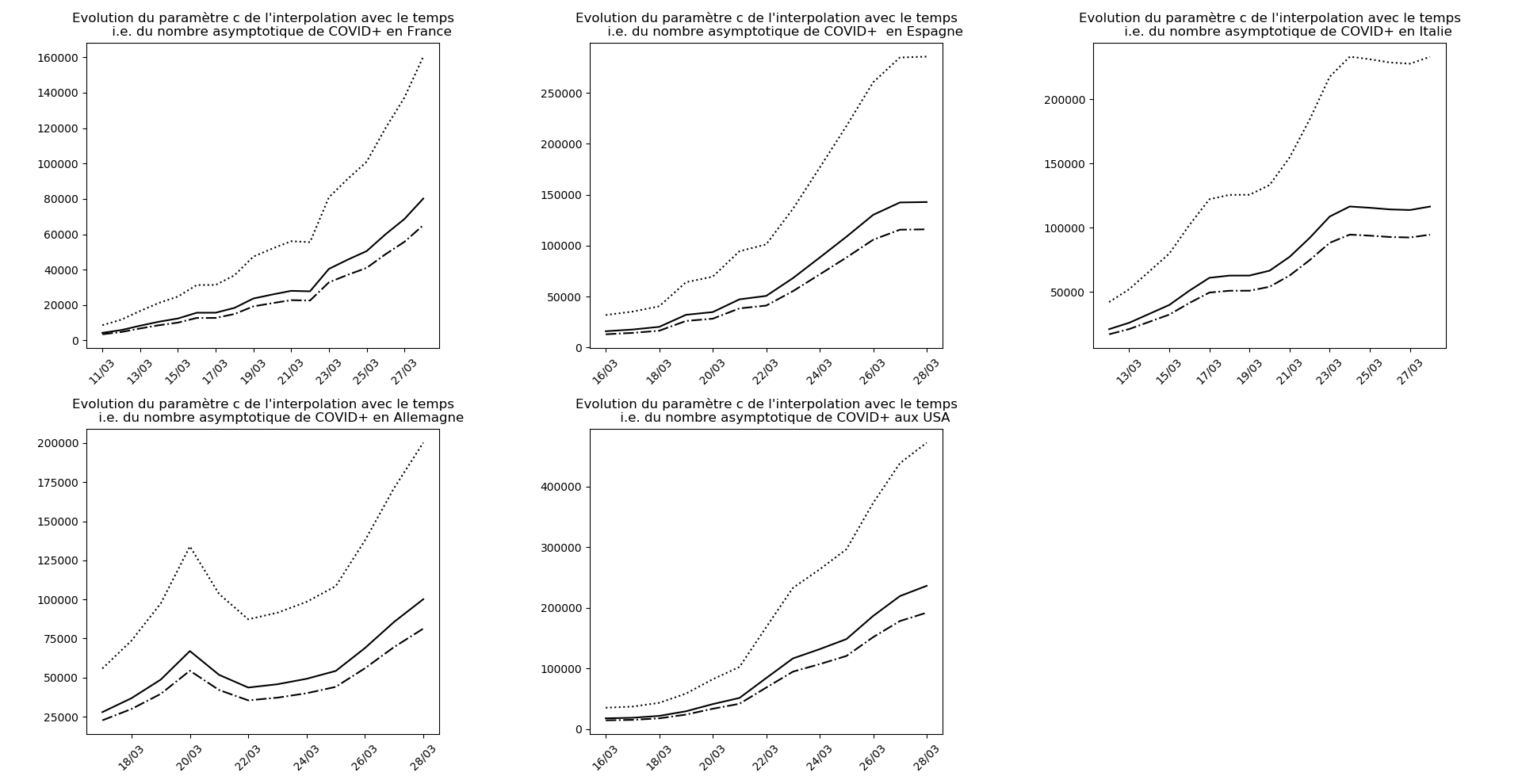
Le pic pourrait arriver aux environs du 31 mars pour l’Italie et du 5 avril pour l’Espagne.
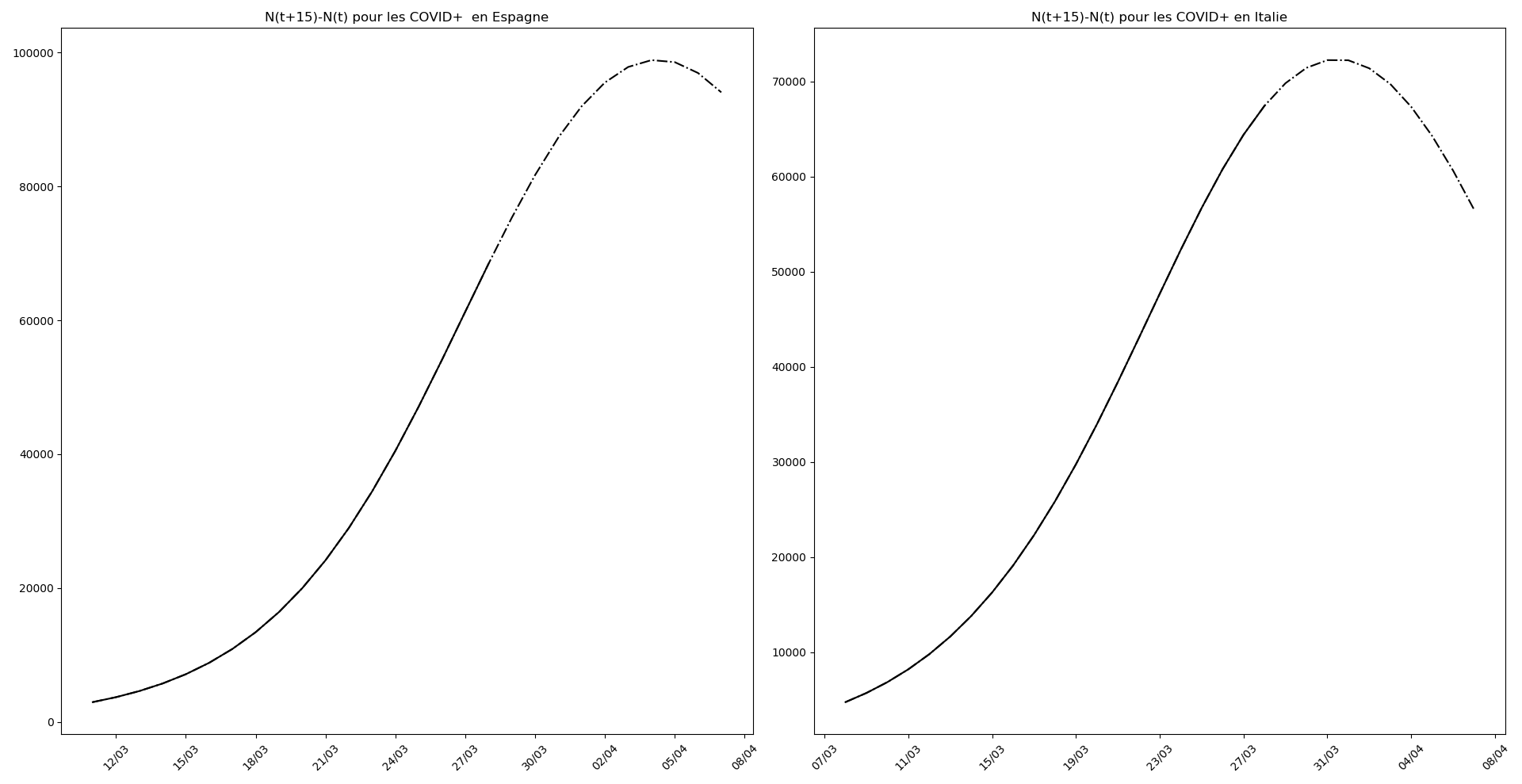
Situation au 1er avril
Je m’étais déjà aperçu que l’Allemagne publie deux bulletins de situation : un le soir, largement sous-estimé, puis une mise-à-jour dans la nuit… Je viens de me rendre compte que l’Espagne fait la même chose ! Tous les graphiques que j’ai publiés depuis 3 jours étaient faux. J’ai supprimé les mises-à-jour correspondantes et j’ai corrigé les graphiques ci-dessous…
J’ai remplacé les données pour Auvergne-Rhône-Alpes par celles pour le Royaume-Uni.
Malgré cette révision à la hausse des statistiques que j’avais pour l’Espagne, il n’en demeure pas moins que l’Italie semble avoir passé le pic de l’épidémie et que l’Espagne devrait le passer le 4 avril… autant dire qu’elle y est vues les énormes approximations de ce modèle.
Il se pourrait que l’Allemagne n’en soit pas loin (voir ce graphique et la convergence apparente du nombre asymptotique de CoViD+ par exemple, qui est un signe de franchissement du point d’inflexion).
Pour la France, il faut attendre, notamment la situation est assez sombre en Auvergne-Rhône-Alpes.
Source des données :
- pour le monde : https://www.worldometers.info/coronavirus/
- pour Auvergne-Rhône-Alpes : https://www.auvergne-rhone-alpes.ars.sante.fr/liste-communiques-presse
Situation au 2 avril
France
Le nombre de CoViD+ n’est plus donné pour les régions. Le nombre d’hospitalisations, que le gouvernement a l’air de considérer comme la seule statistique valable n’est fourni officiellement que depuis le 18 mars… Difficile de suivre cette improvisation permanente.
Pas de stabilisation apparente de la situation. Il faut attendre. Notamment, la situation en Auvergne-Rhône-Alpes est en pleine phase croissante.
Allez, une petite perspective positive quand même : si on ne regarde que le nombre d’hospitalisations, le pic épidémique pourrait être tout proche.
Sources des données :
- https://dashboard.covid19.data.gouv.fr/
- https://www.auvergne-rhone-alpes.ars.sante.fr/liste-communiques-presse
Monde
La situation en Italie continue à s’améliorer, l’espoir est vraiment là. Le pic épidémique semble passé, les hôpitaux devraient commencer à se désengorger.
Pour l’Espagne aussi, le pic épidémique est là. Les prochains jours devraient apporter une véritable amélioration.
Pour l’Allemagne, l’épidémie est contenue mais reste cependant active. Difficile de comprendre ce qui s’y passe (au moins pour moi).
Le Royaume-Uni et les USA sont dans une situation vraiment sombre…
Source des données :
Situation au 3 avril
J’ai modifié l’algorithme en utilisant 3 méthodes différentes pour l’interpolation plutôt que des versions optimistes et pessimistes qui n’étaient pas vraiment fondées sur le plan théorique. Pour le reste, pas de commentaires aujourd’hui, les graphiques parlent d’eux-mêmes.
France
Sources des données :
- https://dashboard.covid19.data.gouv.fr/
- https://www.auvergne-rhone-alpes.ars.sante.fr/liste-communiques-presse
Monde
Source des données :