Cet article a pour but de détailler, en se concentrant sur l’exemple de la fonction exponentielle complexe, les propriétés des transformations conformes. Le début est peut-être un peu indigeste et manque d’illustrations… mais il y a de belles images et exemples de codes Python pour les faire soi-même à la fin.
Un peu de vocabulaire
Le terme de transformation est un synonyme, en mathématiques, du terme bijection : il s’agit d’une fonction entre deux ensembles telle que tout élément du second ensemble possède un, et un seul, antécédent dans le premier ensemble. Une des dénominations anglaises pour cette notion est one-to-one-mapping qui est probablement plus parlante.
Par ailleurs, le terme de transformation s’utilise pour les fonctions entre ensembles géométriques.
On dit d’une transformation qu’elle est conforme si elle préserve, localement, les angles.
Parmi les transformations conformes, il y a donc les isométries qui préservent non seulement les angles, mais aussi les longueurs. Ou plus généralement les similitudes qui multiplient toutes les longueurs par un réel donné, appelé rapport de similitude.
Enfin, on dit d’une similitude qu’elle est directe si elle préserve les angles orientés.
Pour en savoir plus sur les similitudes, notamment pour comprendre que l’on peut facilement les classifier, on pourra se rapporter à l’article de Wikipedia sur le sujet.
Similitudes directes du plan complexe
Intéressons plus précisément aux similitudes directes de $\mathbf{C}$, c’est-à-dire aux fonctions du plan complexe dans lui-même multipliant les longueurs par un réel strictement positif et préservant les angles orientés. Par théorème de classification, on peut affirmer que
- du point de vue géométrique, ce sont exactement les translations, les rotations ou les composées d’une rotation et d’une homothétie de même centre;
- du point de vue numérique, ce sont exactement les fonctions du type $f:z\mapsto az+b$ où $a\neq0$ et $b$ sont deux nombres complexes.
Plus précisément, montrons que ces deux ensembles sont les mêmes :
- les translations, rotations et homothéties du plan complexe s’écrivent
- translation : $T_{\vec{U}}:z\mapsto z+u$ où $u$ est l’affixe du vecteur $\vec{U}$;
- rotation : $R_{C,\theta}:z\mapsto e^{i\theta}(z-c)+c$ où $c$ est l’affixe du point $C$, centre de la rotation;
- homothétie : $H_{C,r}:z\mapsto r(z-c)+c$ où $r>0$ est le rapport d’homothétie et $c$ l’affixe de son centre $C$.
Dire que ces transformations ou leur composées s’écrivent sous la forme $f:z\mapsto az+b$ revient donc simplement à développer et simplifier les produits et sommes entrant en jeu dans leur définition.
- Réciproquement, soit $f:z\mapsto az+b$.
Si $a=1$, alors il s’agit d’une translation.
Sinon, son centre est obtenu comme l’unique point fixe de la transformation. Autrement dit, il suffit de résoudre l’équation \(f(c)=c\Leftrightarrow c=\dfrac{b}{1-a}\) pour obtenir son affixe.
Ceci étant fait, il suffit alors de remarquer que \(f(z)=az+\dfrac{b(1-a)}{1-a}=a(z-c)+c\) et d’écrire $a=re^{i\theta}$ pour montrer que cette transformation est bien la composée de la rotation de centre $c$ et d’angle $\theta$ et de l’homothétie de même centre et rapport $r$.
De l’utilité des isométries dans l’étude des transformations complexes
Considérons maintenant une fonction $f:\mathbf{C}\rightarrow\mathbf{C}$, dérivable en un sens que je ne précise pas - voir l’article sur les fonctions holomorphes pour plus de détail.
En utilisant la formule de Taylor, on a alors $f(z)=f(z_0)+f’(z_0)\left(z-z_0\right)+\underset{z_0}{o}\left(z-z_0\right)$.
Autrement dit, en posant $a=f’(z_0)$ et $b=f(z_0)-z_0f’(z_0)$, localement, si $f’(z_0)\neq0$, cette application se comporte comme la similitude directe $z\mapsto az+b$ : donc elle conserve, localement, les angles orientés.
Les fonctions dérivables de la variable complexe sont donc, en tout point où leur dérivée ne s’annule pas, des transformations conformes. Cela a notamment pour conséquence que ces fonctions envoient un réseau de droites orthogonales sur un réseau de courbes orthogonales.
Exemple de la fonction exponentielle
La fonction $\exp$ est dérivable, de dérivée $\exp’=\exp$. De plus sa dérivée ne s’annule jamais ! Elle est donc conforme en tout point.
En revanche, vue comme une fonction de $\mathbf{C}$ dans $\mathbf{C}$, elle n’est pas bijective : ce n’est pas une transformation du plan complexe dans son ensemble.
Plus précisément :
- $e^{z+2ik\pi}=e^z$ pour tout entier $k$, il faut donc restreindre l’ensemble de départ à une bande comprenant des points du plan complexe dont la partie imaginaire se trouve dans un intervalle d’amplitude $2\pi$. Par exemple,
\(B=\{x+iy, x\in\mathbf{R},y\in]-\pi;\pi]\}\) - l’équation $e^z=c$ admet des solutions pour tout complexe $c\neq0$. Il faut donc restreindre l’ensemble d’arrivée aux complexes non nuls, $\mathbf{C}^*$.
$\exp : B\rightarrow\mathbf{C}^*$ est une transformation conforme de la bande $B$ sur l’ensemble des nombres complexes non nuls ! Pour comprendre comment on peut envoyer une bande horizontale infinie sur l’ensemble du plan complexe sauf un point… le mieux est de faire des dessins !
Représentations graphiques
Le principe des représentations graphiques de fonctions de $\mathcal{U}\subset\mathbf{C}$ dans $\mathcal{V}\subset\mathbf{C}$ est de recouvrir l’espace de départ d’un motif puis d’observer sa déformation dans l’espace d’arrivée après transformation.
Partons d’un exemple où le motif est constitué de droites verticales et horizontales :
import confmap as cm
import numpy as np
motif = 255*np.ones((200,200,3),dtype=np.uint8)
motif[:,:10,1:]=0
motif[:,50:60,1:]=0
motif[:,100:110,1:]=0
motif[:,150:160,1:]=0
motif[95:105,:,:2]=0
im = cm.ImageTransform('./exp.jpg',1,'./Exports/',600,600,c=1,d=0,
data=motif)
im.transform()
Voici le motif dans l’espace de départ :

$0$ est au centre de l’image, le coin supérieur droit a pour affixe $1+i$ et le coin inférieur gauche $-1-i$.
On effectue alors l’image de ce motif par la fonction exponentielle (en effectuant une homothétie de rapport $c=\pi$ d’abord - voir paramètre $c$ de la fonction $\exp$):
import confmap as cm
import numpy as np
motif = 255*np.ones((200,200,3),dtype=np.uint8)
motif[:,:10,1:]=0
motif[:,50:60,1:]=0
motif[:,100:110,1:]=0
motif[:,150:160,1:]=0
motif[95:105,:,:2]=0
im = cm.ImageTransform('./exp.jpg',2,'./Exports/',600,600,c=1,d=0,
data=motif)
im.exp(auto=False,angle=False,c=np.pi)
im.transform()
Image du motif dans l’espace d’arrivée :
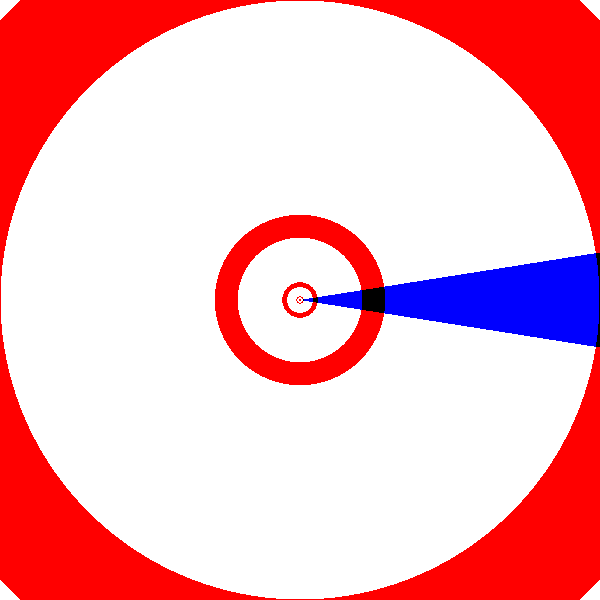
Ce qui permet de voir finalement la fonction $\exp$ comme la transformation suivante :
 $\overset{\exp}{\longrightarrow}$
$\overset{\exp}{\longrightarrow}$
En changeant légèrement le motif :
motif = 255*np.ones((200,200,3),dtype=np.uint8)
motif[:,:10,1:]=0
motif[:,50:60,1:]=0
motif[:,100:110,1:]=0
motif[:,150:160,1:]=0
motif[95:105,:,:2]=0
motif[195:,:,[0,2]]=motif[:5,:,[0,2]]=0
im = ...
 $\overset{\exp}{\longrightarrow}$
$\overset{\exp}{\longrightarrow}$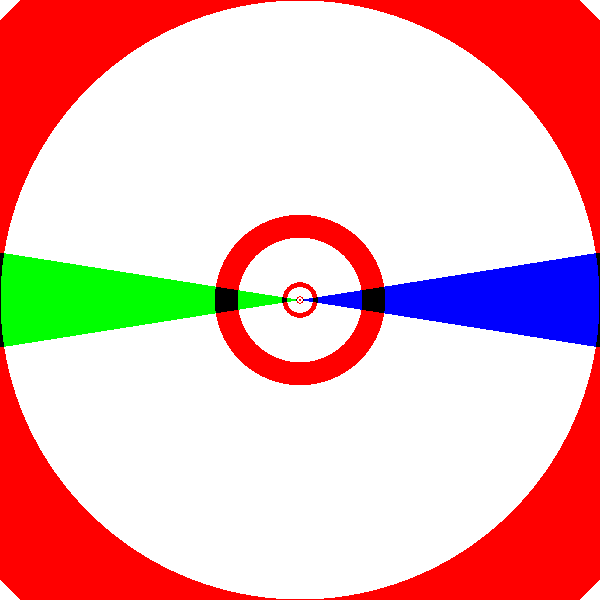
Amusons nous un peu : opérons une similitude (pas n’importe laquelle !) avant l’image par $\exp$
...
im = cm.ImageTransform('./exp.jpg',6,'./Exports/',600,600,c=1,d=0,
data=motif)
im.similitude(c=np.exp(1j*np.pi/4)/2**0.5)
im.exp(auto=False,angle=False,c=np.pi)
im.transform()
 $\overset{\exp}{\longrightarrow}$
$\overset{\exp}{\longrightarrow}$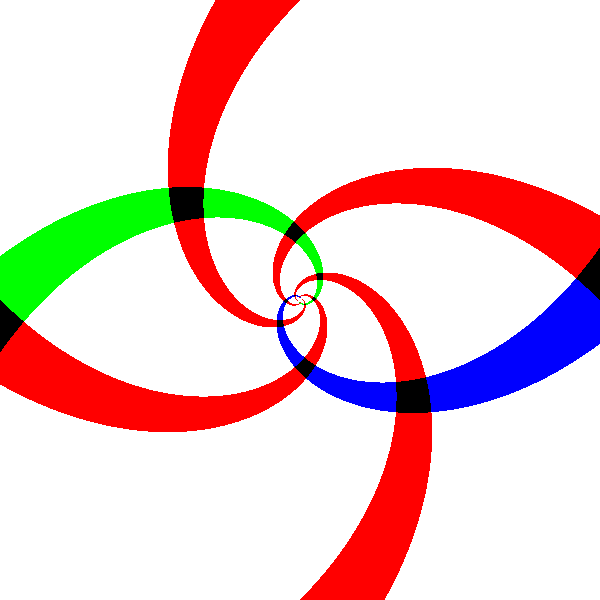
Et une autre similitude (toujours pas n’importe laquelle !) :
...
im.similitude(c=np.exp(1j*np.arctan(2))/5**0.5)
...
 $\overset{\exp}{\longrightarrow}$
$\overset{\exp}{\longrightarrow}$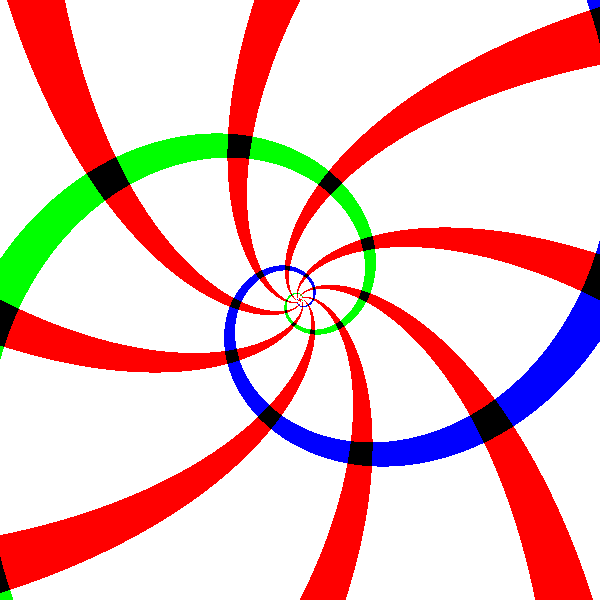
ConfMap est conçu pour faire automatiquement ces similitudes particulières…
...
im = cm.ImageTransform('./exp.jpg',10,'./Exports/',600,600,c=1,d=0,
data=motif)
im.exp(N=5,P=3)
im.transform()

… et pour pouvoir remplacer le motif par n’importe quelle image !
import confmap as cm
im = cm.ImageTransform('./MONIMAGE.jpg',10,'./Exports/',1600,900,c=1,d=0.5j)
im.mirror()
im.exp(N=1,P=1)
im.transform()
Bonus : Bernhard Riemann fut le premier à s’intéresser à cette interprétation géométrique des fonctions complexes d’une variable complexe. En hommage, une vidéo permettant de visualiser la transformation : on déforme progressivement l’espace de départ pour arriver à son image par la fonction $\exp$.
