Cet article fait suite à mon troisième article où je donnais les fondements mathématiques d’un algorithme d’interpolation des données officielles publiées pour l’épidémie de CoViD19.

Les explications que j’y donnais étaient entachées d’une erreur de calcul… qui s’avère miraculeuse ! J’explique ici pourquoi.

Rappels et notations

Je reprends, sans les expliquer, les résultats et notations introduits dans mon précédent article.

On souhaite approximer un nuage de points par une sigmoïde : nous noterons $f(a,b,c):x\in\mathbb{R}\mapsto\dfrac{c}{1+e^{-(ax+b)}}=\dfrac{c}{1+e^{-a(x-t_0)}}$ les fonctions que nous souhaitons utiliser pour cette approximation.

Le nuage de points est donné par la liste $\left((X_i;Y_i)\right)_{1\leq i\leq n}$ de ses coordonnées.

On souhaite minimiser la quantité $S(a,b,c)=\displaystyle\sum_{i=1}^n\left[f(a,b,c)(X_i)-Y_i\right]^2$

On note $F_c:u\mapsto\dfrac{c}{1+e^{-u}}$ et $G_c:u\mapsto\ln\left(\dfrac{u}{c-u}\right)$ et $L_i=G_c(Y_i)$. Je donnais les équations suivantes pour fondement théorique de mon algorithme :

\[(E_1):~~c=\dfrac{\displaystyle\sum_i\frac{Y_i}{1+\exp\left(-(aX_i+b)\right)}}{\displaystyle\sum_i\frac{1}{\left(1+\exp\left(-(aX_i+b)\right)\right)^2}}\] \[S(a,b,c)=\displaystyle\sum_{i=1}^n\left[f(a,b,c)(X_i)-Y_i\right]^2=\sum_{i=1}^n\left[F_c(aX_i+b)-F_c(L_i)\right]^2\]

En utilisant le développement limité de $F_c$ au voisinage de $L_i$ on obtient une expression approximative de $S$ : $S(a,b,c)\approx\displaystyle\sum_{i=1}^n\left[F_c'(L_i)\left(aX_i+b-L_i\right)\right]^2$

\[(E_e):~~S(a,b,c)\approx\sum_i\left(aX_i+b-L_i\right)^2aY_i^2\left(1-\frac{Y_i}{c}\right)^2\]

Puis,

\[P_i=L_i^2\left(1-\frac{L_i}{c}\right)^2{~~;~~}\overline{L}=\dfrac{\displaystyle\sum_iP_iL_i}{\displaystyle\sum_iP_i}{~~;~~}\overline{X}=\dfrac{\displaystyle\sum_iP_iX_i}{\displaystyle\sum_iP_i}\] \[\overline{A}=\displaystyle\sum_iP_i\left(X_i-\overline{X}\right)\left(2X_i-\overline{X}\right){~~;~~}\overline{B}=\displaystyle\sum_iP_i\left(3X_i-2\overline{X}\right)\left(\overline{L}-L_i\right)\] \[\overline{C}=\displaystyle\sum_iP_i\left(\overline{L}-L_i\right)^2{~~;~~}\overline{\Delta}=\overline{B}^2-4\overline{A}\overline{C}\]

Enfin

\[(E_2):~~a=\dfrac{-\overline{B}+\sqrt{\overline{\Delta}}}{2\overline{A}}\] \[(E_3):~~b=\overline{L}-a\overline{X}\]

J’appellerai méthode 1 la méthode fondée sur ces résultats fautifs.

L’erreur de calcul

L’équation $(E_e)$ est fautive : la bonne équation est la suivante

\[(E_b):~~S(a,b,c)\approx\sum_i\left(aX_i+b-L_i\right)^2Y_i^2\left(1-\frac{Y_i}{c}\right)^2\]

Elle donne la valeur de $a$ suivante (celle de $b$ restant inchangée) :

\[(E_2'):~~a=\dfrac{\displaystyle\sum_iP_i\left(L_i-\overline{L}\right)\left(X_i-\overline{X}\right)}{\displaystyle\sum_iP_i\left(X_i-\overline{X}\right)^2}\]

J’appellerai méthode 0 la méthode fondée sur le remplacement de l’équation $(E_2)$ par l’équation $(E_2’)$.

Une troisième méthode

La simplification des calculs permise par le remplacement de $(E_2)$ par $(E_2’)$ autorise à faire un développement limité d’ordre supérieur dans $(E_b)$. On obtient alors l’équation

\[(E_b'):~~S(a,b,c)\approx\sum_i\left(aX_i+b-L_i\right)^2P_i\left[1+\left(aX_i+b-L_i\right)\left(1-2Y_i/c\right)\right]\]

Je passe le reste des calculs, mais l’utilisation de cette nouvelle approximation de $S$ conduit à une troisième méthode que j’appellerai méthode 2.

Discussion : l’erreur miraculeuse

Il est étonnant au premier abord que l’erreur que j’ai commise ait conduit à la méthode 1 qui s’avère non seulement précise mais surtout plus stable que les deux autres. La raison - que j’ai eu un peu de mal à comprendre - en est la suivante : on cherche à minimiser $a\mapsto S(a)$ qui est une fonction positive (et même selon toutes probabilités, strictement positive) passant par un minimum pour une valeur de $a$ positive (au moins pour les données qu’on cherche à interpoler ici).

L’erreur que j’ai commise revient à minimiser $a\mapsto aS(a)$ en cherchant une valeur du paramètre $a$ strictement positif pour laquelle cette fonction passe par un minimum local. Ceci a pour effet de sous-évaluer la valeur optimale du paramètre $a$ et de stabiliser l’algorithme (pour des raisons que je ne développe pas).

Je me retrouve ainsi avec trois méthodes :

La méthode 1 a tendance à minorer les données qu’on lui fournit. Elle est cependant extrêmement stable et conduit, au moins pour tous les jeux de données que j’ai utilisés jusque-là, à une convergence systématique des paramètres.
La méthode 0 a tendance à minorer les données qu’on lui fournit. Elle ne conduit pas toujours à une convergence des paramètres. Lorsqu’elle diverge, je la remplace par la méthode 1.
La méthode 2 est bien plus affinée que les précédentes, notamment elle anticipe beaucoup mieux le nombre asymptotique de cas atteints. Cependant, elle ne conduit pas toujours à une convergence des paramètres. Lorsqu’elle diverge, je la remplace par la méthode 1.

Les méthodes 0 et 2 remplacent ainsi avantageusement les évaluations optimistes et pessimistes que je faisais jusque-là. Notamment, la méthode 2 se révèle extrêmement clairvoyante sur l’anticipation de la gravité de l’épidémie.

Algorithme

"""
Created on Fri Apr 04 06:17:53 2020

@author: François Coulombeau
"""

import numpy as np
import matplotlib.pyplot as plt
import datetime as dtm
import matplotlib.dates as mdates
import matplotlib.patches as mpat
import os

np.seterr(all='raise')

Param_a = 0
Param_b = 1
Param_c = 2

Taux = 3
Inflexion = 4

Prev_vs_Real = 5
Fit = 6
Pic = 7

def reglin(X,L,Y,c,method=1):
    """Calcul des coefficients de la droite de régression Y = a*X+b où chaque 
    point (x_i,y_i) est pondéré par le poids donné dans la liste optionnelle."""
    P = np.array((Y*(1-Y/c))**2,dtype=np.float64)
    N = np.sum(P)
    P = P/N
    moyX = sum(P*X)
    moyL = sum(P*L)
    if method==0 :
        B = sum(P*(X*L-moyX*moyL))
        C = sum(P*(X**2-moyX**2))
        a = B/C
        b = moyL-a*moyX
    elif method==1:
        A = sum(P*2*(X**2-moyX**2))
        B = sum(P*3*(moyX*moyL-L*X))
        C = sum(P*(L**2-moyL**2))
        Delta = B**2-4*A*C
        try:
            a = (-B+Delta**0.5)/A/2
            b = moyL-a*moyX
        except FloatingPointError:
            A = sum(P*3*(X-moyX)**3*(1-2*Y/c))
            B = sum(P*2*(X-moyX)**2*(1-3*(L-moyL)*(1-2*Y/c)))
            C = sum(P*(X-moyX)*(L-moyL)*(3*(L-moyL)*(1-2*Y/c)-2))
            Delta = B**2-4*A*C
            a = (-B+Delta**0.5)/A/2
            A = sum(3*P*(1-2*Y/c))
            B = sum(2*P*(1+3*(a*X-L)*(1-2*Y/c)))
            C = sum(P*(a*X-L)*(2+3*(a*X-L)*(1-2*Y/c)))
            Delta = B**2-4*A*C
            b = (-B+Delta**0.5)/A/2
    elif method==2:
        A = sum(P*3*(X-moyX)**3*(1-2*Y/c))
        B = sum(P*2*(X-moyX)**2*(1-3*(L-moyL)*(1-2*Y/c)))
        C = sum(P*(X-moyX)*(L-moyL)*(3*(L-moyL)*(1-2*Y/c)-2))
        Delta = B**2-4*A*C
        try:
            a = (-B+Delta**0.5)/A/2
            A = sum(3*P*(1-2*Y/c))
            B = sum(2*P*(1+3*(a*X-L)*(1-2*Y/c)))
            C = sum(P*(a*X-L)*(2+3*(a*X-L)*(1-2*Y/c)))
            Delta = B**2-4*A*C
            b = (-B+Delta**0.5)/A/2
        except FloatingPointError:
            A = sum(P*2*(X**2-moyX**2))
            B = sum(P*3*(moyX*moyL-L*X))
            C = sum(P*(L**2-moyL**2))
            Delta = B**2-4*A*C
            a = (-B+Delta**0.5)/A/2
            b = moyL-a*moyX
    return a,b
def f(a,b,c):
    """Renvoie la fonction sigmoïde correspondante."""
    return lambda x:c/(1+np.exp(-(a*x+b)))

def interpSigm(data, fin, S0=0, mxc = 0,mxS=1e6, prec=1e-3):
    """Calcule les paramètres (a,b,c) méthode 1
    méthode 0 : (am,bm,cm)
    méthode 2 : (aM,bM,cM)"""
    n = len(data)
    somcum = [S0+sum(data[:(k+1)]) for k in range(n)]
    somcum = np.array(somcum[:fin],dtype=np.float64)
    X = np.array(range(fin),dtype=np.float64)
    c = cm = cM = max(somcum)*2
    cn = cmn = cMn = 2*c
    m0,m1,m2 = 0,1,2
    i=0
    while (abs(c-cn)>prec*c) or (abs(cm-cmn)>prec*cm) or (abs(cM-cMn)>prec*cM)\
           or (i<=2):
        i+=1
        Y0 = np.log(somcum/(c-somcum))
        a,b = reglin(X,Y0,somcum,c,method=m1)
        Y0 = np.log(somcum/(cm-somcum))
        am,bm = reglin(X,Y0,somcum,cm,method=m0)
        Y0 = np.log(somcum/(cM-somcum))
        aM,bM = reglin(X,Y0,somcum,cM,method=m2)
        cn = c
        cmn = cm
        cMn = cM
        c = np.sum(somcum*f(a,b,1)(X))/np.sum(f(a,b,1)(X)**2)
        cm = np.sum(somcum*f(am,bm,1)(X))/np.sum(f(am,bm,1)(X)**2)
        cM = np.sum(somcum*f(aM,bM,1)(X))/np.sum(f(aM,bM,1)(X)**2)
        if cm>mxS or np.isnan(cm):
            cm=c
            m0=1
        if cM>mxS or np.isnan(cM):
            cM=c
            m2=1
    if mxc>cM:
        cM = mxc*0.+cM*1
        Y0 = np.log(somcum/(cM-somcum))
        aM,bM = reglin(X,Y0,somcum,cM,method=m2)
    return ((am,bm,cm),(a,b,c),(aM,bM,cM))

def caracteristiques(a,b,c,d):
    """Calcule trois paramètres caractéristiques 
    - taux de croissance instantané
    - taux de croissance en -infini
    - jour d'inflexion
    à partir des valeurs de (a,b,c)
    et de celle du jour d pour lequel on cherche la croissance instantanée."""
    taux = a*np.exp(-(a*d+b))/(1+np.exp(-(a*d+b)))
    tauxInit = np.exp(a)-1
    inflexion = -b/a
    return taux,tauxInit,inflexion

def plt_set_fullscreen():
    backend = str(plt.get_backend())
    mgr = plt.get_current_fig_manager()
    if backend == 'TkAgg':
        if os.name == 'nt':
            mgr.window.state('zoomed')
        else:
            mgr.resize(*mgr.window.maxsize())
    elif backend == 'wxAgg':
        mgr.frame.Maximize(True)
    elif backend[:2] == 'Qt':
        mgr.window.showMaximized()

def figDate(both=False,logscale=False, sbp = None, intervalle=1):
    # Nouvelle figure et paramétrage
    if sbp == None:
        plt.figure()
    else:
        plt.subplot(sbp)
    ax = plt.gca()
    formatter = mdates.DateFormatter("%d/%m")
    ax.xaxis.set_major_formatter(formatter)
    locator = mdates.DayLocator(interval=intervalle)
    ax.xaxis.set_major_locator(locator)
    if both:
        ax.yaxis.set_major_formatter(formatter)
        locator = mdates.DayLocator()
        ax.yaxis.set_major_locator(locator)
    if logscale:
        ax.yscale='log'

def evol(dates,listes,titre,typeDonnees, sbp = None, legend=True):
    Lam,La,LaM = listes
    inter = len(dates)//10+1
    figDate(sbp=sbp,intervalle=inter)
    plt.plot(dates,La,'k')
    plt.plot(dates,Lam,'-.k')
    plt.plot(dates,LaM,':k')
    plt.title(titre+"""
        pour les """+typeDonnees)
    plt.xticks(rotation = 45)
    if legend:
        plt.legend([u"Méthode 1",
                u"Méthode 0",
                u"Méthode 2"])

def evol_taux(dates, T1, T2, typeDonnees, sbp = None, legend=True):
    inter = len(dates)//10+1
    figDate(sbp=sbp,intervalle=inter)
    plt.plot(dates,T1)
    plt.plot(dates,T2)
    plt.title(u"""Evolution des taux caractéristiques et instantanés avec le temps
        pour les """+typeDonnees)
    plt.xticks(rotation = 45)
    if legend:
        plt.legend([u"Taux d'évolution instantané",
                u"Taux d'évolution initial"])
    
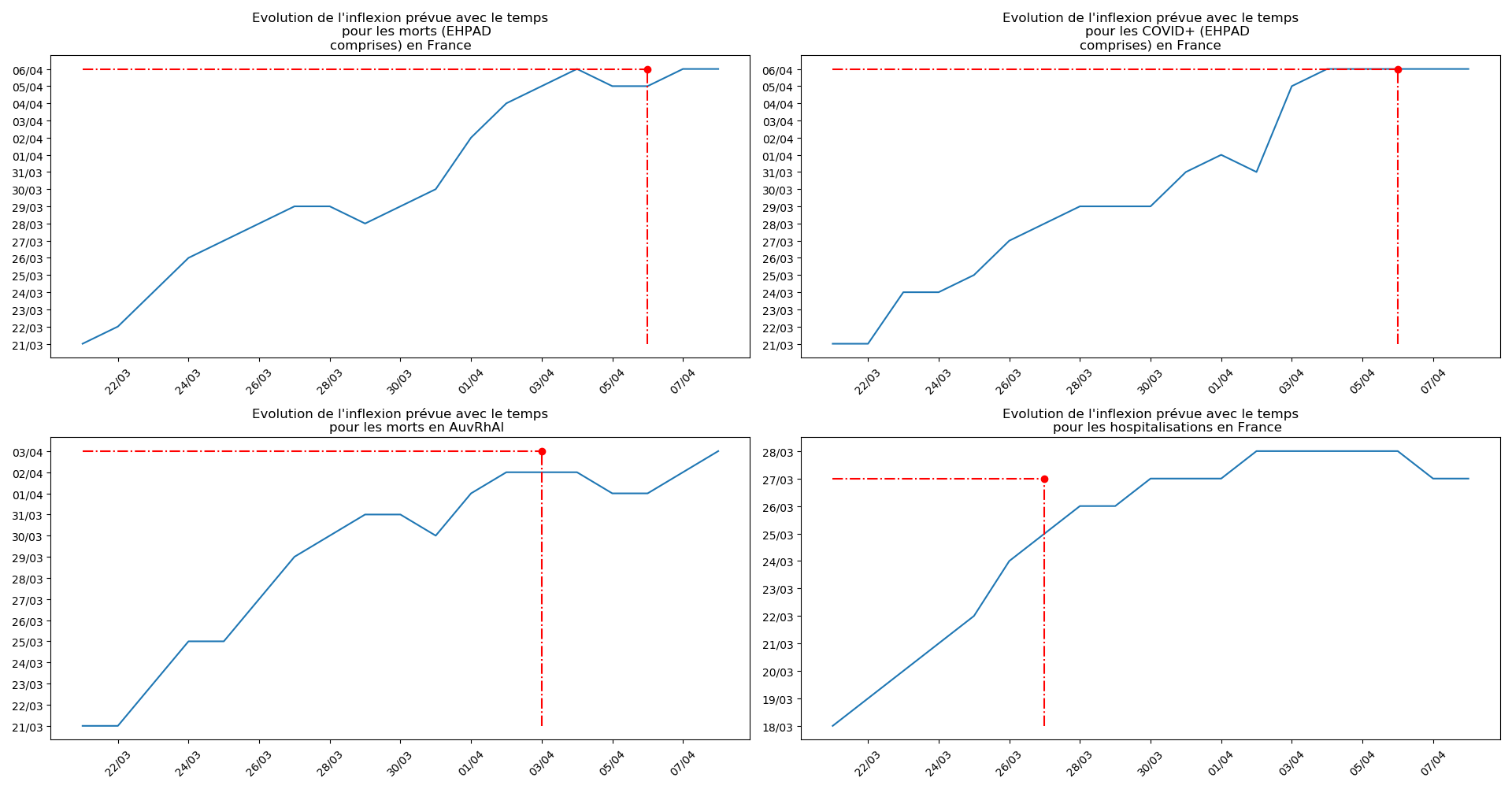
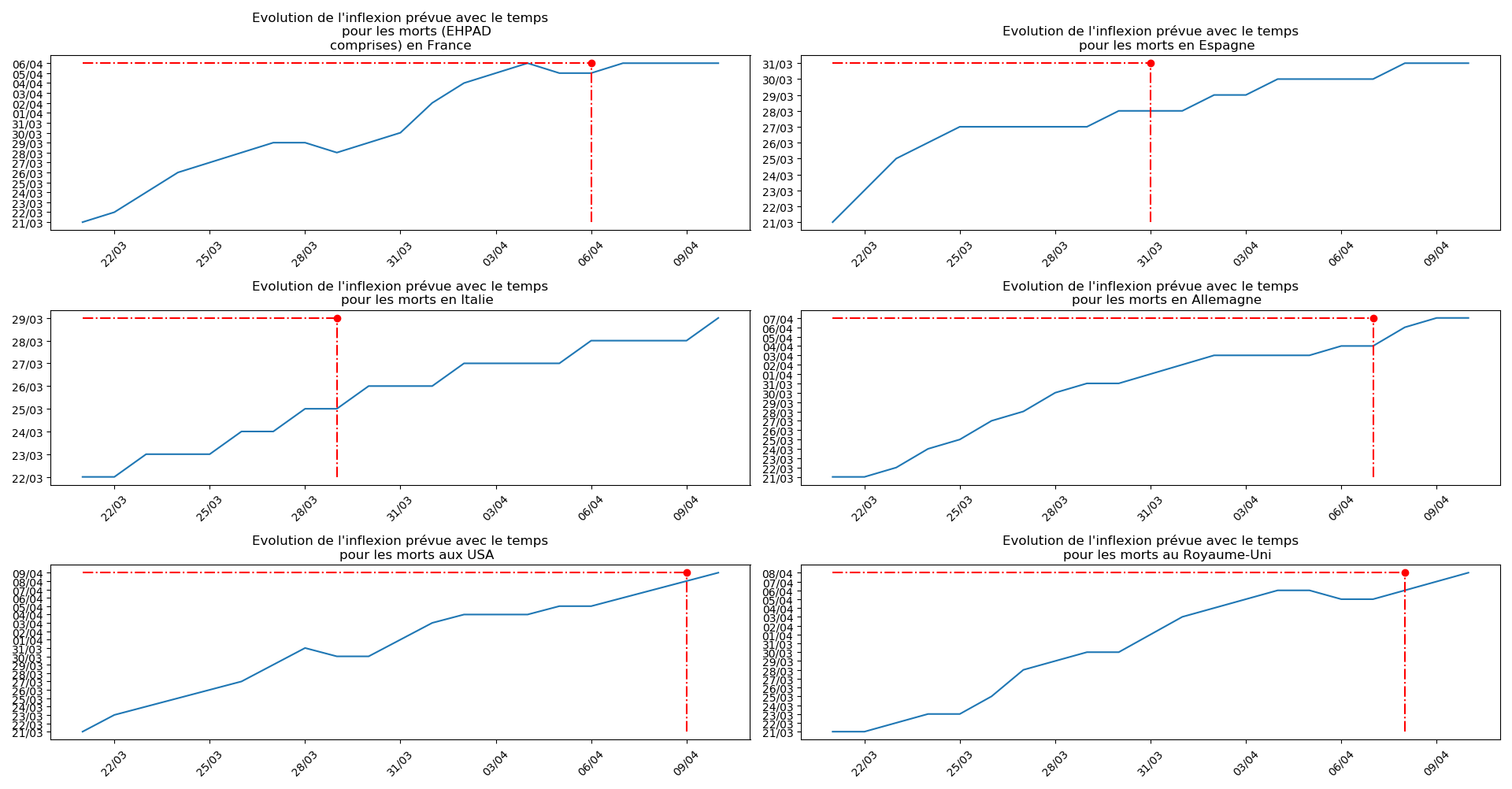
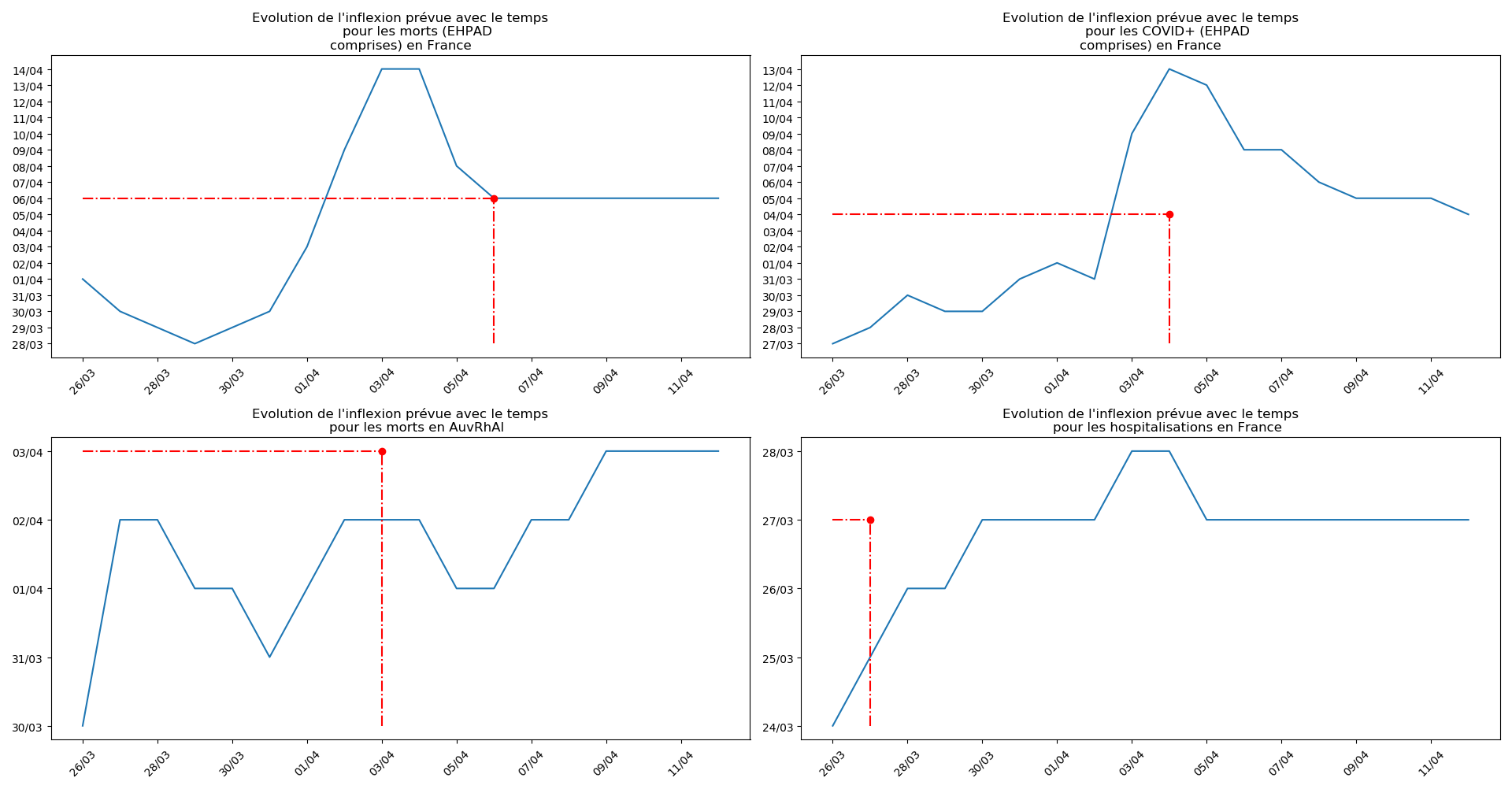
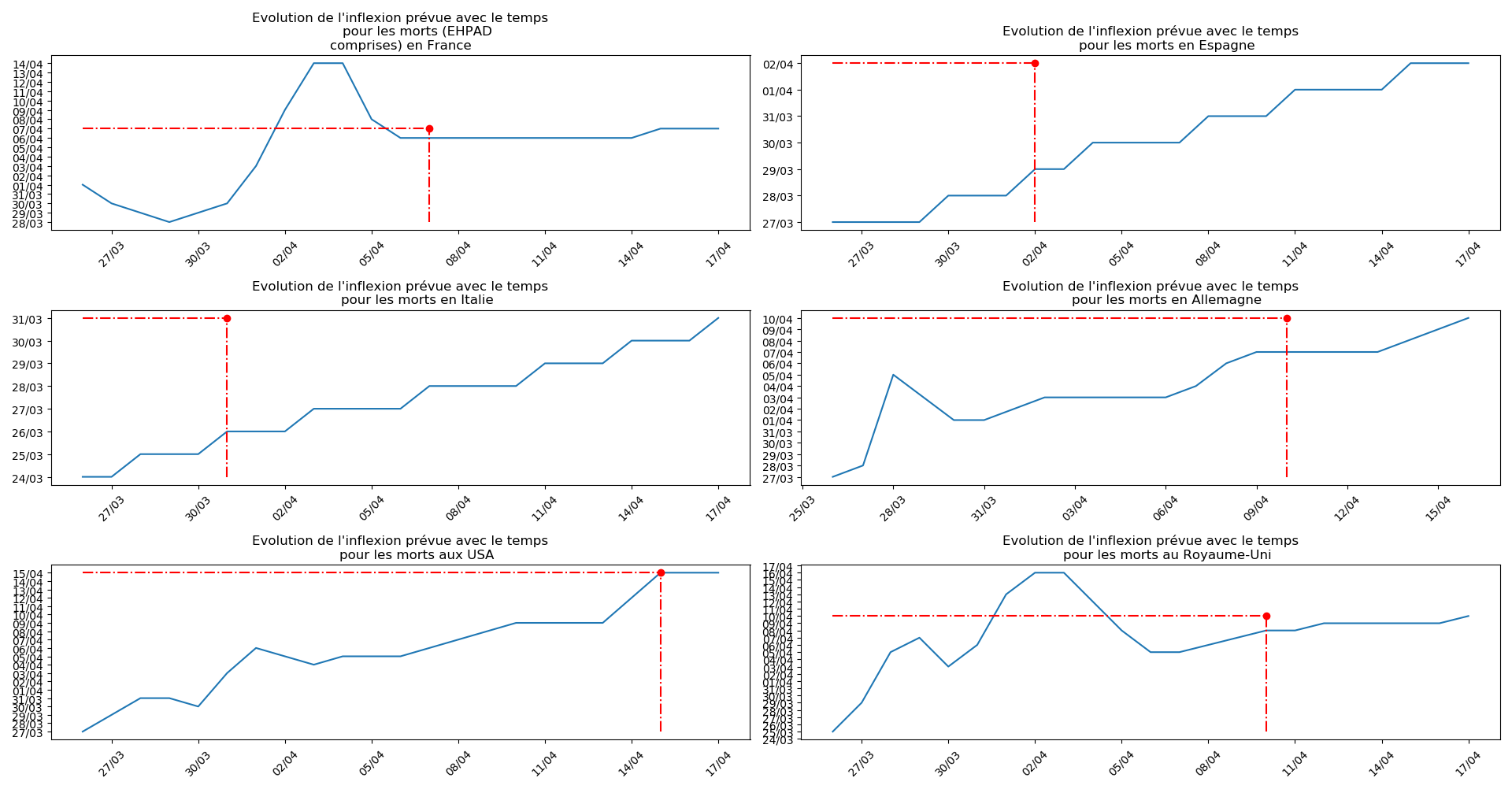
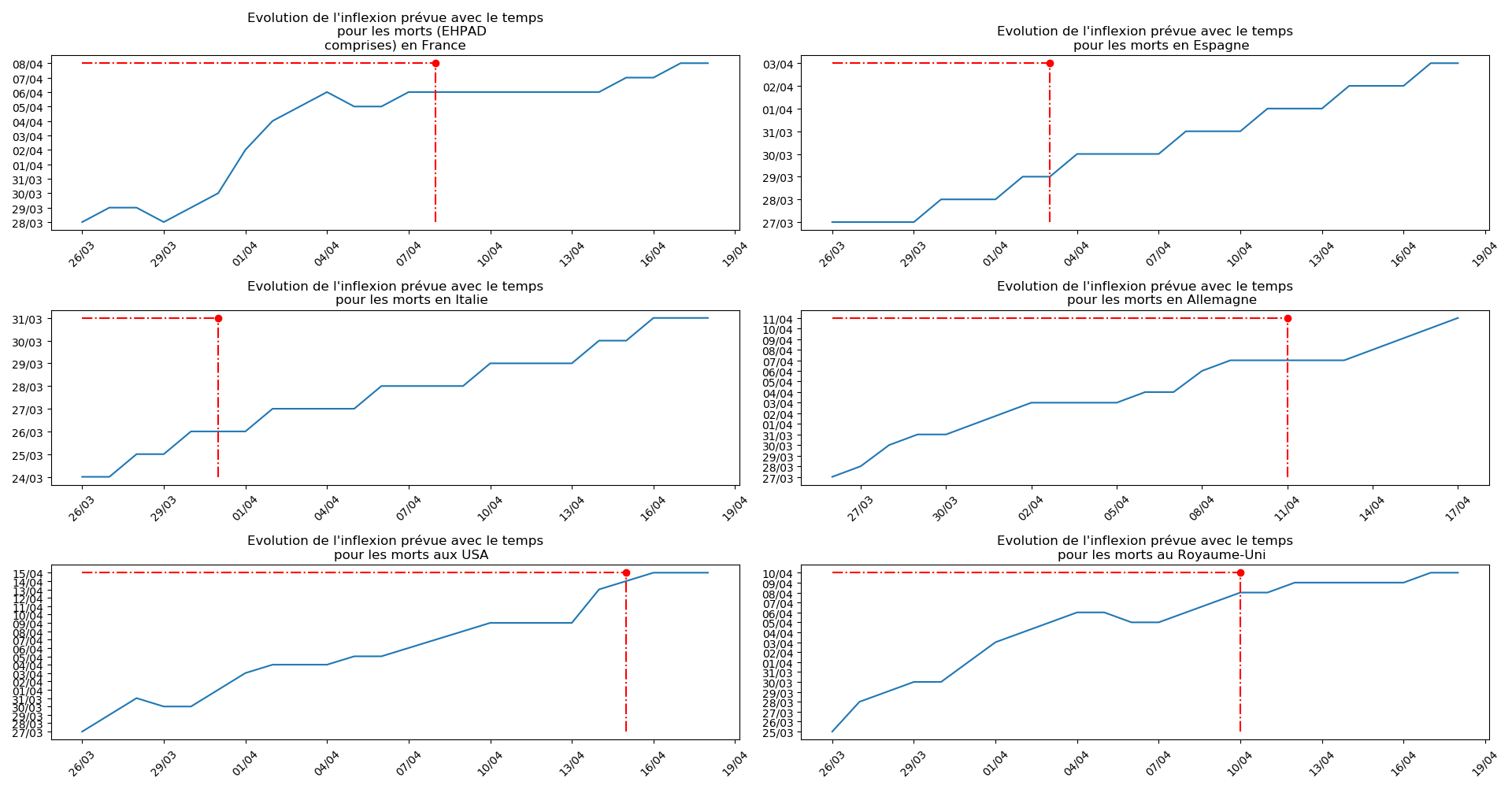
def evol_inflexion(dates, T3, typeDonnees, sbp = None):
    inter = len(dates)//10+1
    figDate(both=True,sbp=sbp,intervalle=inter)
    plt.plot(dates,T3)
    plt.title(u"""Evolution de l'inflexion prévue avec le temps
        pour les """+typeDonnees)
    plt.plot(T3[-1],T3[-1],'or')
    plt.plot([dates[0],T3[-1]],[T3[-1],T3[-1]],'-.r')
    plt.plot([T3[-1],T3[-1]],[np.min(T3),T3[-1]],'-.r')
    plt.xticks(rotation = 45)
    
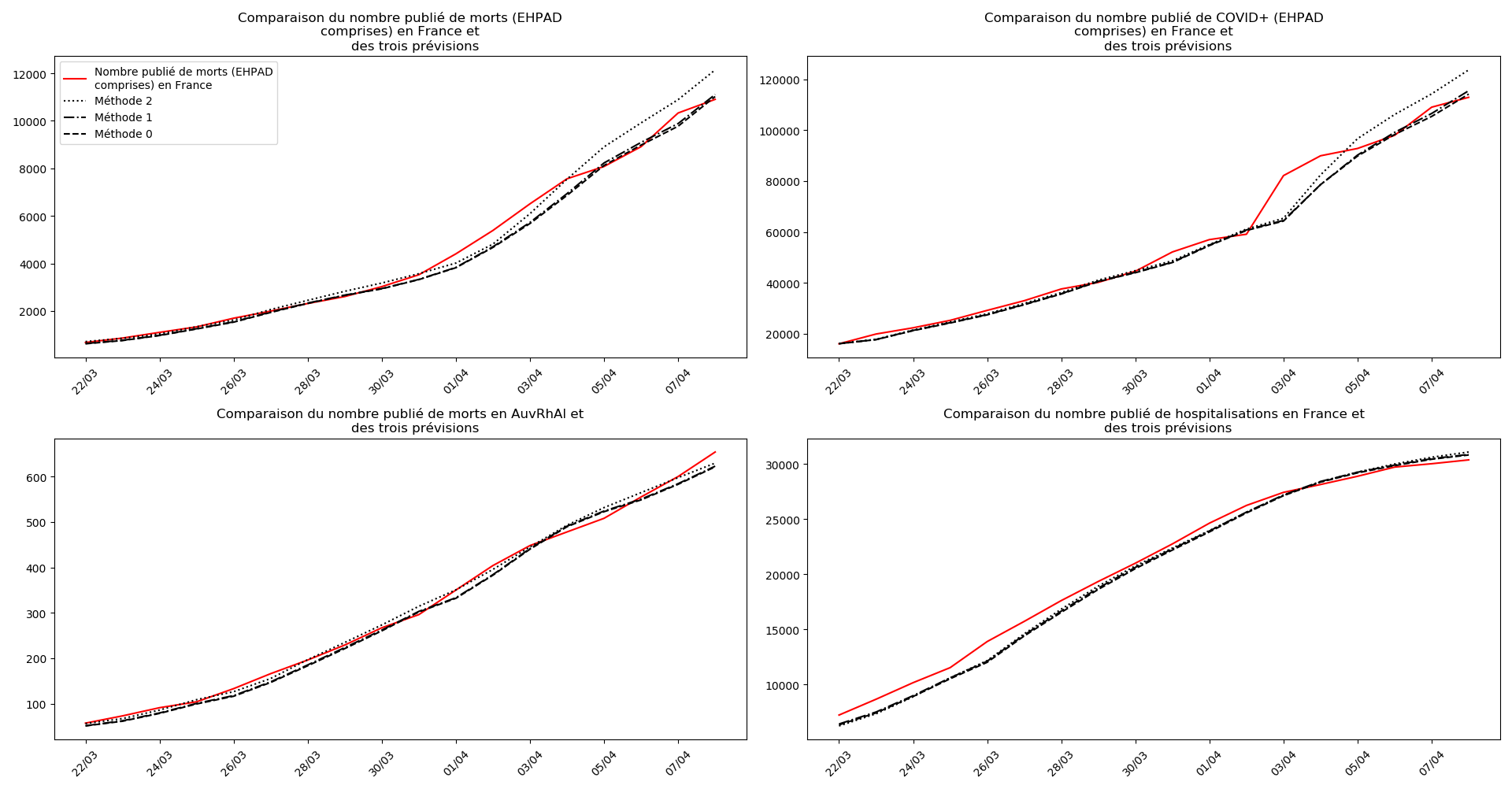
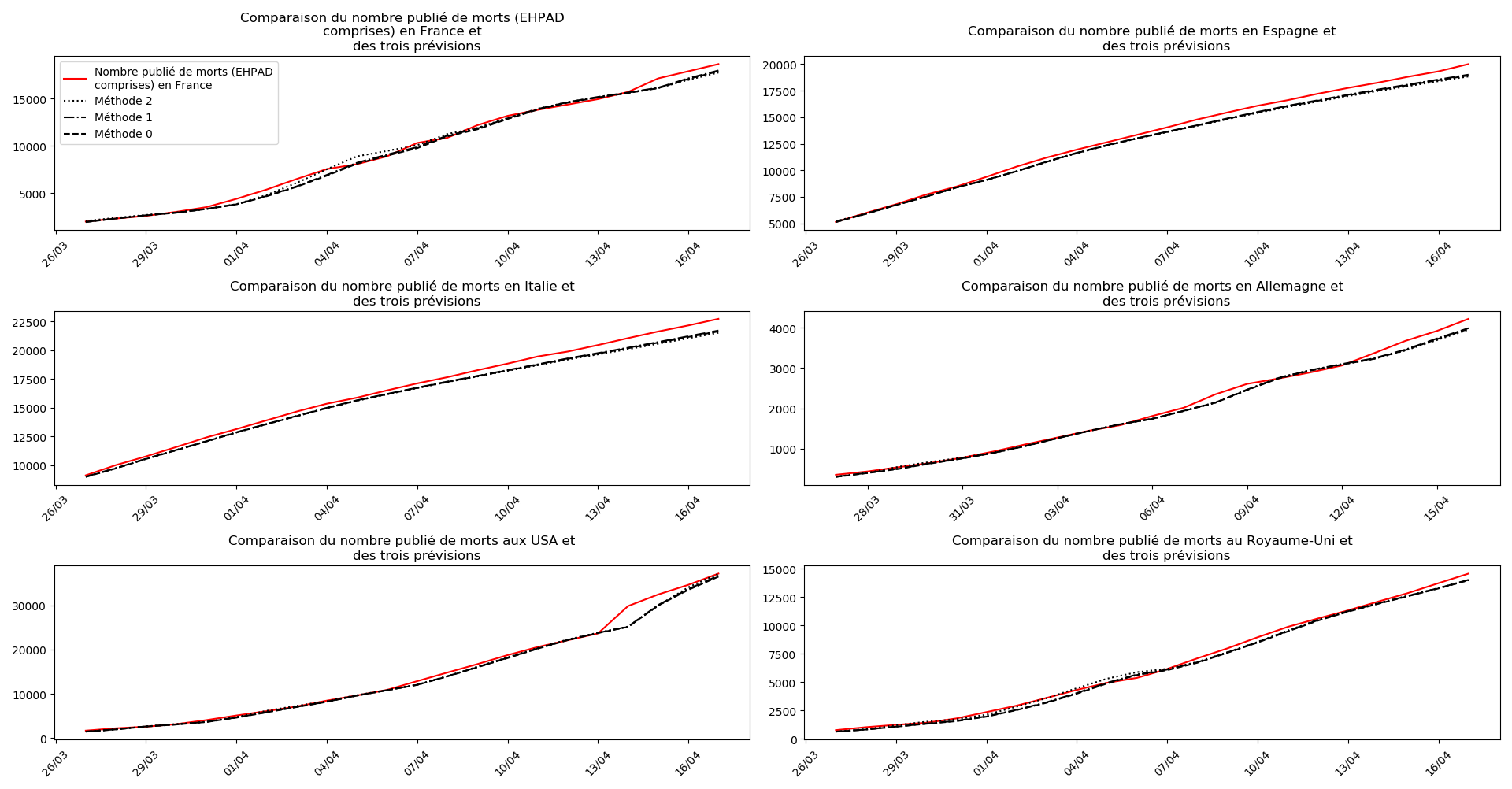
def evol_previsions(dates, listes, nouveaux, somcum, debf, typeDonnees,
                    sbp = None, legend=True):
    n=len(nouveaux)
    Lam,La,LaM,Lbm,Lb,LbM,Lcm,Lc,LcM = listes
    inter = (n-debf)//10+1
    figDate(sbp=sbp,intervalle=inter)
    prev = [f(LaM[i],LbM[i],LcM[i])(debf+i) for i in range(n-debf)]
    plt.plot(dates[1:],somcum[-n+debf:],'r')
    plt.plot(dates[1:],prev,':k')
    prev = [f(La[i],Lb[i],Lc[i])(debf+i) for i in range(n-debf)]
    plt.plot(dates[1:],prev,'-.k')
    prev = [f(Lam[i],Lbm[i],Lcm[i])(debf+i) for i in range(n-debf)]
    plt.plot(dates[1:],prev,'--k')
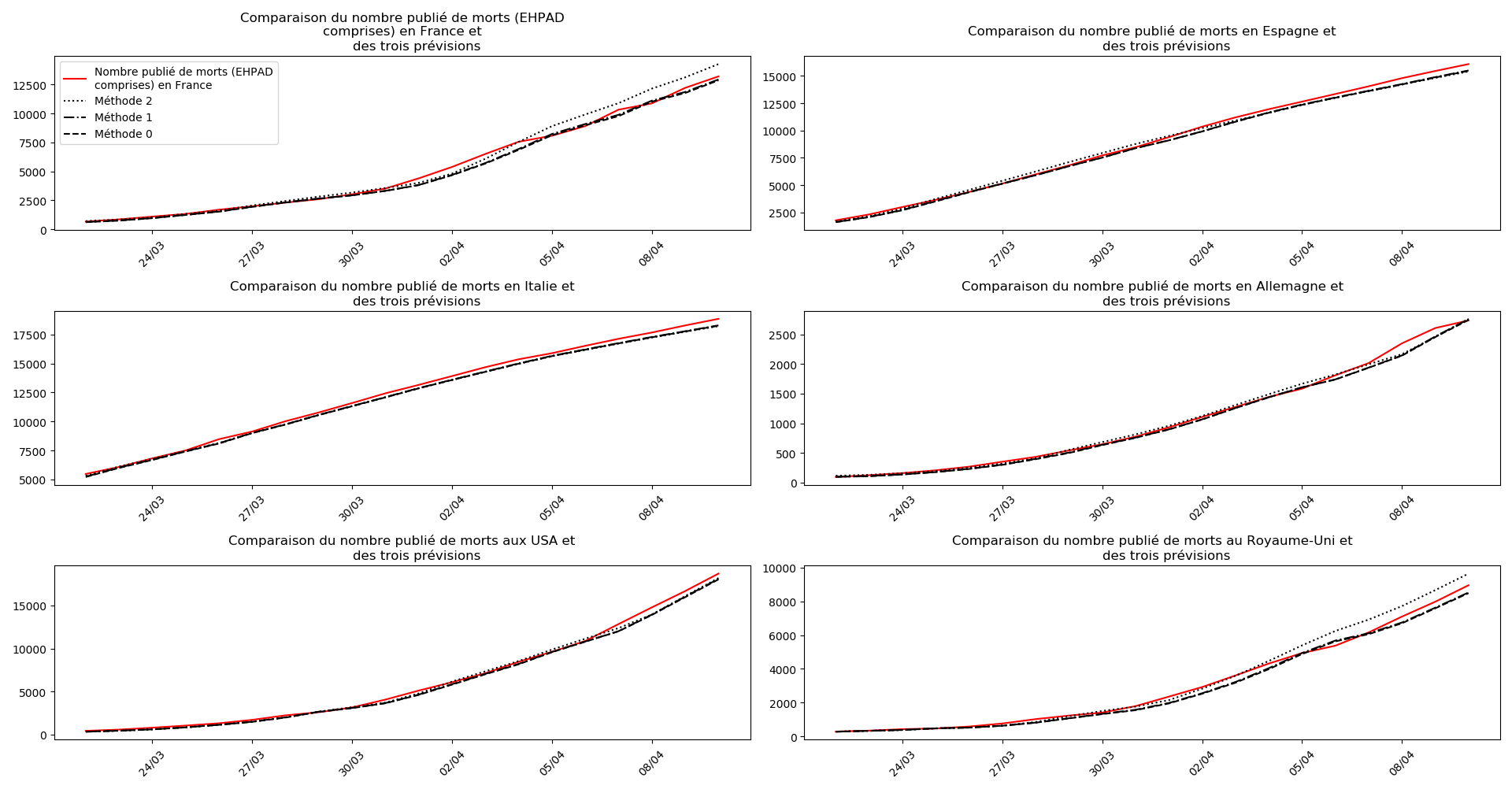
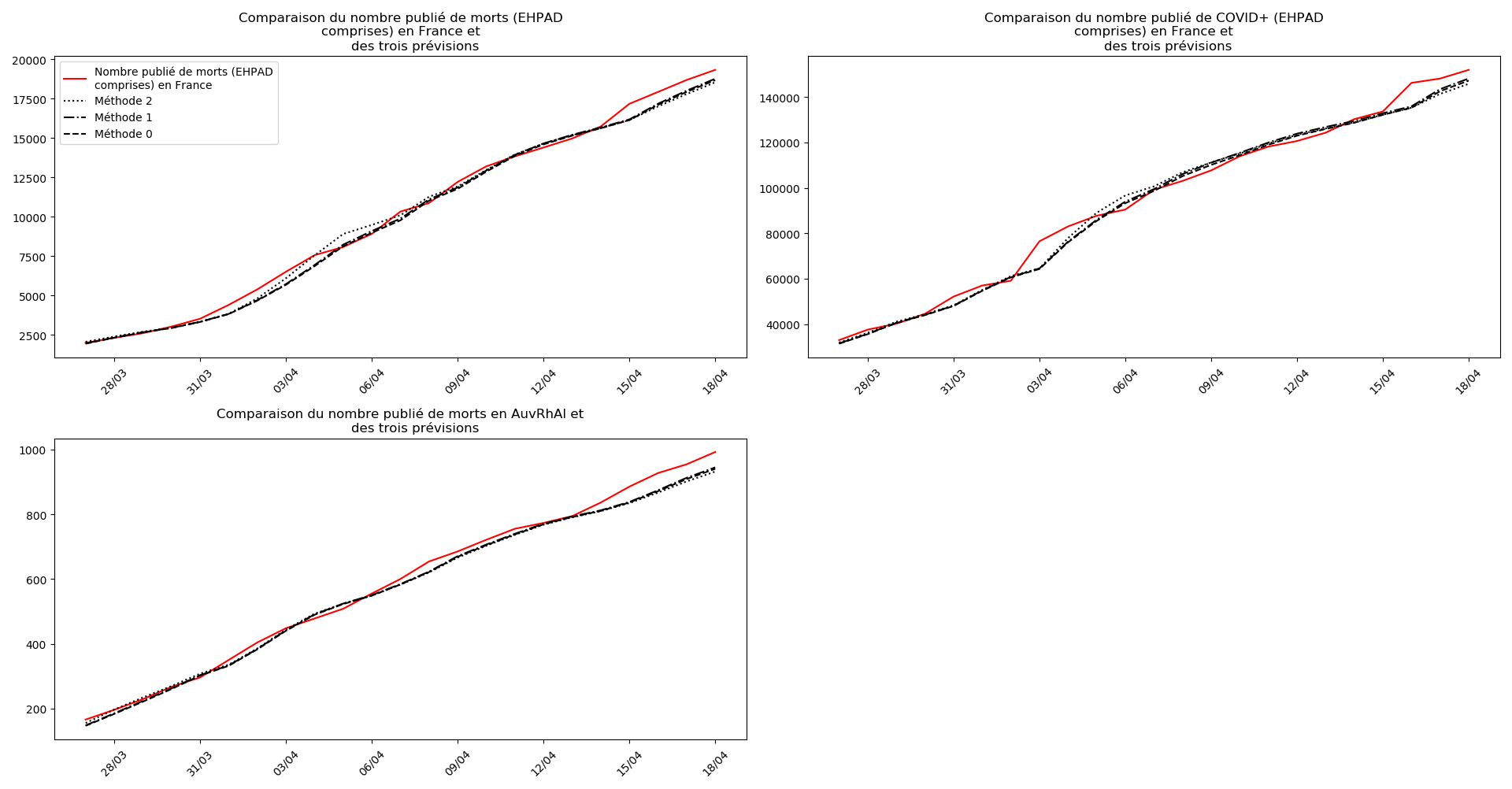
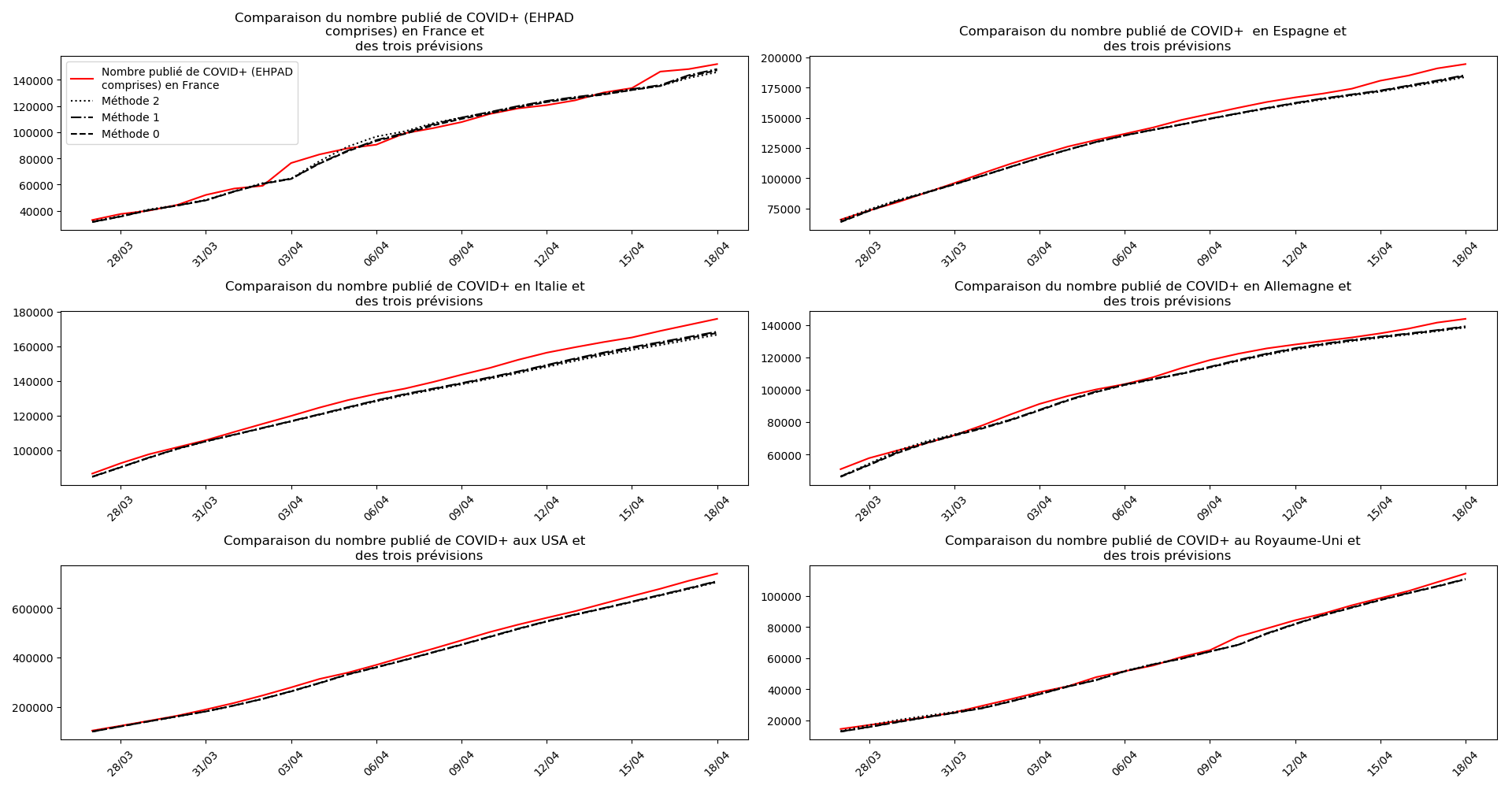
    plt.title(u"""Comparaison du nombre publié de """+typeDonnees+u""" et
        des trois prévisions """)
    plt.xticks(rotation = 45)
    if legend:
        plt.legend([u"Nombre publié de "+typeDonnees,u"Méthode 2",
                u"Méthode 1",
                u"Méthode 0"])
    
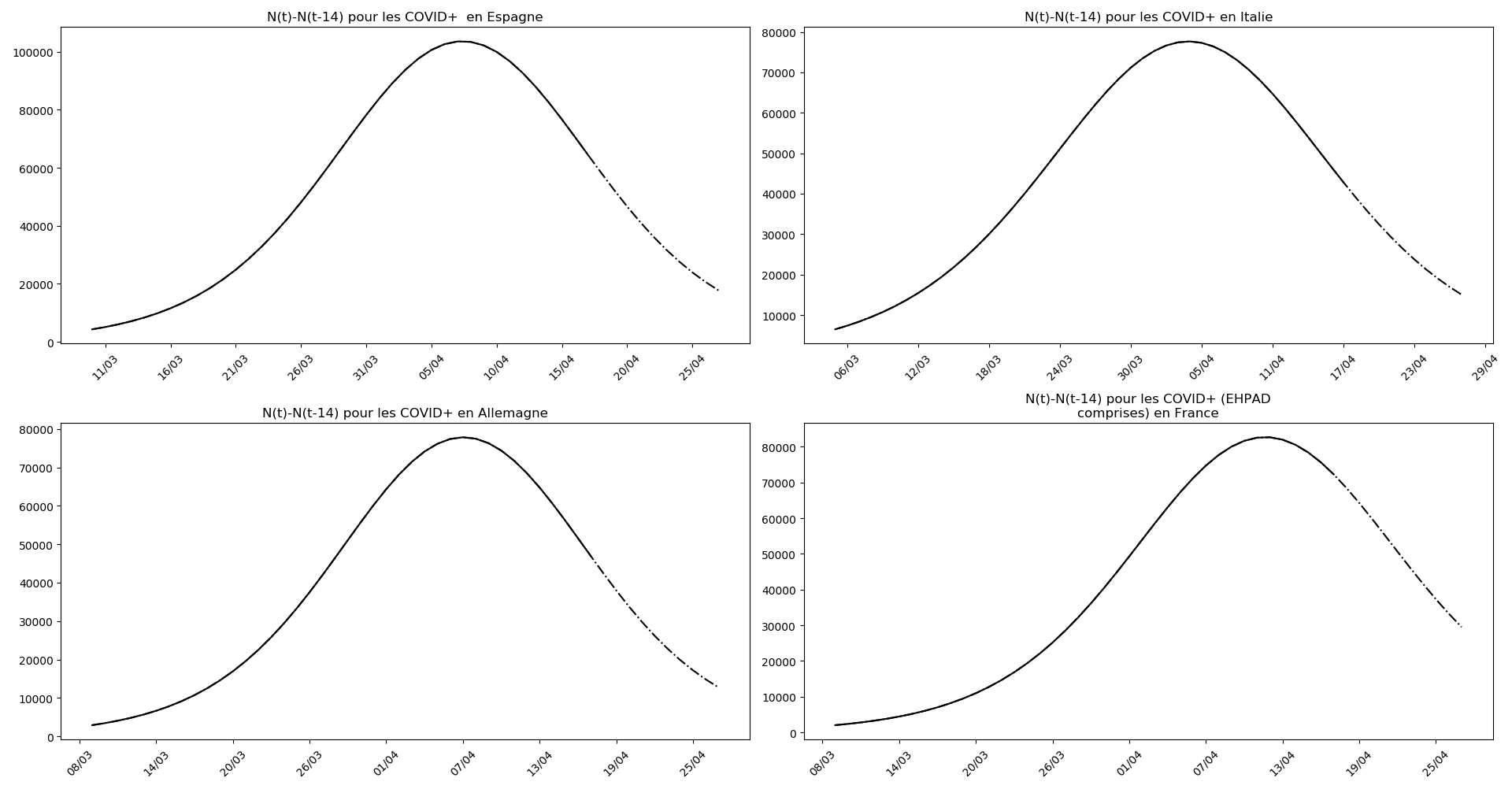
def evol_pic(debd, dt, n, a, b, c, typeDonnees, sbp = None):
    Delta = 14
    inter = (n+dt-Delta)//10+1
    figDate(sbp=sbp,intervalle = inter)
    dates = [dtm.datetime.fromordinal(737448+debd+k+Delta) for k in range(n+dt-Delta)]
    dates = [str(k.day)+'/'+str(k.month)+'/'+str(k.year) for k in dates]
    lbl = [dtm.datetime.strptime(d,"%d/%m/%Y").date().toordinal() for d in dates]
    XX = np.array(range(Delta,n+dt),dtype=np.float64)
    YY = f(a,b,c)(XX)-f(a,b,c)(XX-Delta)
    plt.plot(lbl,YY,'-.k')
    XX = np.array(range(Delta,n),dtype=np.float64)
    YY = f(a,b,c)(XX)-f(a,b,c)(XX-Delta)
    plt.plot(lbl[:-dt],YY,'k')
    plt.xticks(rotation = 45)
    plt.title('N(t)-N(t-'+str(Delta)+') pour les '+typeDonnees )
    
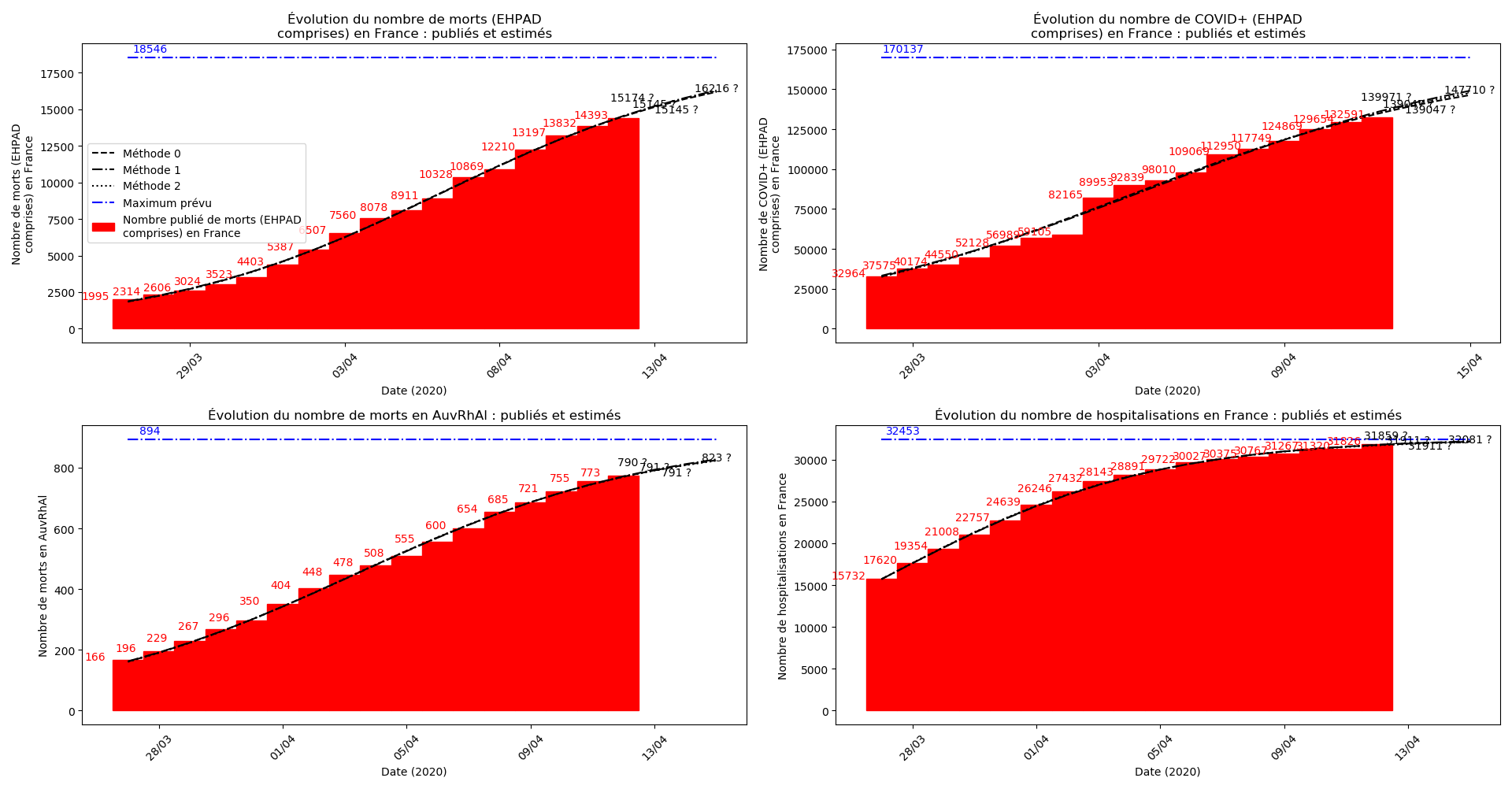
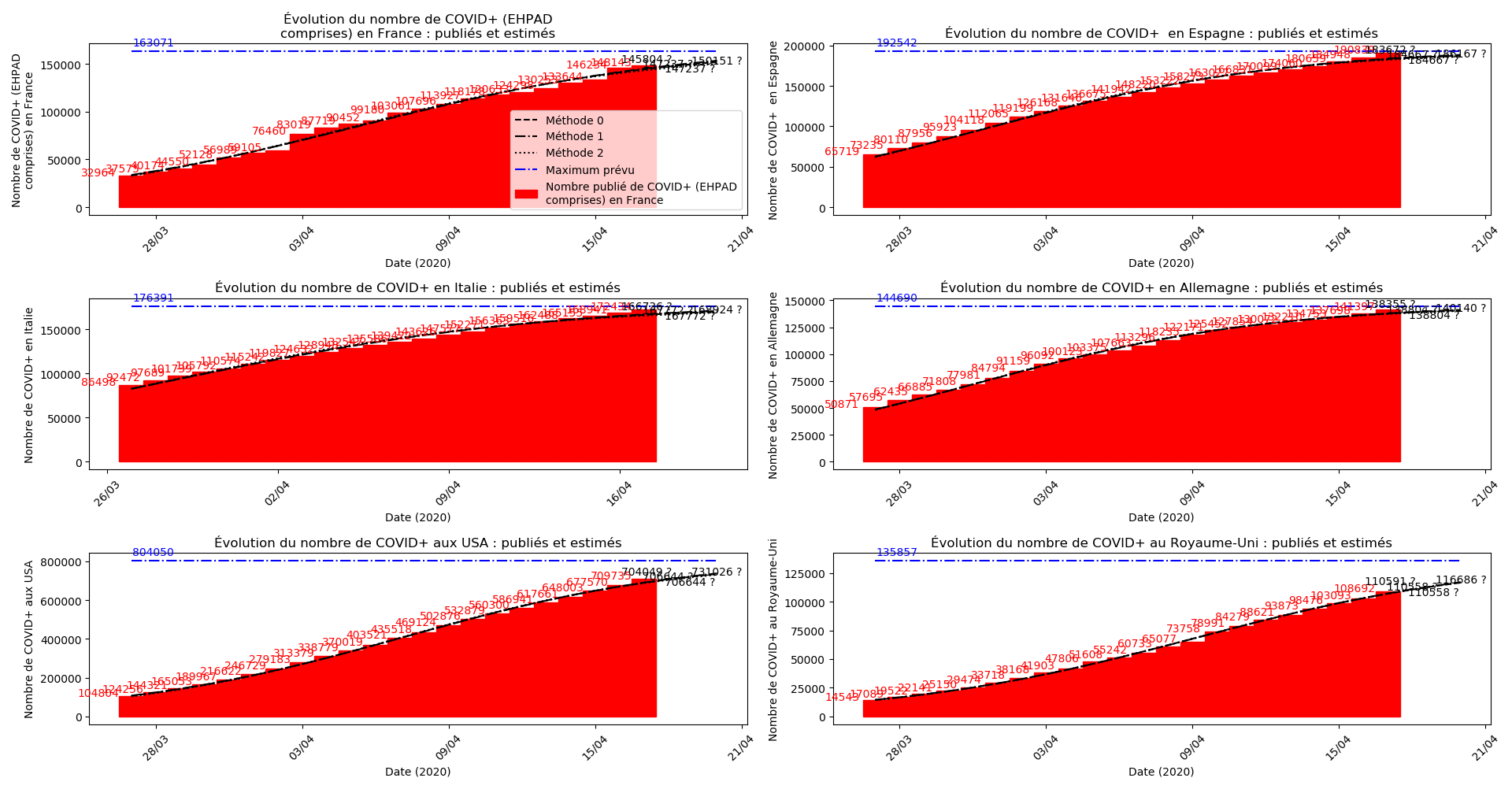
def evol_cas(dates, liste, somcum, debd, debf, dt, typeDonnees, asymp,
             sbp = None, legend=True):
    am,a,aM,bm,b,bM,cm,c,cM = liste
    aa,bb,cc = asymp
    n=len(somcum)
    inter = (n+dt)//10+1
    if sbp == None:
        plt.figure()
        ax = plt.gca()
        formatter = mdates.DateFormatter("%d/%m")
        ax.xaxis.set_major_formatter(formatter)
        locator = mdates.DayLocator(interval = inter)
        ax.xaxis.set_major_locator(locator)
    else:
        plt.subplot(sbp)
        ax = plt.gca()
        formatter = mdates.DateFormatter("%d/%m")
        ax.xaxis.set_major_formatter(formatter)
        locator = mdates.DayLocator(interval = inter)
        ax.xaxis.set_major_locator(locator)
    # Histogrammes du nombre publié de morts
    dates = [dtm.datetime.fromordinal(737447+debd+debf+k) for k in range(n+1-debf)]
    dates = [str(k.day)+'/'+str(k.month)+'/'+str(k.year) for k in dates]
    lbl = [dtm.datetime.strptime(d,"%d/%m/%Y").date() for d in dates]
    for k,l in zip(somcum[debf:],lbl[:-1]):
        m = mpat.Rectangle((l.toordinal()+0.5,0),1,k,color='red')
        ax.add_patch(m)
        plt.annotate(k, (l.toordinal()+1,k), textcoords="offset points",
                     xytext=(-30,0), ha='center', color='red')
    # Affichage de la régression sigmoïdale
    dates = [dtm.datetime.fromordinal(737448+debd+debf+k) for k in range(n+dt-debf)]
    dates = [str(k.day)+'/'+str(k.month)+'/'+str(k.year) for k in dates]
    lbl = [dtm.datetime.strptime(d,"%d/%m/%Y").date().toordinal() for d in dates]
    XX = np.array(range(debf,n+dt),dtype=np.float64)
    YY2 = f(am,bm,cm)(XX)
    plt.plot(lbl,YY2,'--k')
    plt.annotate(str(int(round(YY2[-dt])))+' ?', (lbl[-dt],int(YY2[-dt])), 
                 textcoords="offset points", xytext=(20,-5),
                 ha='center', color='black')
    YY = f(a,b,c)(XX)
    plt.plot(lbl,YY,'-.k')
    plt.annotate(str(int(round(YY2[-dt])))+' ?', (lbl[-dt],int(YY2[-dt])), 
                 textcoords="offset points", xytext=(0,0),
                 ha='center', color='black')
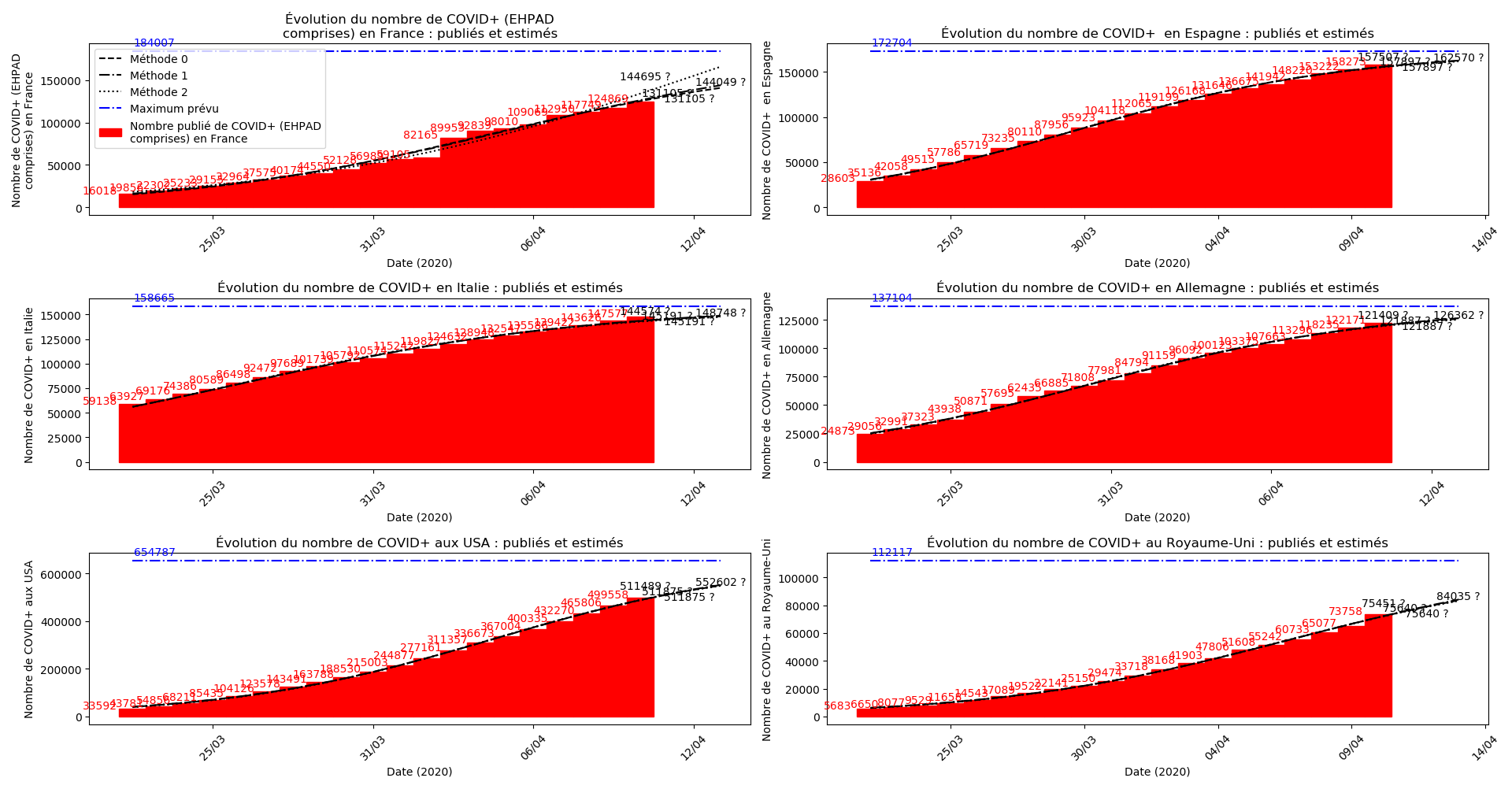
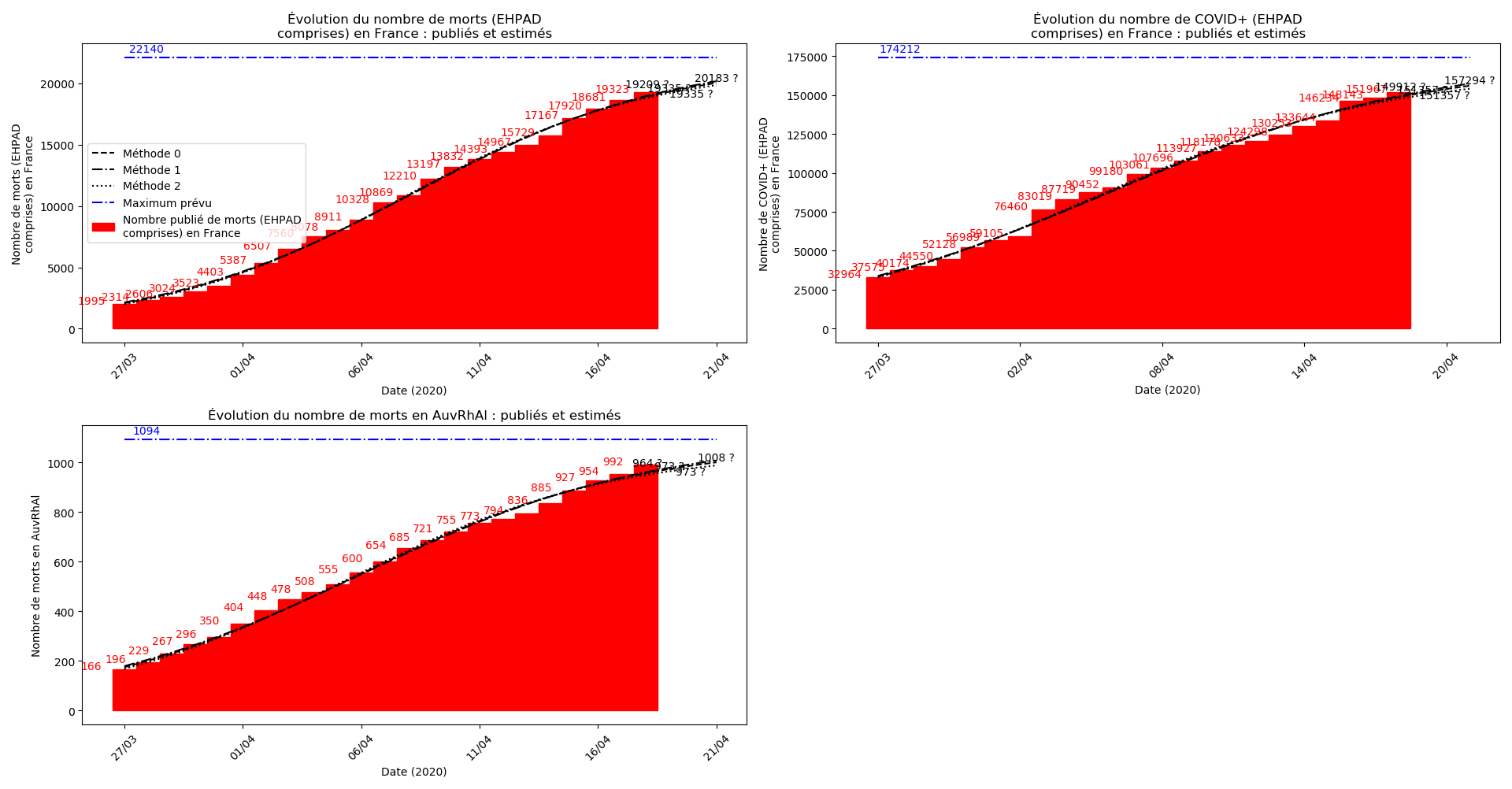
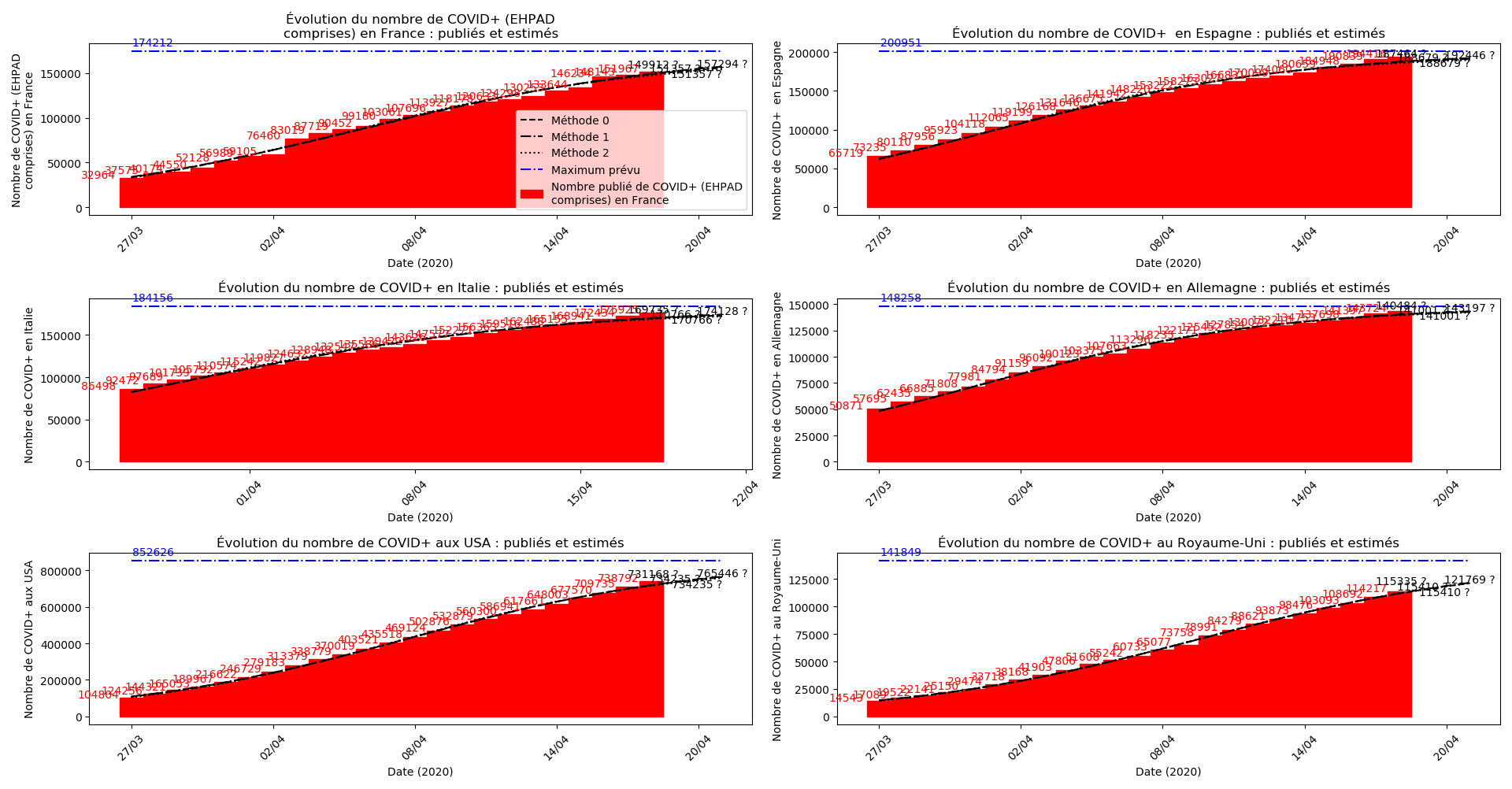
    plt.title(u"Évolution du nombre de "+typeDonnees+u" : publiés et estimés")
    plt.xlabel("Date (2020)")
    plt.ylabel('Nombre de '+typeDonnees)
    YY2 = f(aM,bM,cM)(XX)
    plt.plot(lbl,YY2,':k')
    plt.plot(lbl,0*YY2+cc,'-.b')
    plt.annotate(str(int(round(cc))), (lbl[0],int(cc)), 
                 textcoords="offset points", xytext=(20,5),
                 ha='center', color='blue')
    plt.annotate(str(int(round(YY2[-dt])))+' ?', (lbl[-dt],int(YY2[-dt])), 
                 textcoords="offset points", xytext=(-20,5),
                 ha='center', color='black')
    YY2 = f(aa,bb,cc)(XX)
    plt.annotate(str(int(round(YY2[-1])))+' ?', (lbl[-1],int(YY2[-1])), 
                 textcoords="offset points", xytext=(0,0),
                 ha='center', color='black')
    plt.xticks(rotation = 45)
    if legend:
        plt.legend([u"Méthode 0",
                u"Méthode 1",
                u"Méthode 2",
                u"Maximum prévu",
                u"Nombre publié de "+typeDonnees])


def repGraph(S0, debutDonnees, debutSimul, finSimul, typeDonnees, nouveaux, L,
             typ=[], sbp=None, legend=True, method=2):
    # S0 : nombre de cas constatés avant le début des données
    # debutDonnees : nombre de jours entre le 22 janvier 2020 et les debut
    # des données
    # debutSimul : nombre de jours entre le début des données et le début 
    # de la simulation
    # finSimul : nombre de jours entre la fin des données et la fin de la
    # simulation
    # typeDonnees : chaîne de caractères décrivant les données
    # nouveaux : données sous la forme du nombre de nouveaux cas quotidiens
    n = len(nouveaux)
    debf = debutSimul
    debd = debutDonnees
    dt = finSimul
    Lam, La, LaM, Lbm, Lb, LbM, Lcm, Lc, LcM = L
    am,a,aM,bm,b,bM,cm,c,cM = Lam[-1],La[-1],LaM[-1],Lbm[-1],\
                              Lb[-1],LbM[-1],Lcm[-1],Lc[-1],LcM[-1]
    if method==0:
        aa,bb,cc = am,bm,cm
        Laa,Lbb,Lcc = Lam,Lbm,Lcm
    elif method==1:
        aa,bb,cc = a,b,c
        Laa,Lbb,Lcc = La,Lb,Lc
    else:
        aa,bb,cc = aM,bM,cM
        Laa,Lbb,Lcc = LaM,LbM,LcM
    dates = [dtm.datetime.fromordinal(737447+debd+k) for k in range(debf,n+1)]
    if (not typ)or(0 in typ): 
        evol(dates,(Lam,La,LaM),
         u"Evolution du paramètre a de l'interpolation avec le temps",
         typeDonnees, sbp=sbp, legend=legend)
    if (not typ)or(1 in typ): 
        evol(dates,(Lbm,Lb,LbM),
         u"Evolution du paramètre b de l'interpolation avec le temps",
         typeDonnees, sbp=sbp, legend=legend)
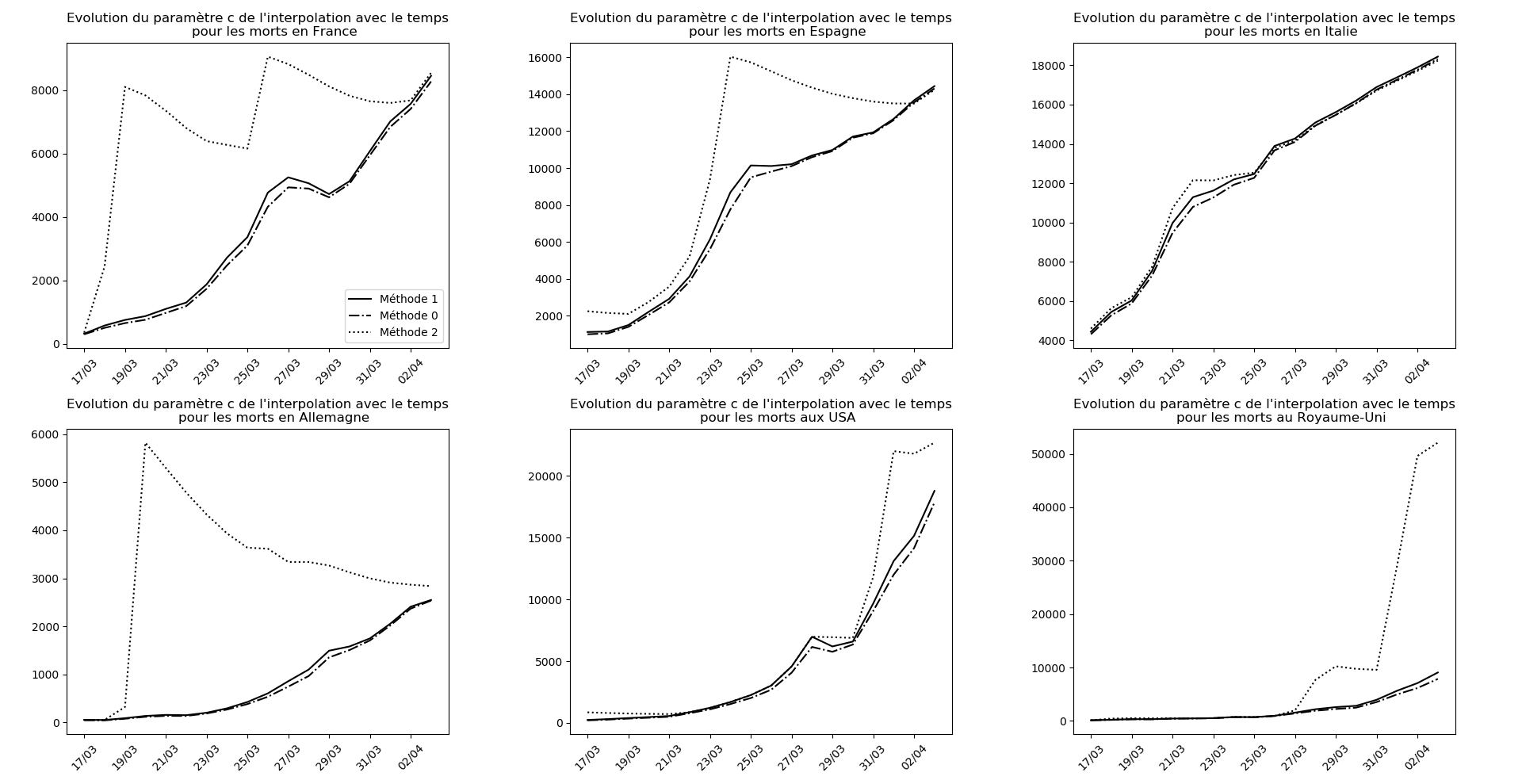
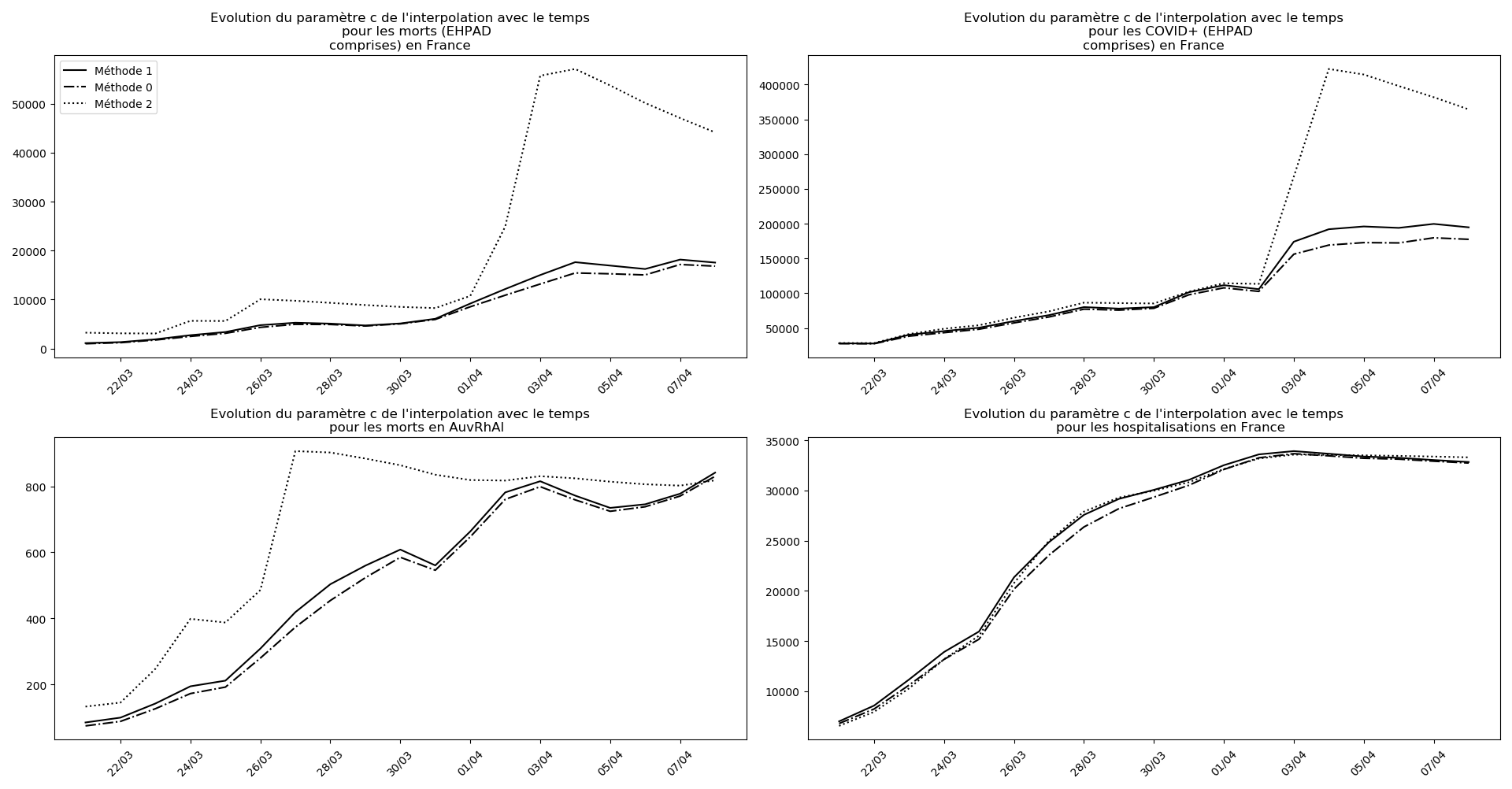
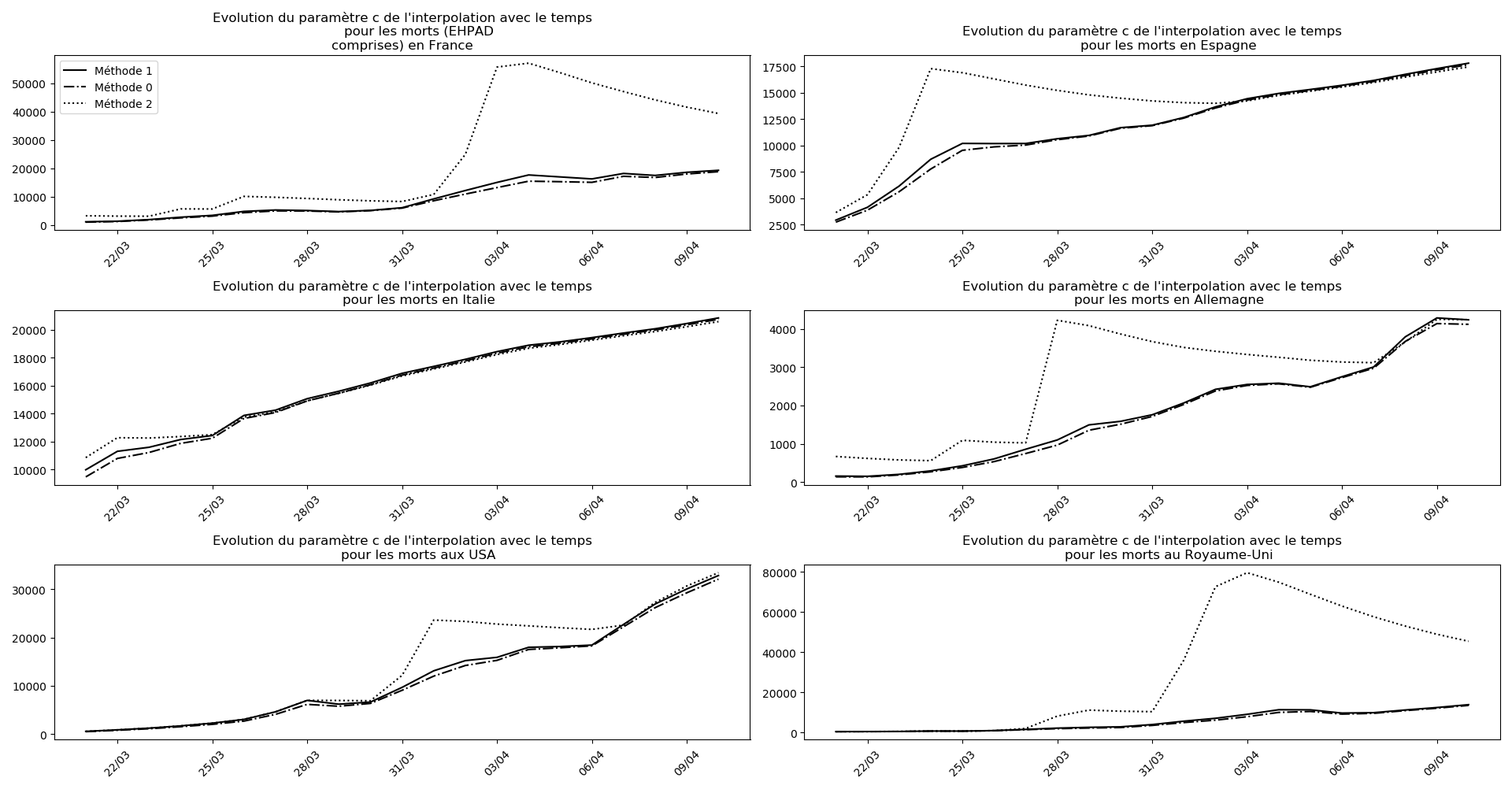
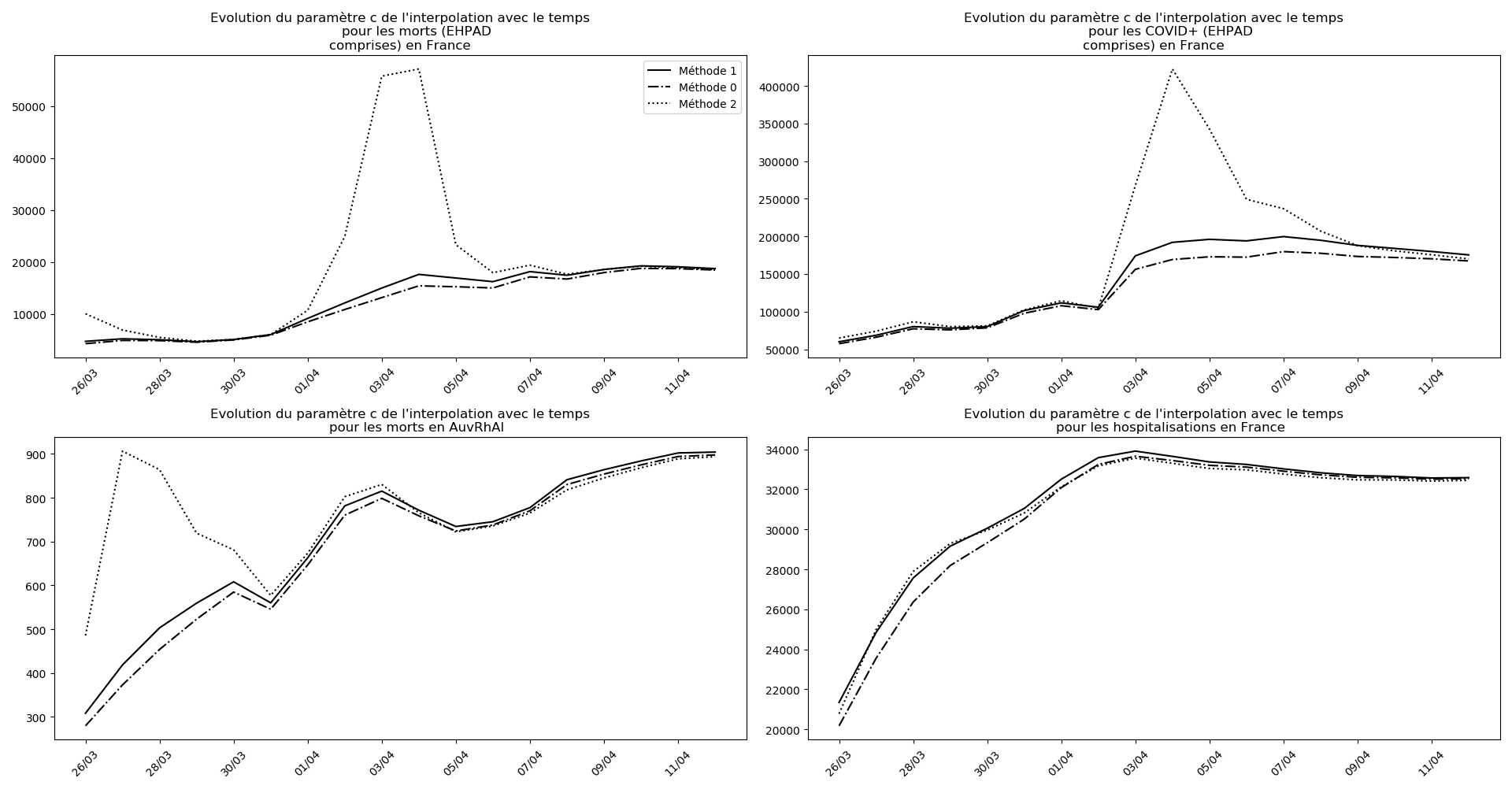
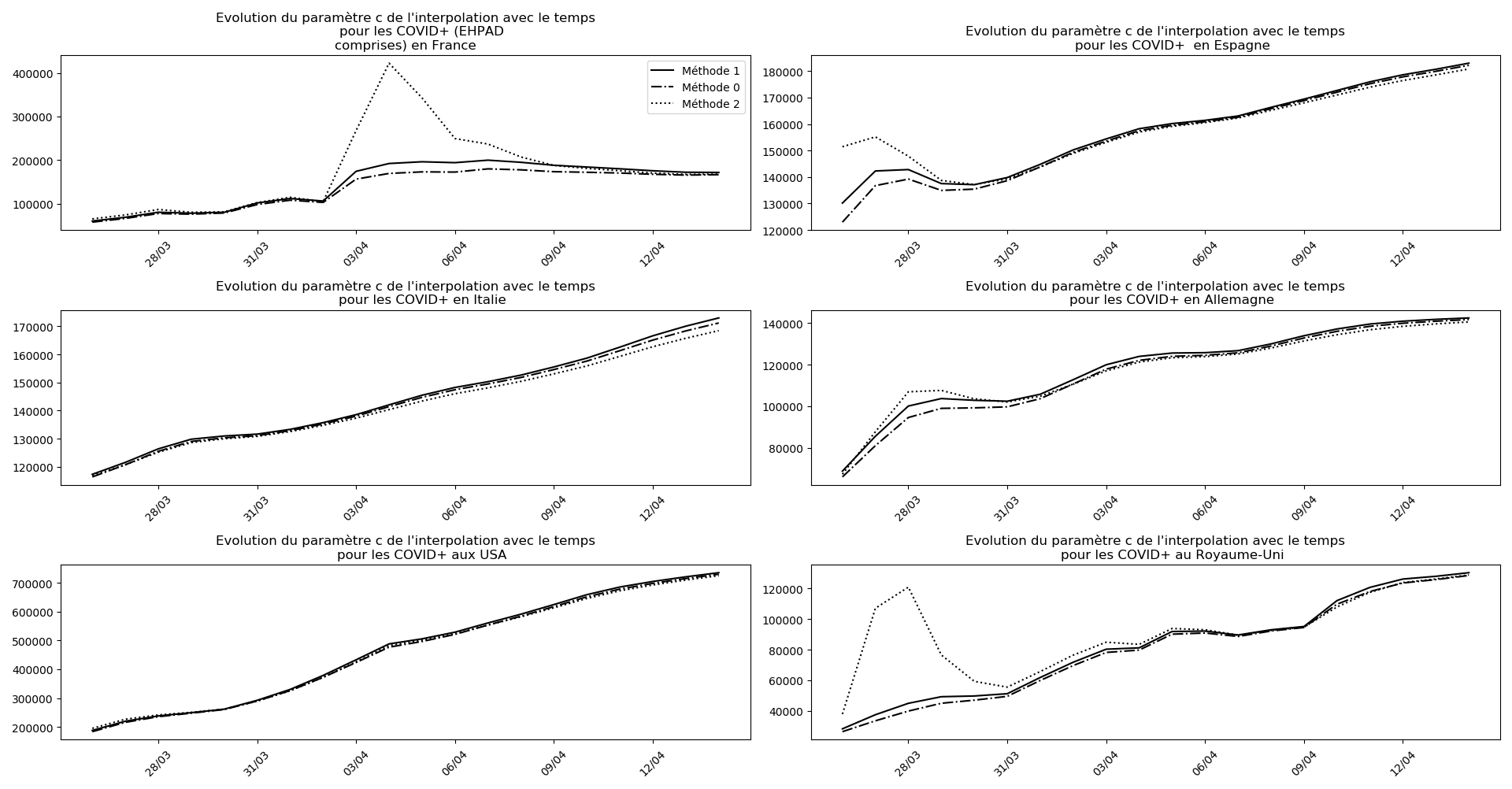
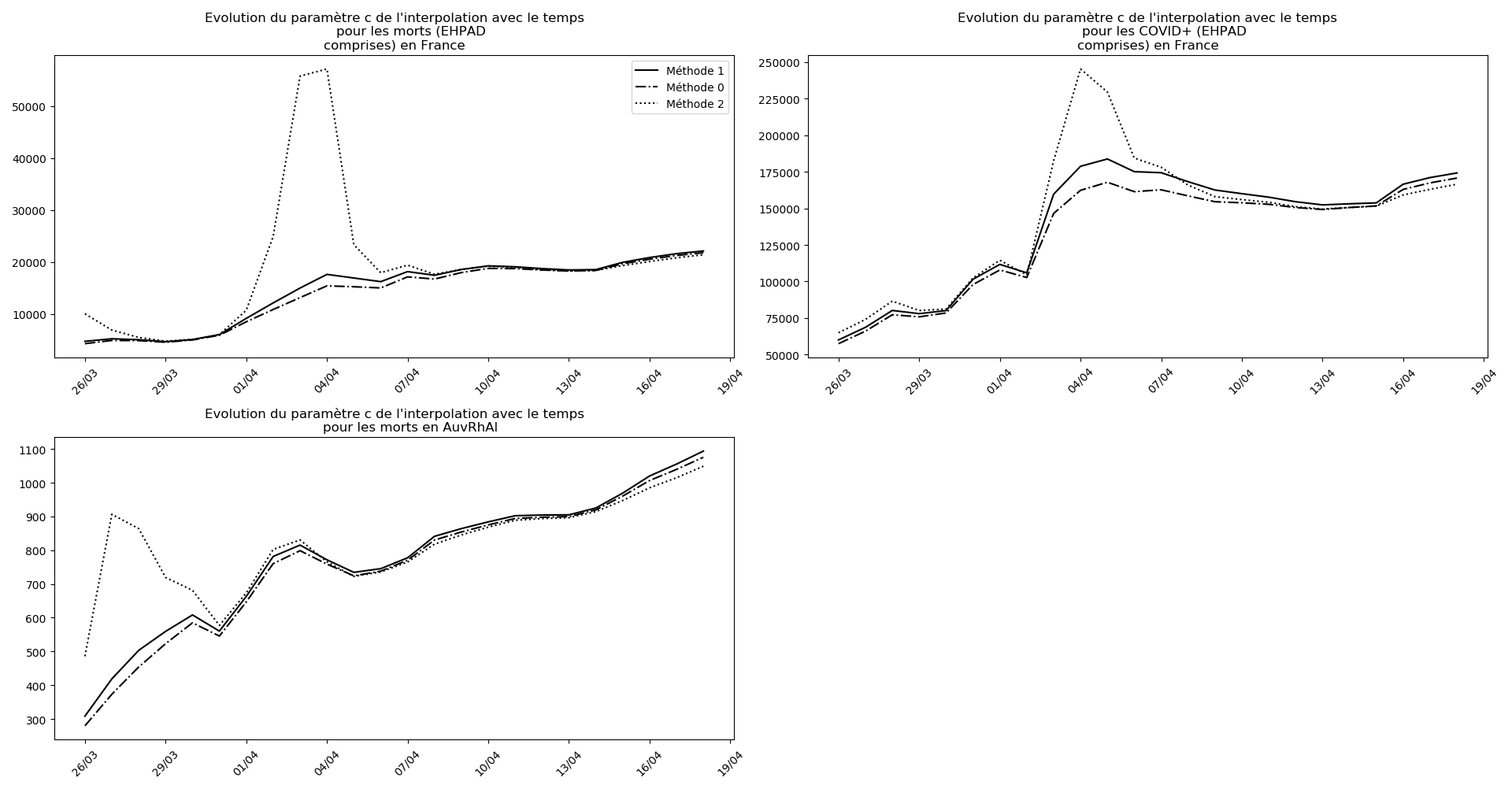
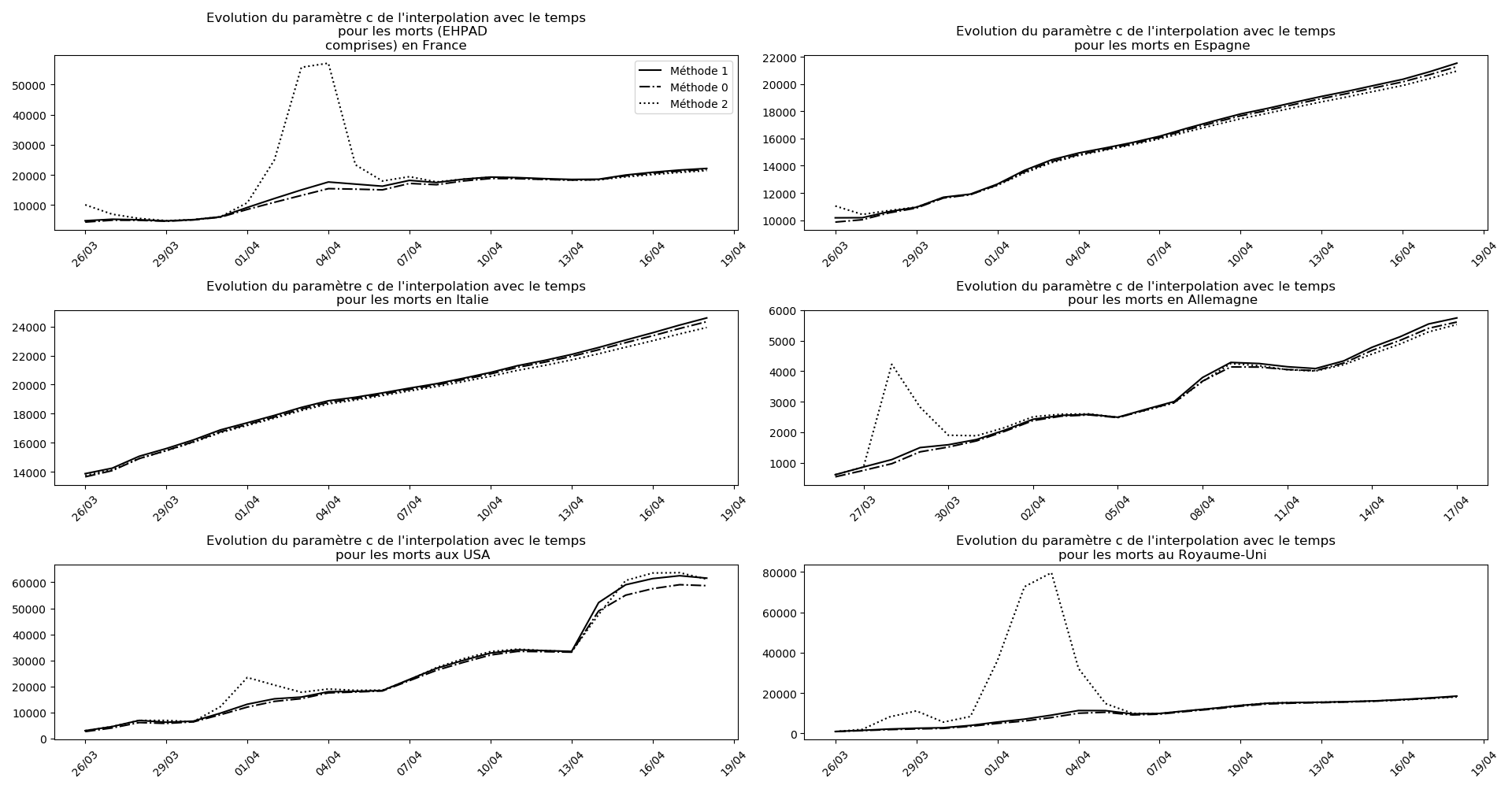
    if (not typ)or(2 in typ): 
        evol(dates,(Lcm,Lc,LcM),
         u"Evolution du paramètre c de l'interpolation avec le temps",
         typeDonnees,sbp=sbp, legend=legend)
    
    carac = [caracteristiques(Laa[i],Lbb[i],Lcc[i],debf+i) for i in range(n-debf+1)]
    T1 = [k[0] for k in carac]
    T2 = [k[1] for k in carac]
    T3 = [dtm.datetime.fromordinal(int(round(k[2]))+737448+debd) for k in carac]
    if (not typ)or(3 in typ): 
        evol_taux(dates, T1, T2,typeDonnees, sbp=sbp, legend=legend)
    if (typ is None)or(4 in typ):     
        evol_inflexion(dates, T3,typeDonnees, sbp=sbp)
    
    somcum = [S0+sum(nouveaux[:(k+1)]) for k in range(n)]
    if (not typ)or(5 in typ): 
        evol_previsions(dates, (Lam,La,LaM,Lbm,Lb,LbM,Lcm,Lc,LcM), nouveaux,
                    somcum, debf, typeDonnees,sbp=sbp, legend=legend)
    if (not typ)or(6 in typ): 
        evol_cas(dates, (am,a,aM,bm,b,bM,cm,c,cM), somcum, debd, debf, dt, 
                 typeDonnees, (aa,bb,cc), sbp=sbp, legend=legend)
    if (not typ)or(7 in typ):
        evol_pic(debd, dt,n,aa,bb,cc,typeDonnees, sbp=sbp) 

class covid():
    def __init__(self,datas):
        self.datas = [list(datas)]
        self.L = [{}]
    
    def add(self,datas):
        self.datas.append(list(datas))
        self.L.append({})
    
    def setDt(self,dt):
        for k in self.datas:
            k[3] = dt
    
    def calc(self,lst,err=2,prec=1e-3):
        for k in lst:
            if self.L[k]:
                continue
            S0, debutDonnees, debutSimul, finSimul, typeDonnees, nouveaux = self.datas[k]
            n = len(nouveaux)
            debf = debutSimul
            La, Lam, LaM = [], [], []
            Lb, Lbm, LbM = [], [], []
            Lc, Lcm, LcM = [], [], []
            mxc = 0
            for fin in range(debf,n+1):
                ((am,bm,cm),(a,b,c),(aM,bM,cM)) = interpSigm(nouveaux,fin,S0=S0,
                                                             mxS=7e7, mxc = mxc,
                                                             prec = prec)
                La.append(a)
                Lam.append(am)
                LaM.append(aM)
                Lb.append(b)
                Lbm.append(bm)
                LbM.append(bM)
                Lc.append(c)
                Lcm.append(cm)
                LcM.append(cM)
                mxc = cM
            self.L[k] = (Lam, La, LaM, Lbm, Lb, LbM, Lcm, Lc, LcM)
            
    
    def repGraph(self, k, typ=[], prec = 1e-5, method=2):
        self.calc([k], prec=prec)
        repGraph(*self.datas[k],self.L[k],typ=typ, method = method)
    
    def compare(self, typ, which=None, prec = 1e-5, method = 2):
        fig = plt.figure()
        plt_set_fullscreen()
        fig.set_tight_layout(True)
        assert isinstance(typ,int) and 0<=typ<=7, "typ doit être un entier"
        n = len(self.datas)
        if not which:
            which=range(n)
        self.calc(which, prec=prec)
        n = len(which)
        p = round(np.sqrt(n+1))
        a = p*100 + (n//p+(n%p>0))*10
        for k in range(len(which)):
            repGraph(*self.datas[which[k]],self.L[which[k]], typ=[typ],
                     sbp=a+k+1,legend=(k==0),method=method)
    
    def multi(self, typ, which, prec = 1e-5, method = 2):
        fig = plt.figure()
        plt_set_fullscreen()
        fig.set_tight_layout(True)
        assert len(typ)==len(which),"typ et which doivent être deux listes de même taille"
        n = len(typ)
        self.calc(which, prec=prec)
        p = round(np.sqrt(n+1))
        a = p*100 + (n//p+(n%p>0))*10
        for k in range(len(which)):
            repGraph(*self.datas[which[k]],self.L[which[k]], typ=[typ[k]],
                     sbp=a+k+1,legend=True,method=method)
    
    def fiabilite(self, which=None, prec = 1e-5, ponderation = True,
                  method = 2):
        n = len(self.datas)
        if not which:
            which=range(n)
        self.calc(which, prec=prec)
        R=[]
        for k in which:
            S0, debd, debs, fins, typed, data = self.datas[k]
            a,b,c = self.L[k][method][-1], self.L[k][method+3][-1],\
                    self.L[k][method+6][-1]
            n = len(data)
            somcum = np.array([S0+sum(data[:(k+1)]) for k in range(n)],dtype=np.float64)
            X = np.array(range(n),dtype=np.float64)
            if ponderation:
                poids = somcum**2*(1-somcum/c)**2
                poids = poids/np.sum(poids)
            else:
                poids = 1/n
            N = np.sum(poids*(somcum-f(a,b,c)(X))**2)
            D = np.sum(poids*somcum**2)
            R.append([typed,(1-N/D)**0.5])
        return R

Utilisation

Pour utiliser l’algorithme, il suffit de déclarer un objet de la classe covid de la façon suivante :

Cov = covid((4, # nombre de cas avant la série de données
             40, # nombre de jours entre le 22 janvier et le premier jour de la série
             18, # nombre de jours entre le 1er jour de la série et le début de la simul
             3, # nombre de jours simulés après la fin de la série
             "morts en France", # chaine représentant la série
          [0, 3, 2, 7, 3, 11, 3, 15, 13, 18, 12, 36, 21, 27, 89, 108, 78, 112,
            112, 186, 240, 231, 365, 299]))

Puis d’utiliser l’une des méthodes de la classe permettant de faire des représentations graphiques.

Situation au 3 avril

France

Sources des données :

Monde

Source des données :

https://www.worldometers.info/coronavirus/

Situation au 4 avril

Les graphiques du jour nécessitent d’être commentés. Je commence par faire le point sur mes sources.

J’utilise essentiellement deux sources non-gouvernementales pour les données internationales de cas confirmés CoViD-19 et de décès liés à la maladie :

Le second lien utilise lui-même le premier lien comme source, mais il présente aussi un détail par département français que le premier ne donne pas.

J’utilise aussi des sources gouvernementales françaises :

Le second est une énorme base de données sous forme de fichiers csv, plutôt mal hiérarchisée, dans laquelle j’ai encore du mal à me retrouver. Notamment, je ne parviens toujours pas à trouver les données spécifiques concernant les cas confirmés et les décès en EHPAD liés au CoViD-19 puisque le gouvernement français a décidé de faire deux dénombrements séparés suivant que les malades vivent ou non en EHPAD.

France

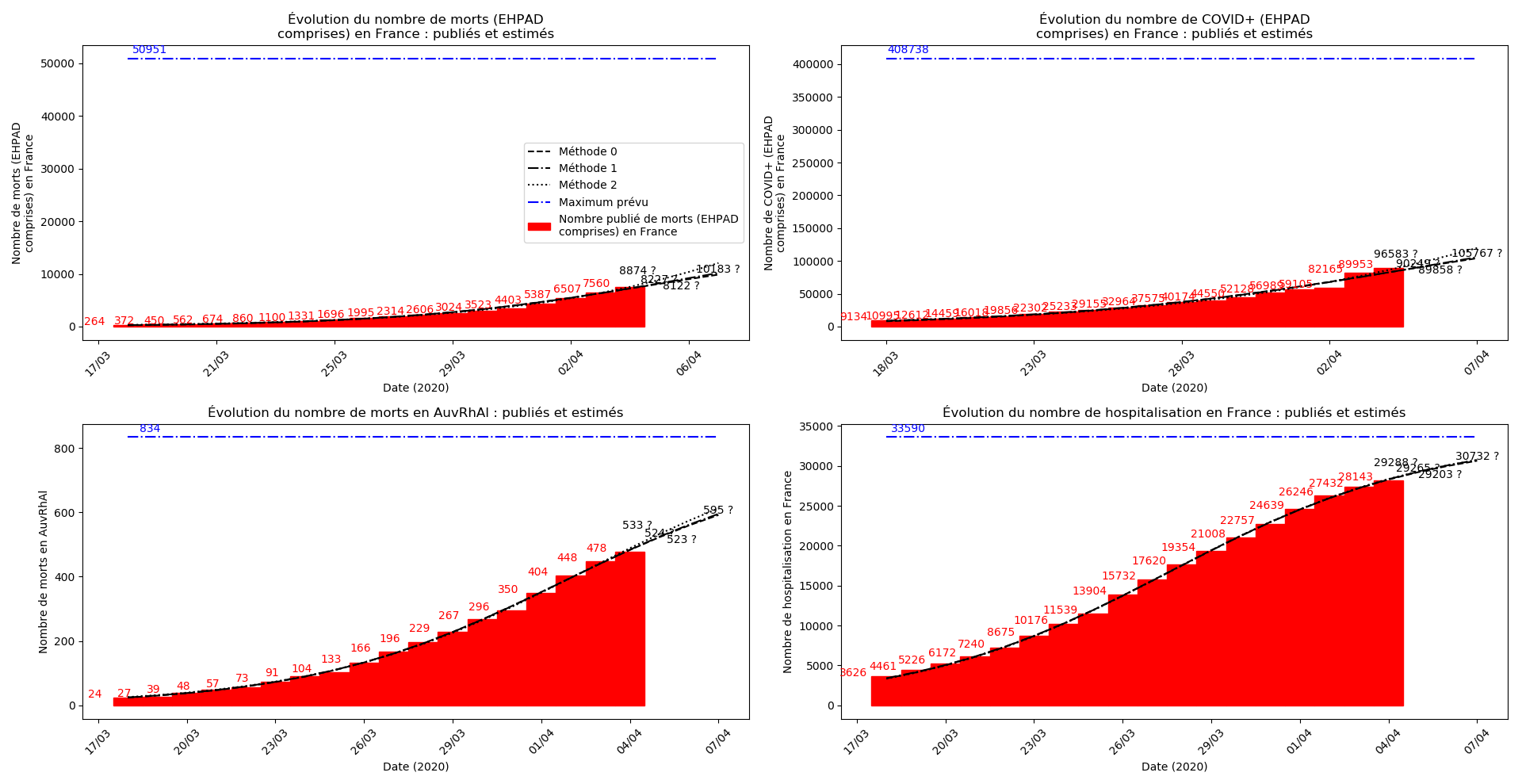
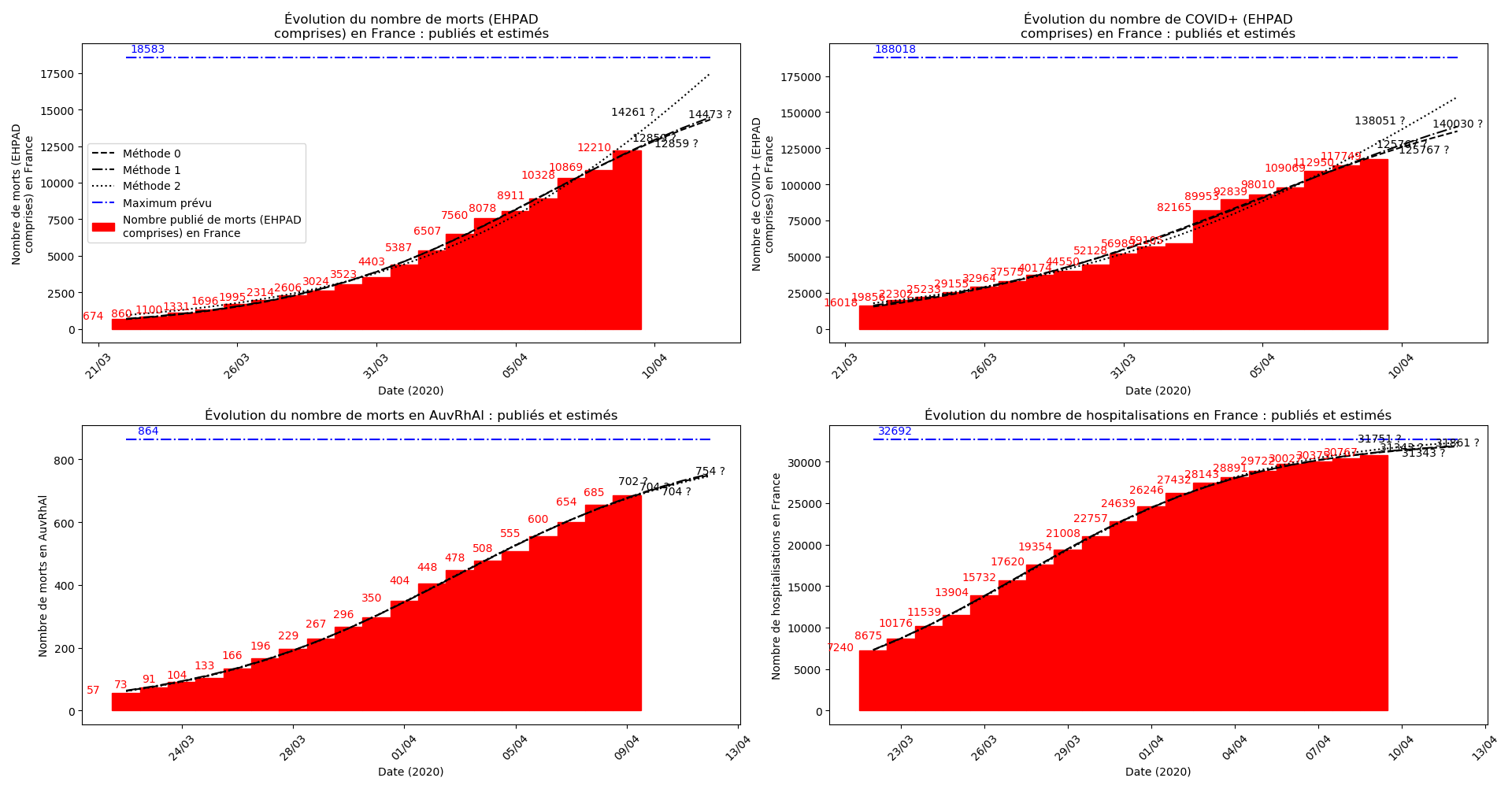
Les sites gouvernementaux donnent désormais (depuis ~~hier à ma connaissance~~ le 1^er avril - j’ai mis à jour les graphiques) le nombre de décès en EHPAD à côtés du nombre de décès hors EHPAD. Le nombre de décès en EHPAD représente plus du quart du nombre de décès total, ce qui n’a donc rien de négligeable. Je ne parviens pas à obtenir la chronologie de ces décès (et des CoViD+) en EHPAD mais j’ai décidé, contrairement au gouvernement, de ne pas faire deux comptes séparés.

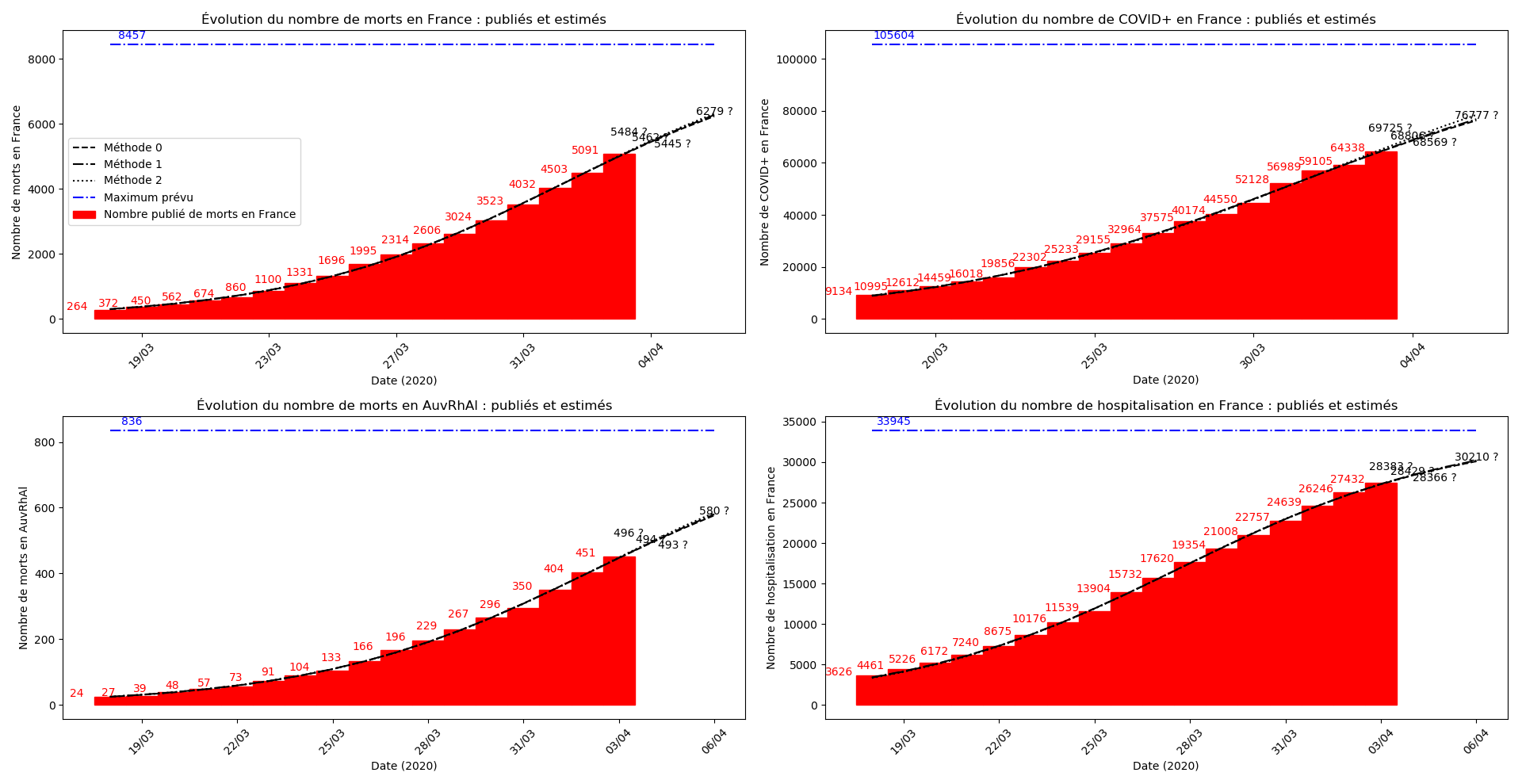
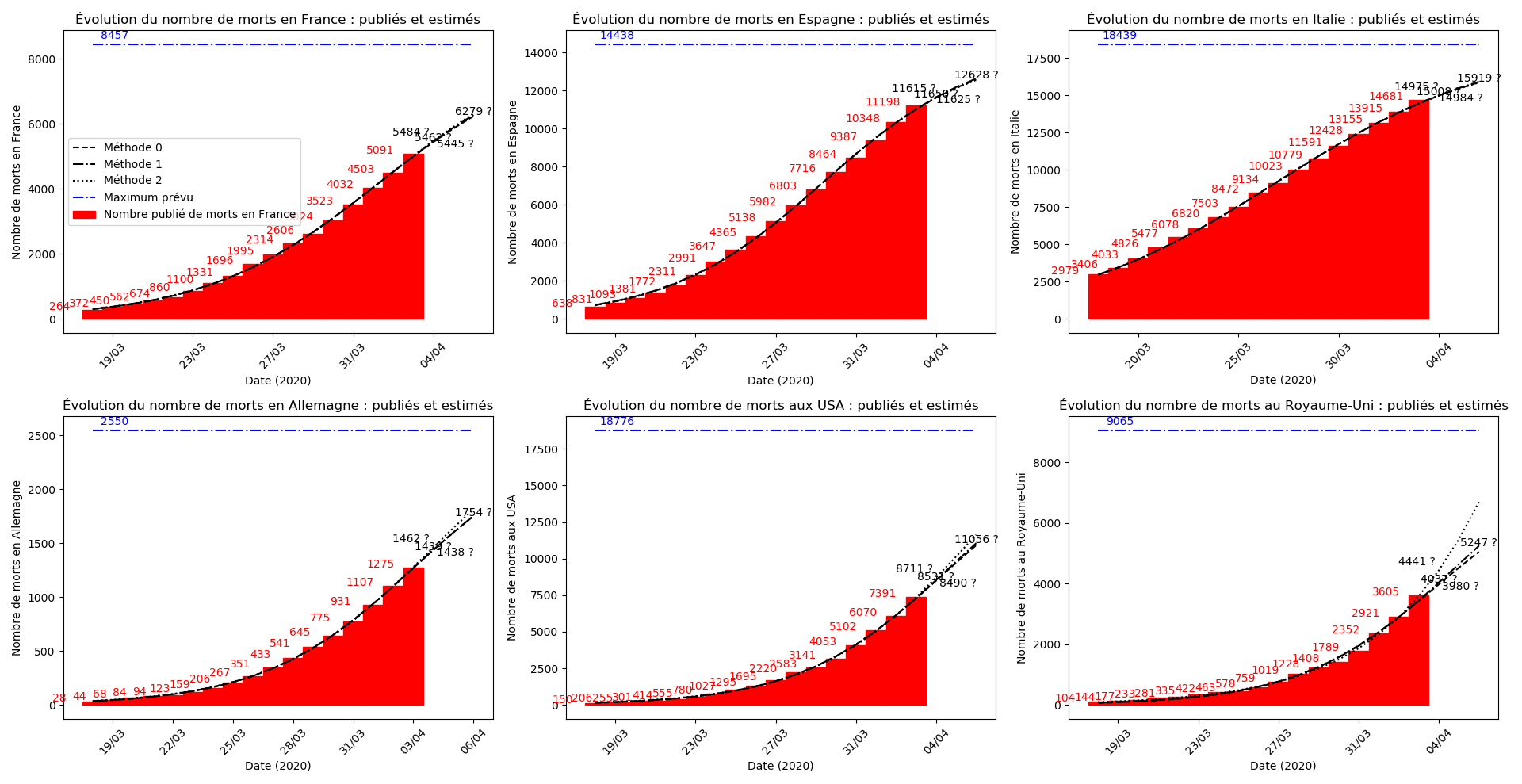
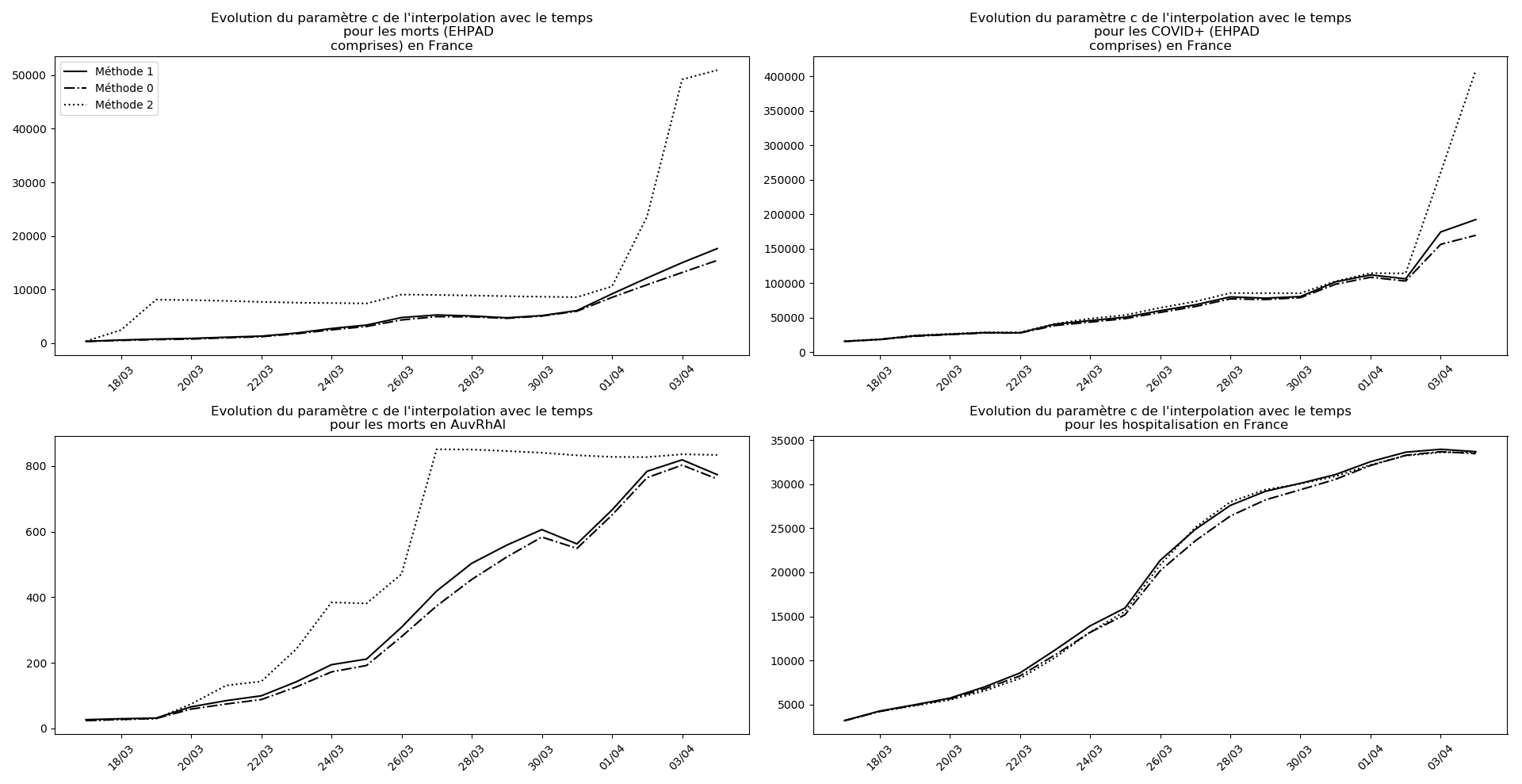
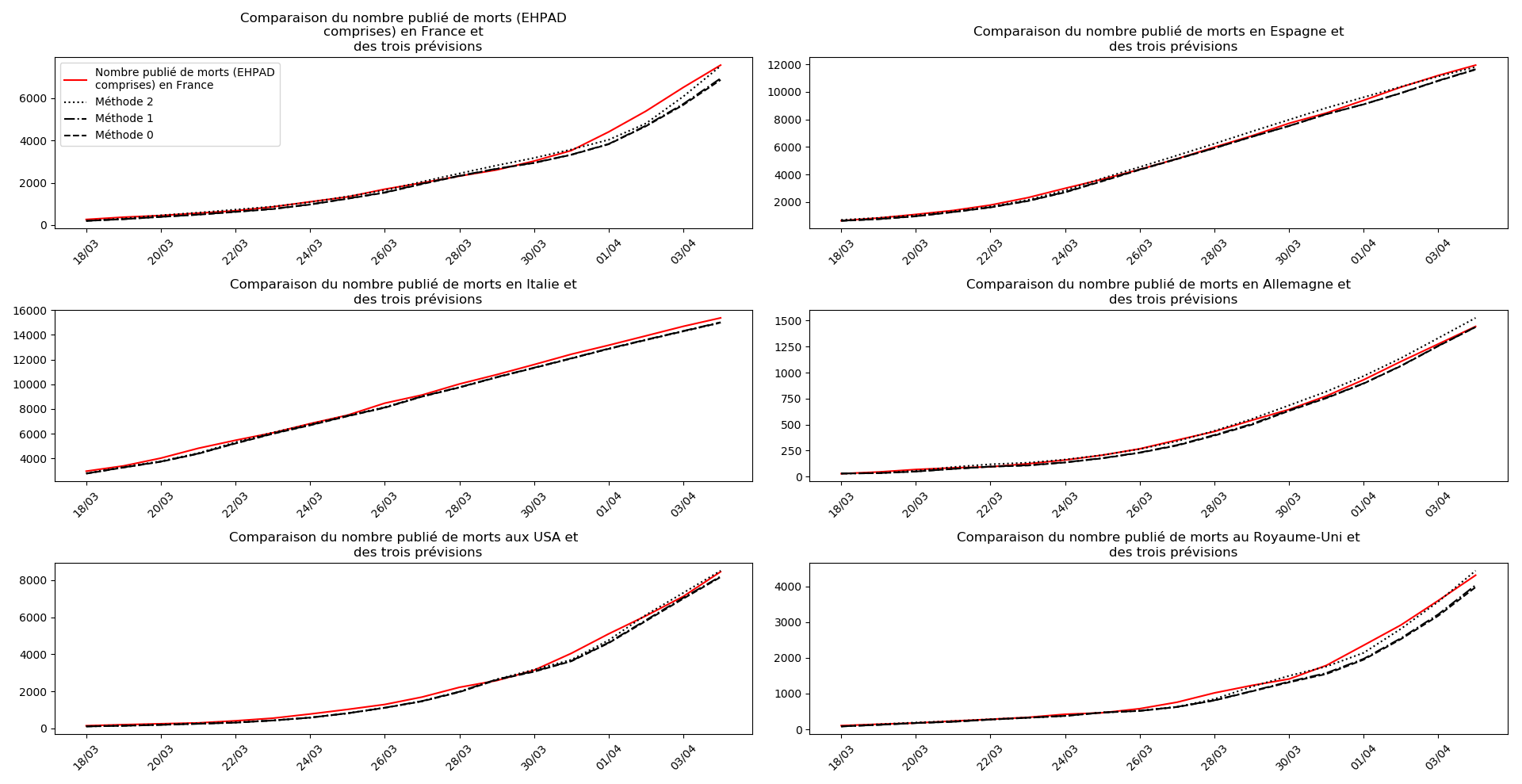
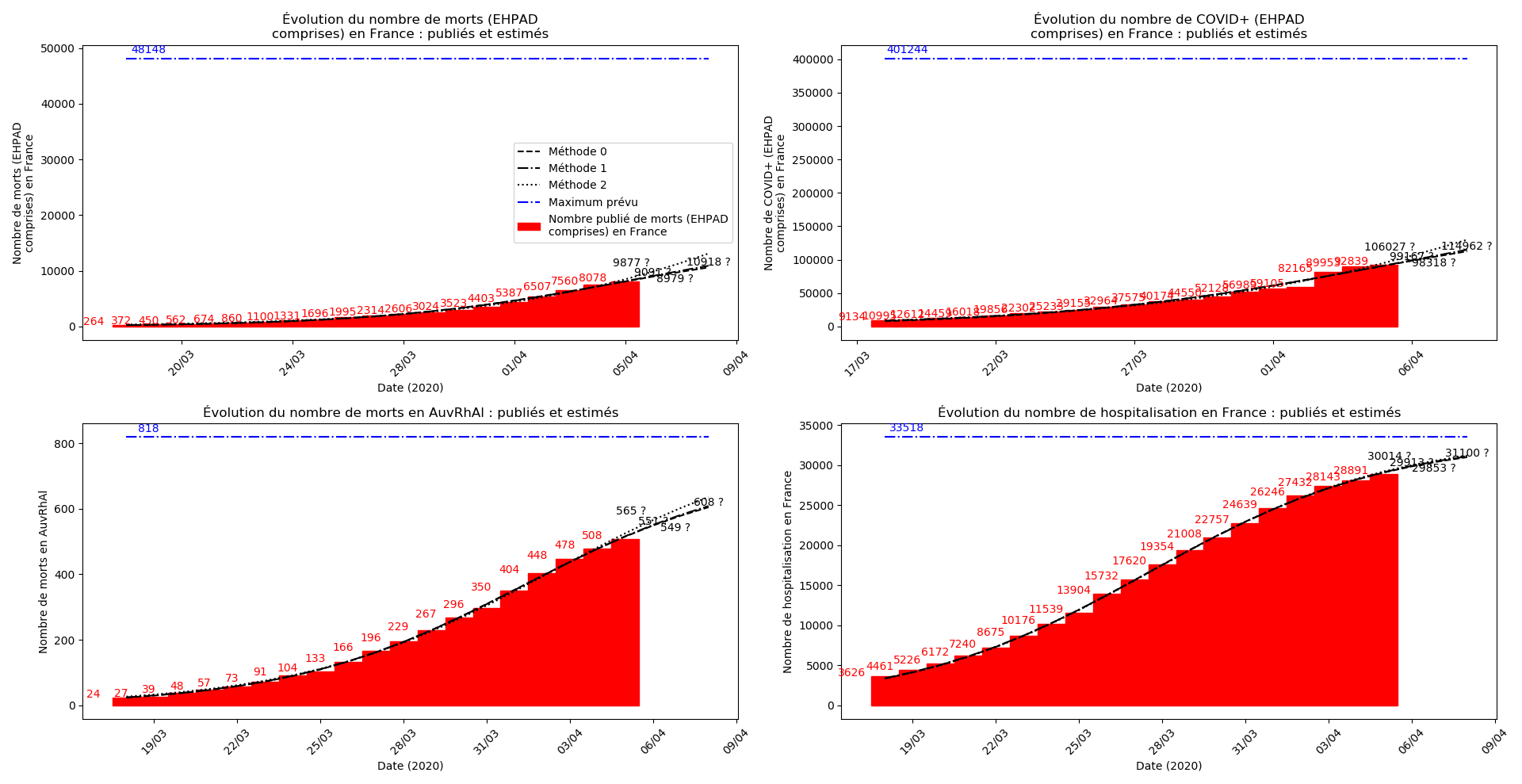
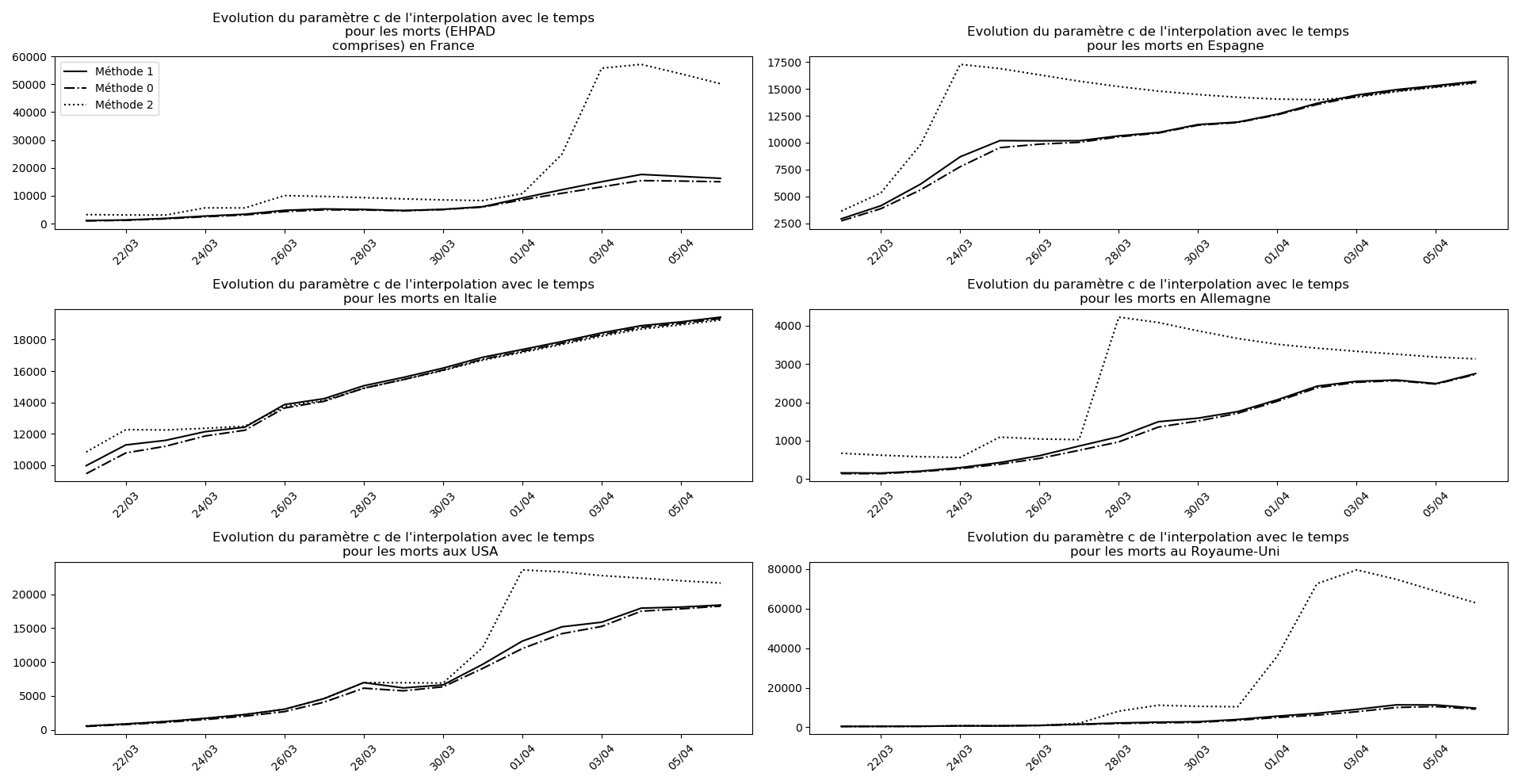
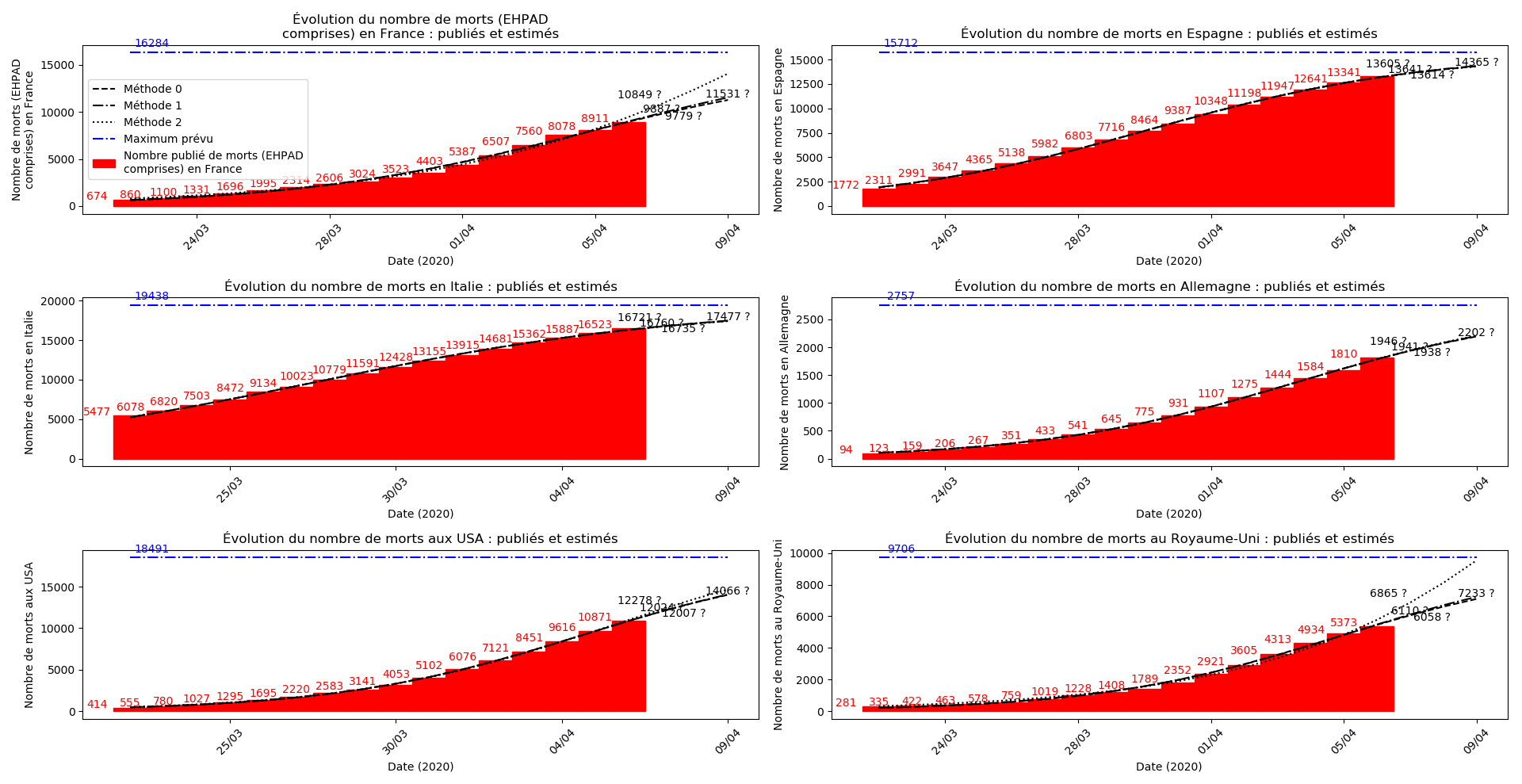
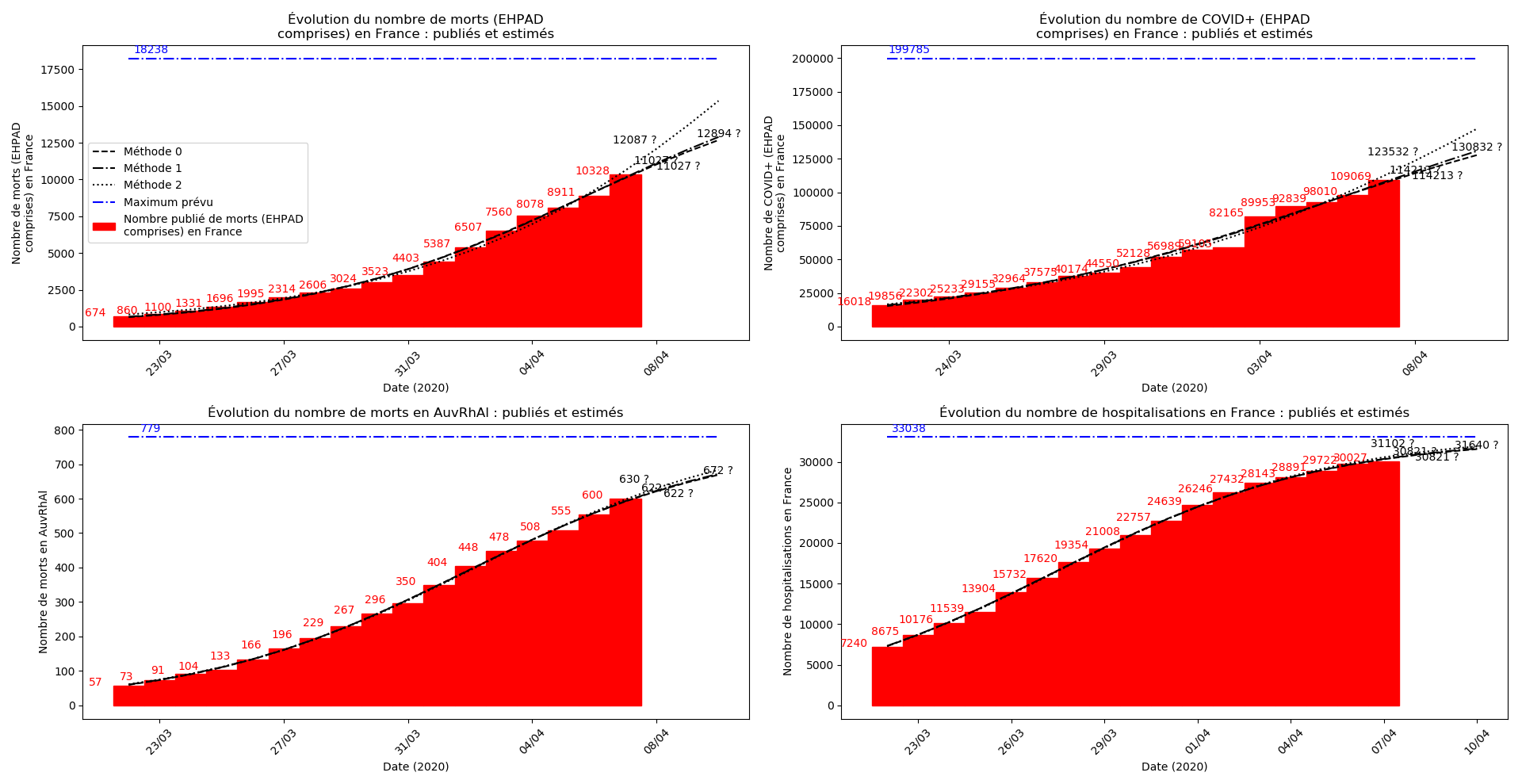
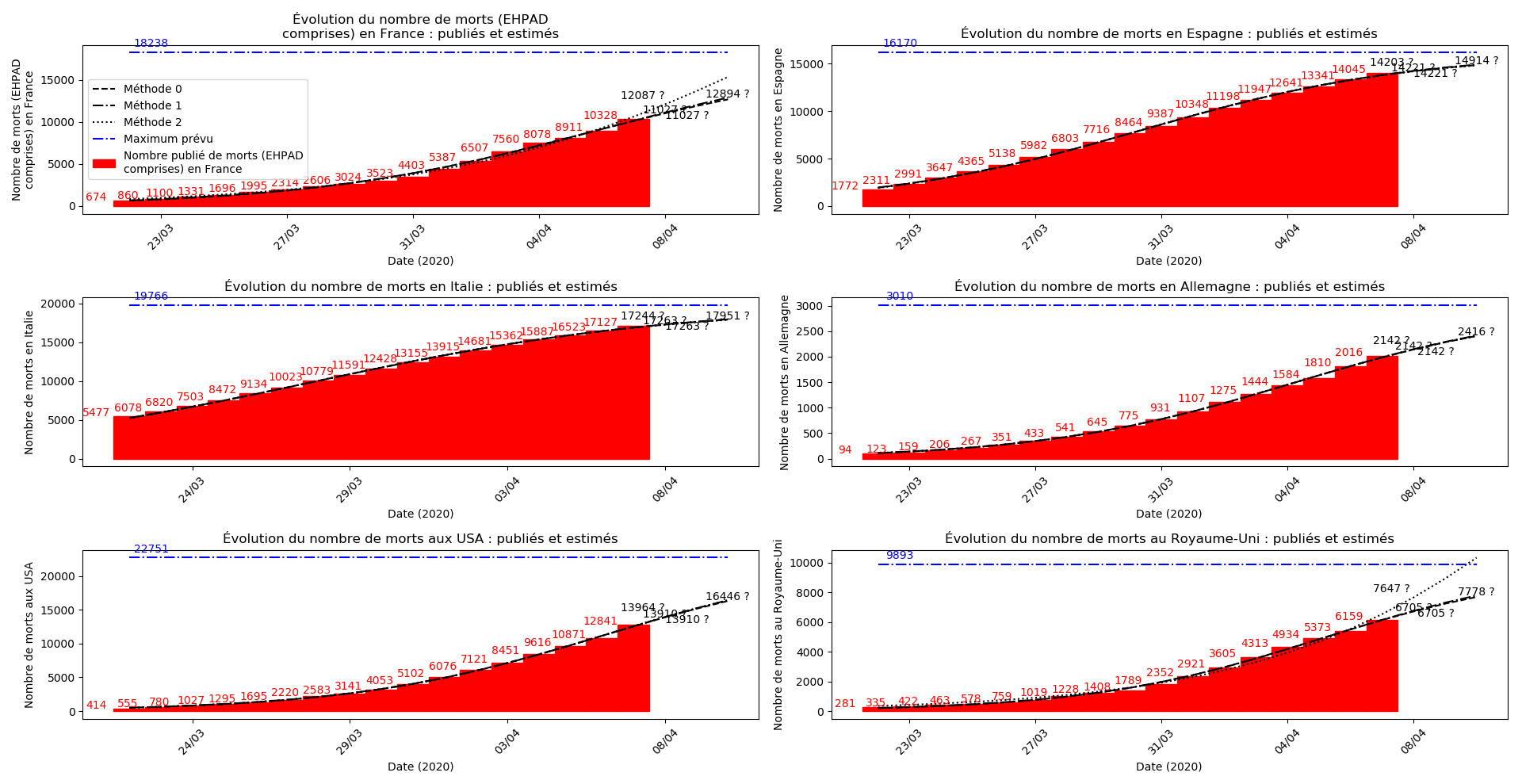
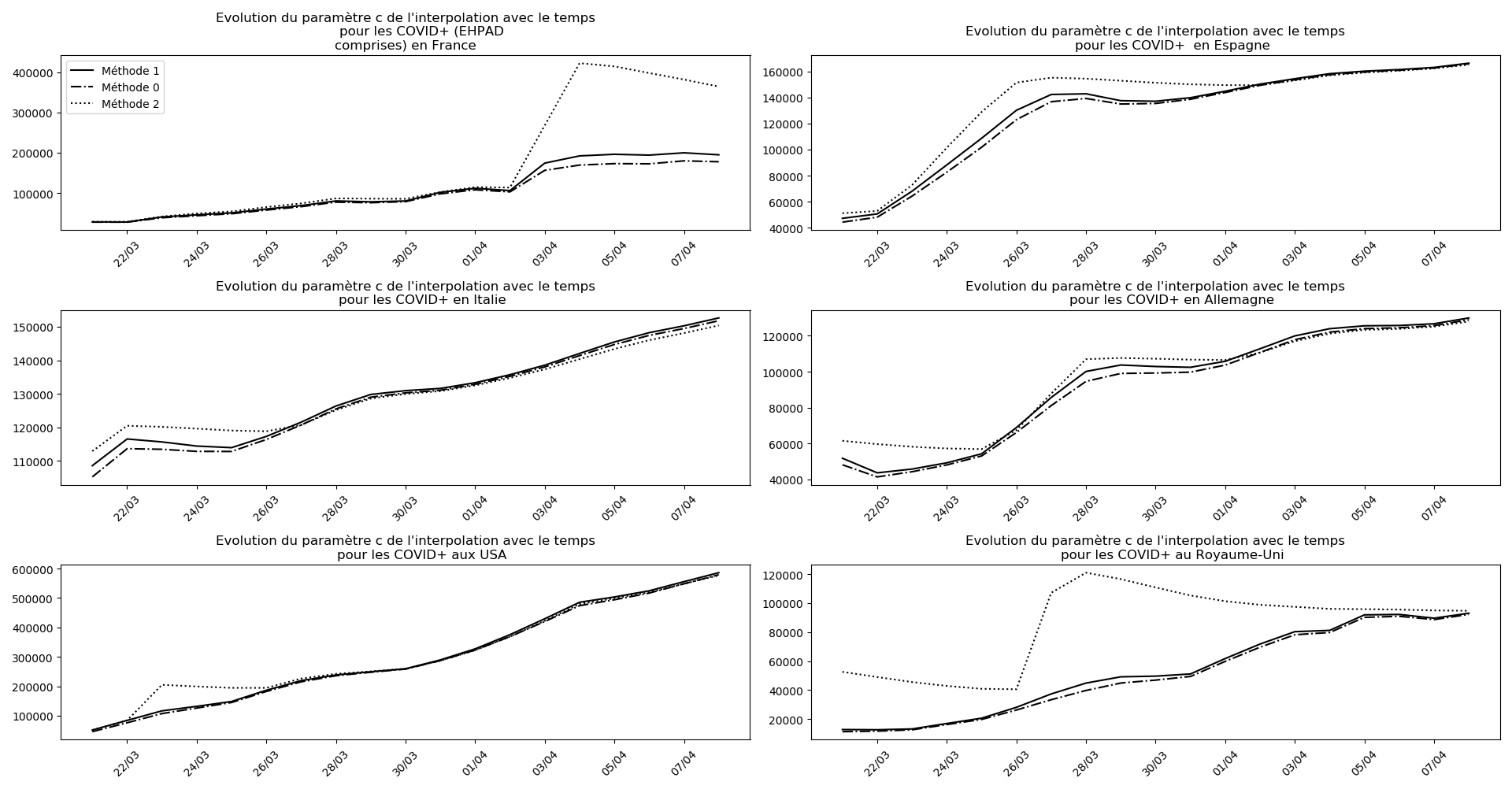
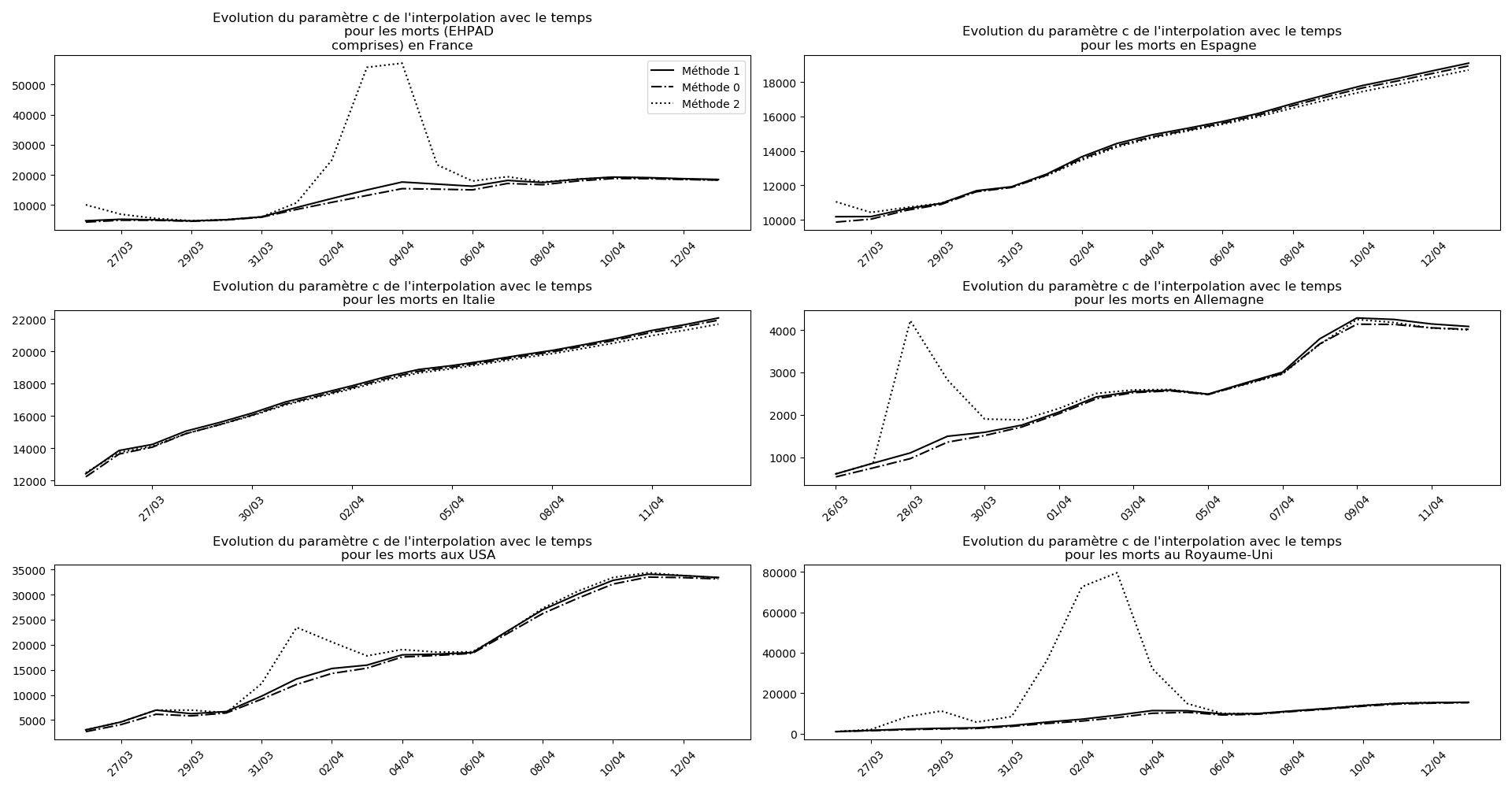
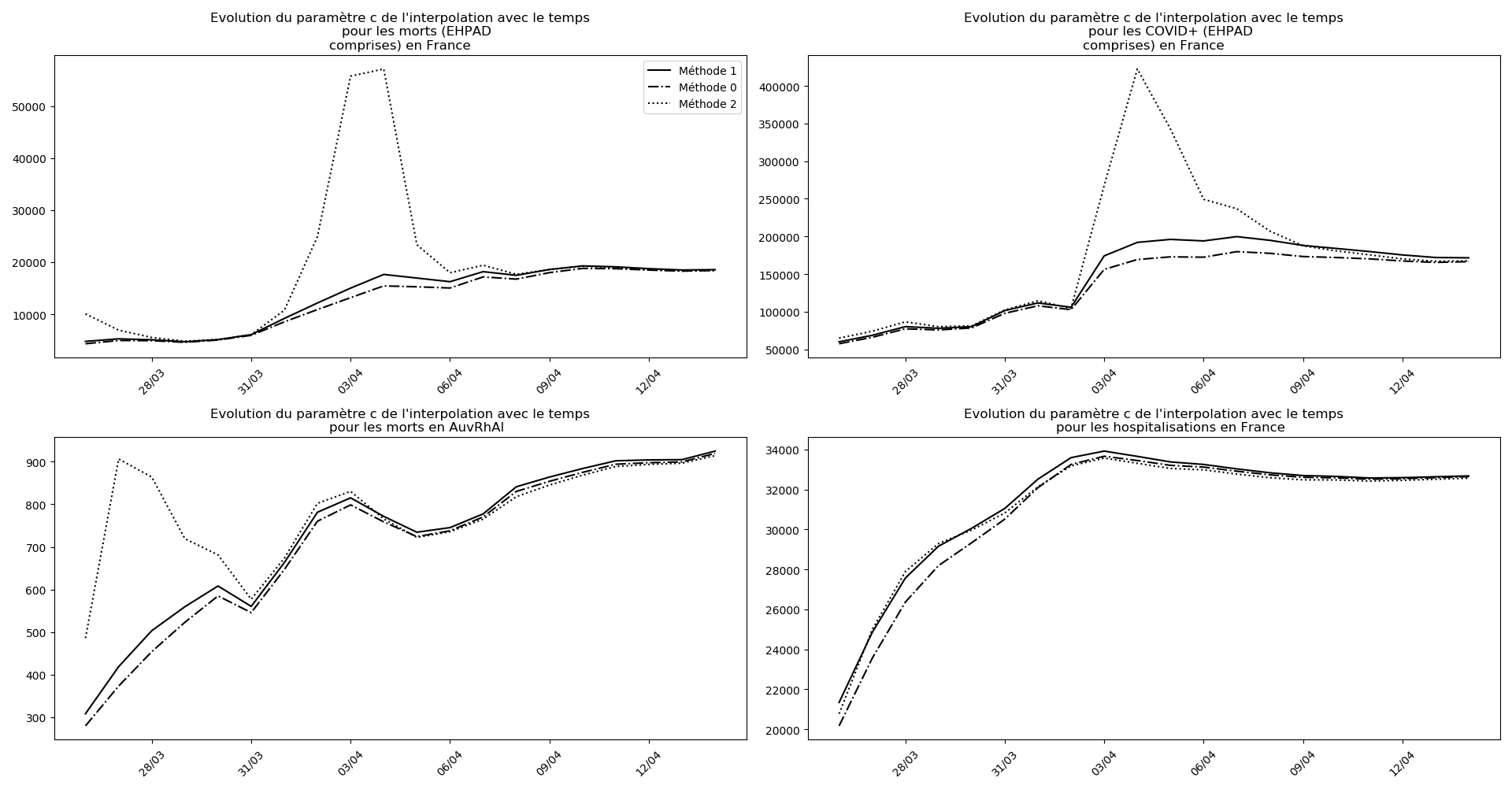
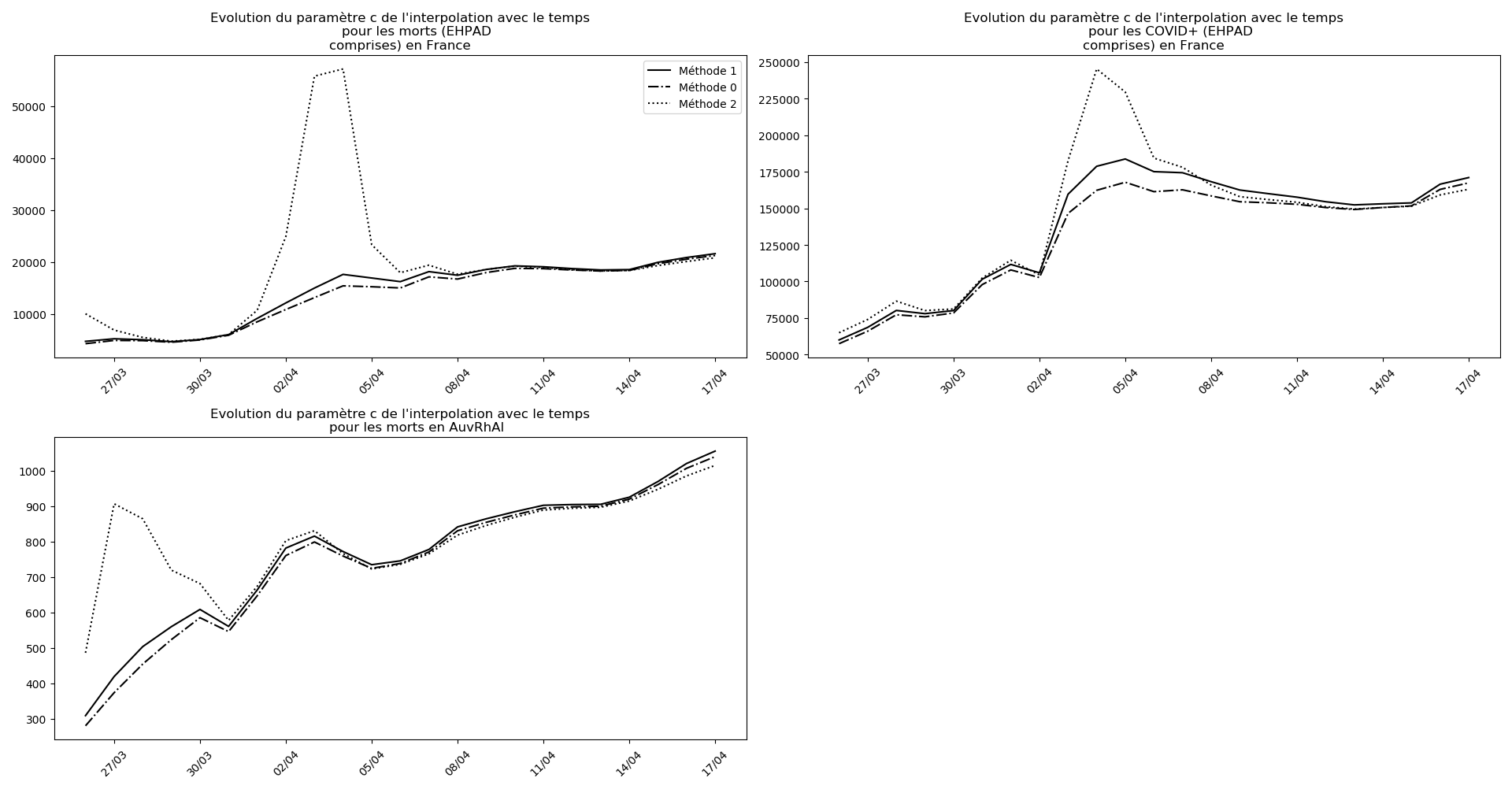
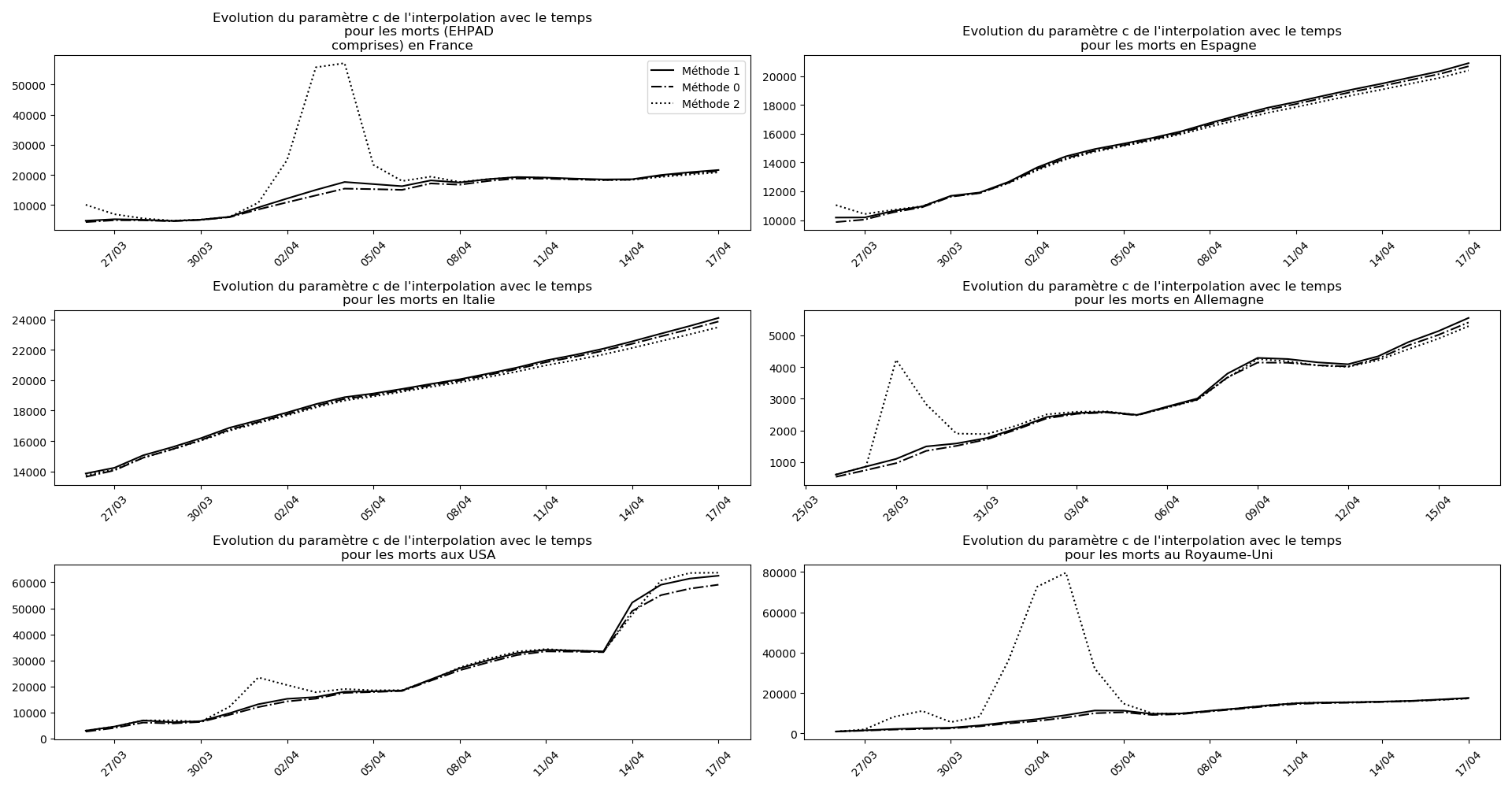
La brusque augmentation des données est brutalement prise en compte par la méthode 2 et je ne sais vraiment pas quel crédit on peut accorder aux prévisions qu’elle donne : aura-t-on vraiment plus de 50 000 morts en France en fin d’épidémie ?

Jusque-là, les trois méthodes donnaient aux alentours de 10 000 morts. Mais tous les décrochages de la méthode 2 se sont jusque-là révélés exacts : c’est en fait une des caractéristiques de cette méthode, c’est la seule qui se montre capable de prévoir très tôt le nombre asymptotique de cas en fin d’épidémie.

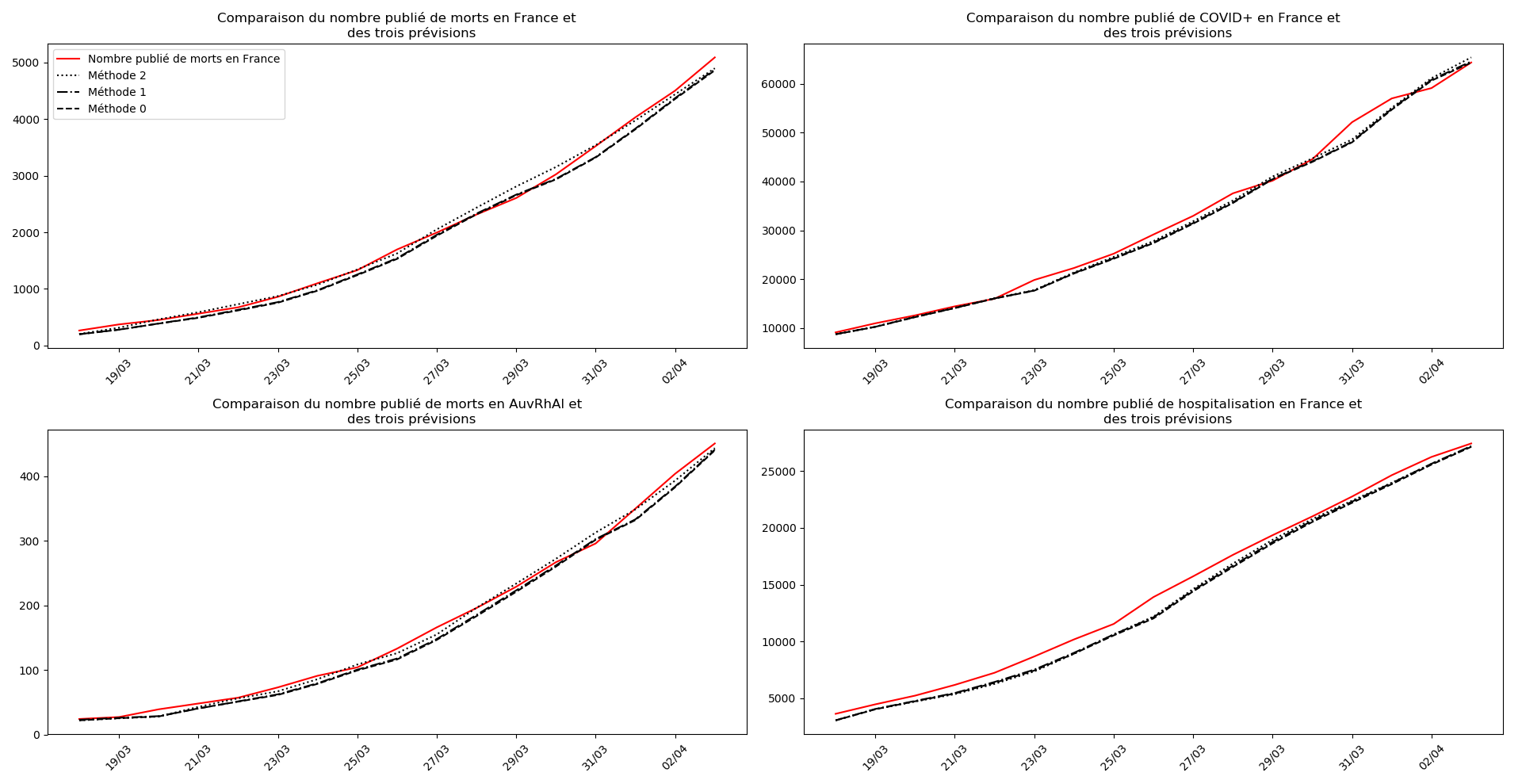
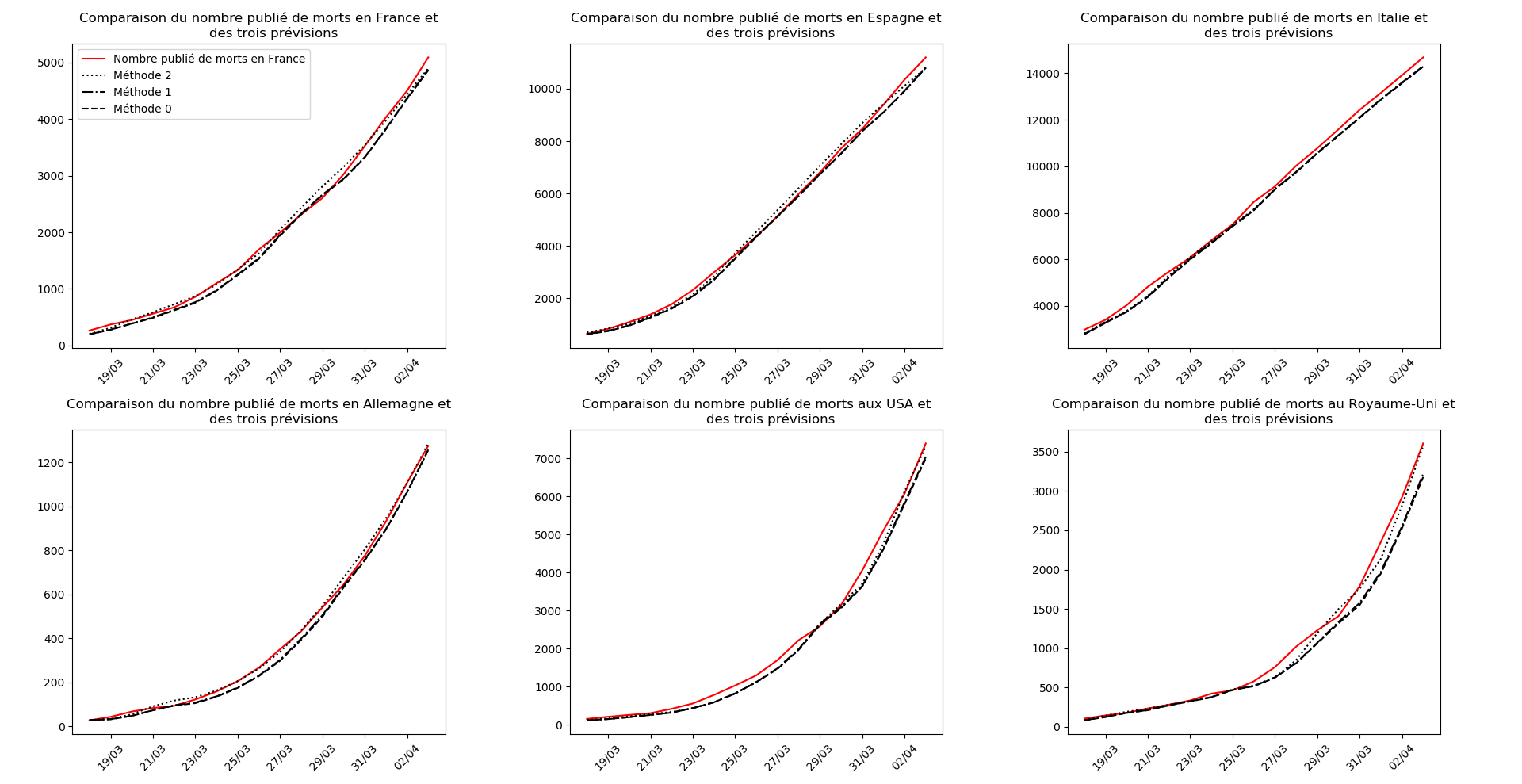
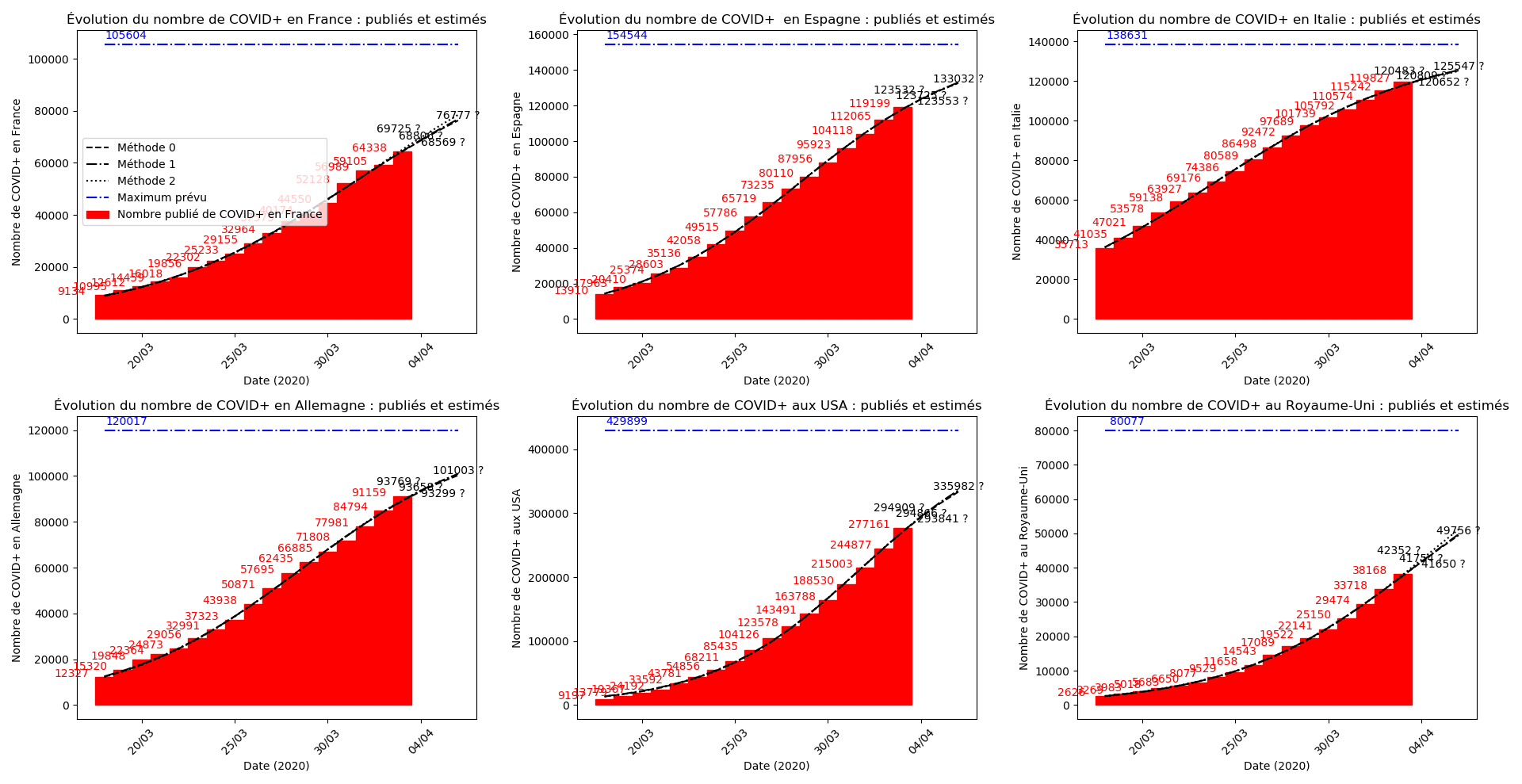
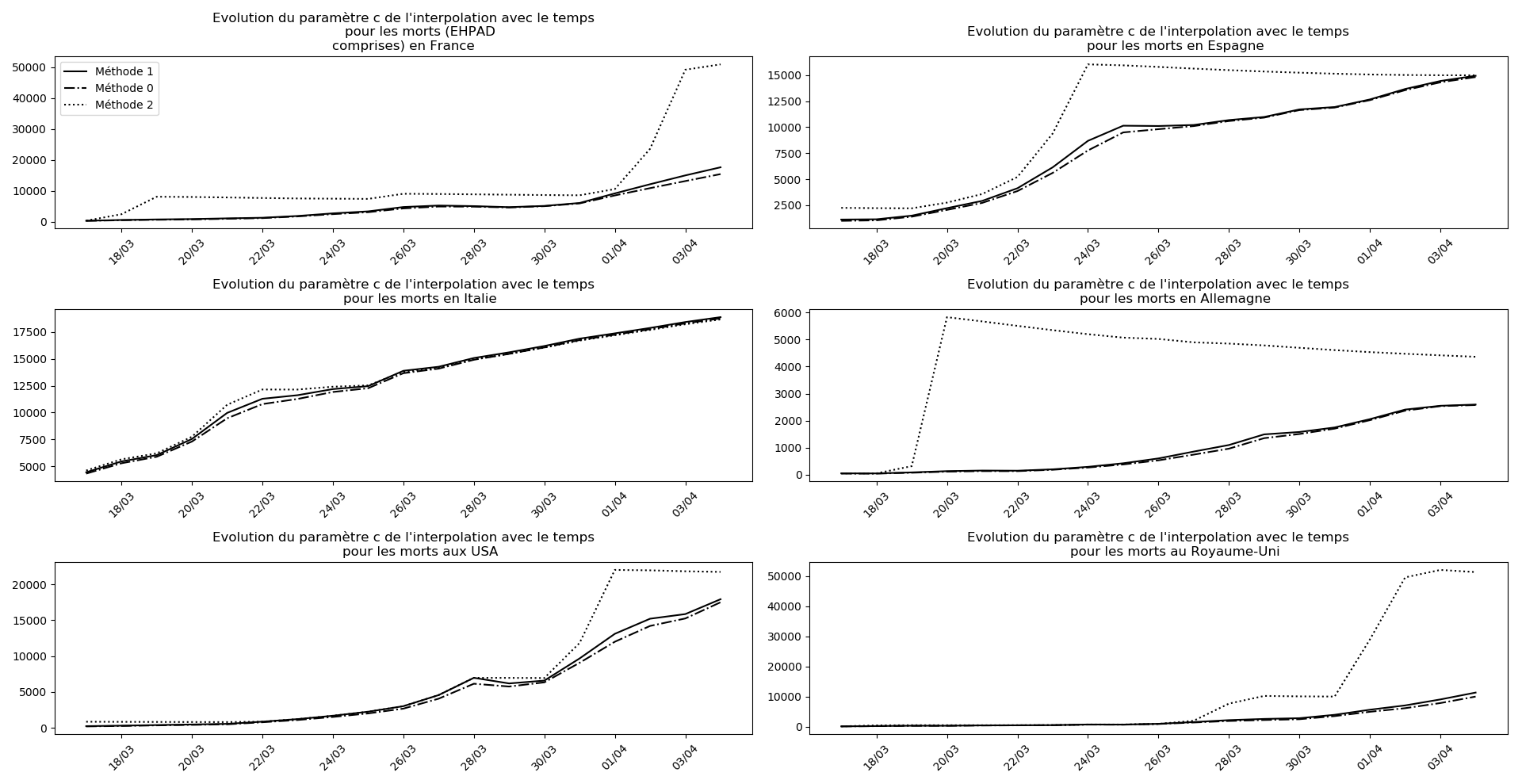
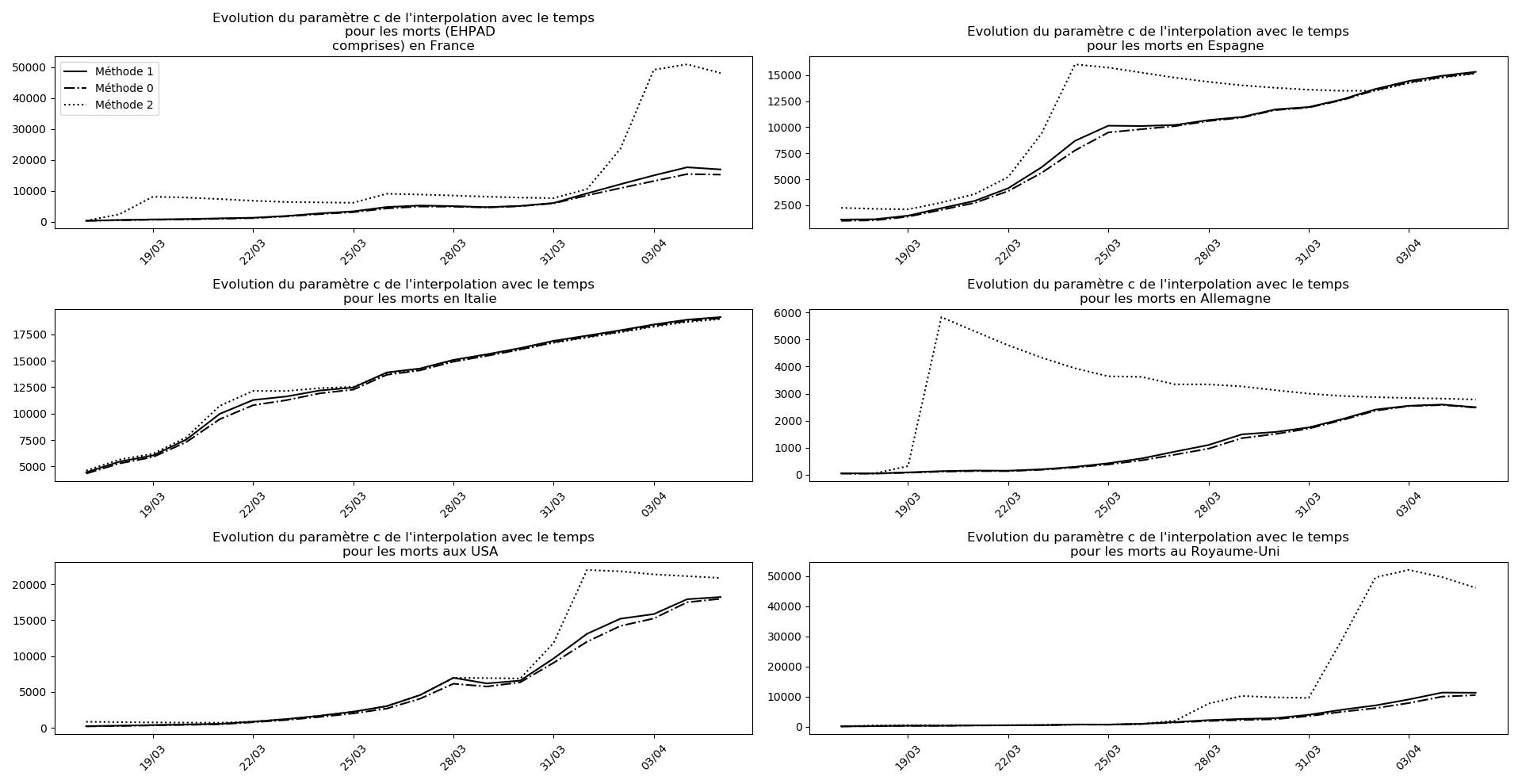
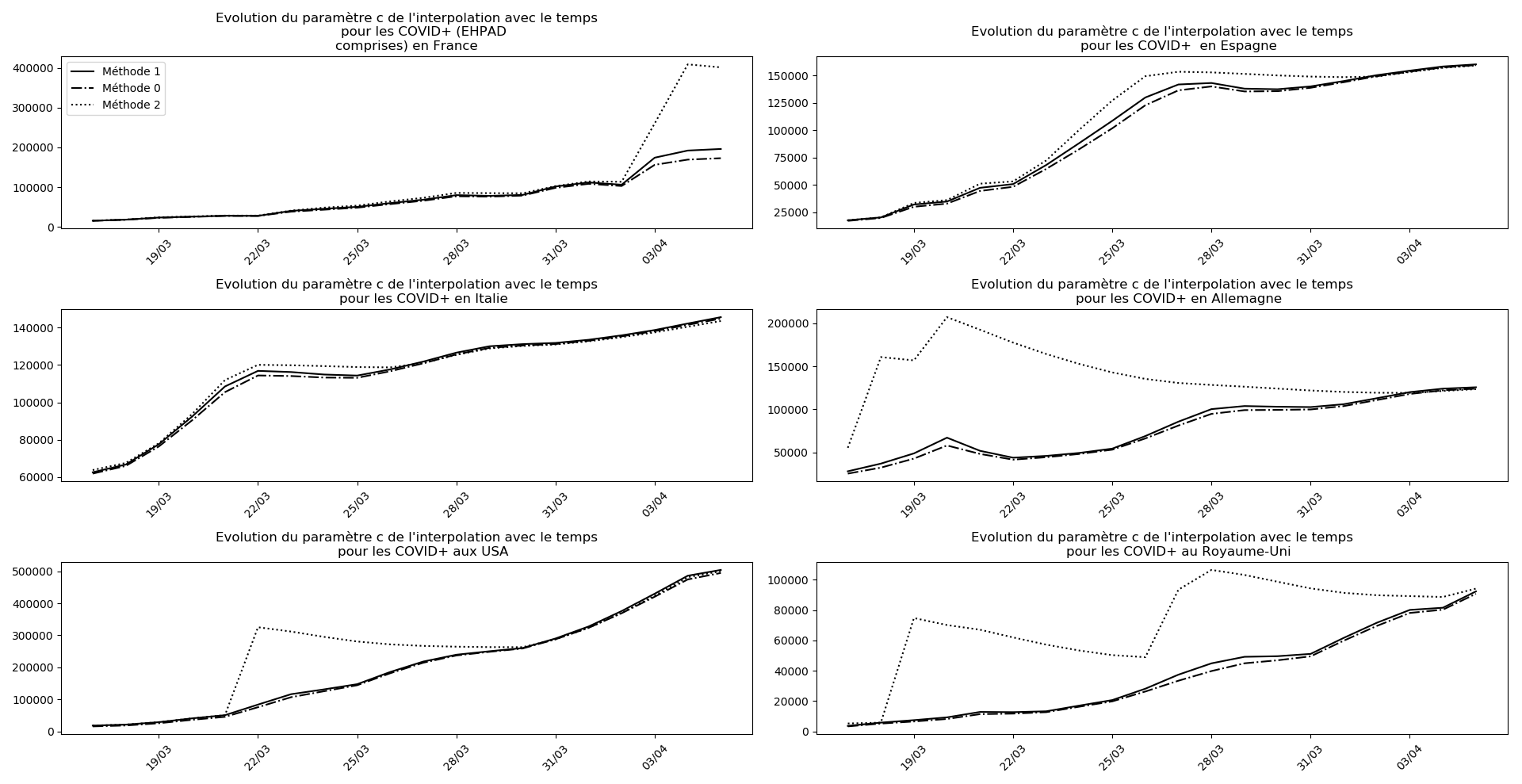
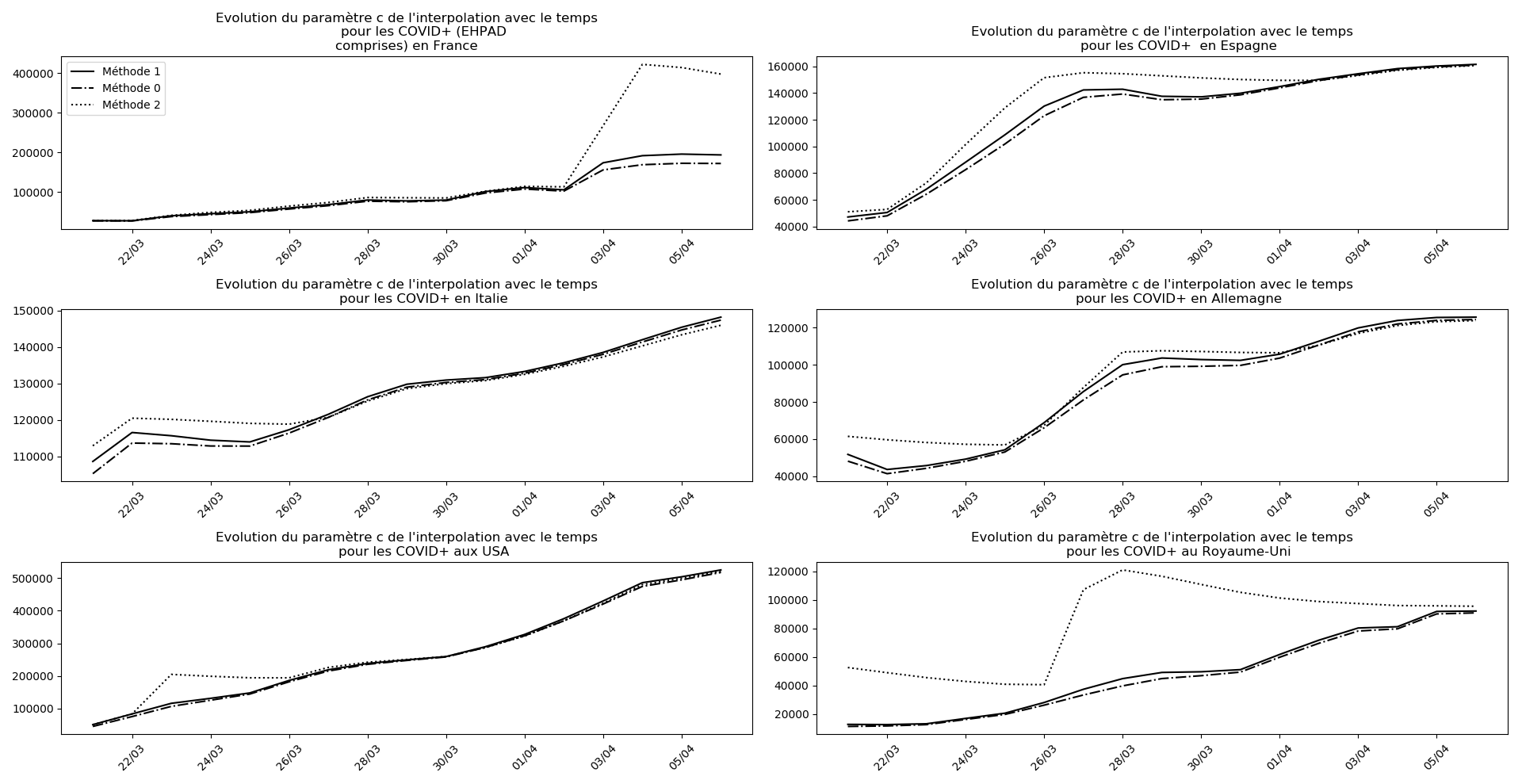
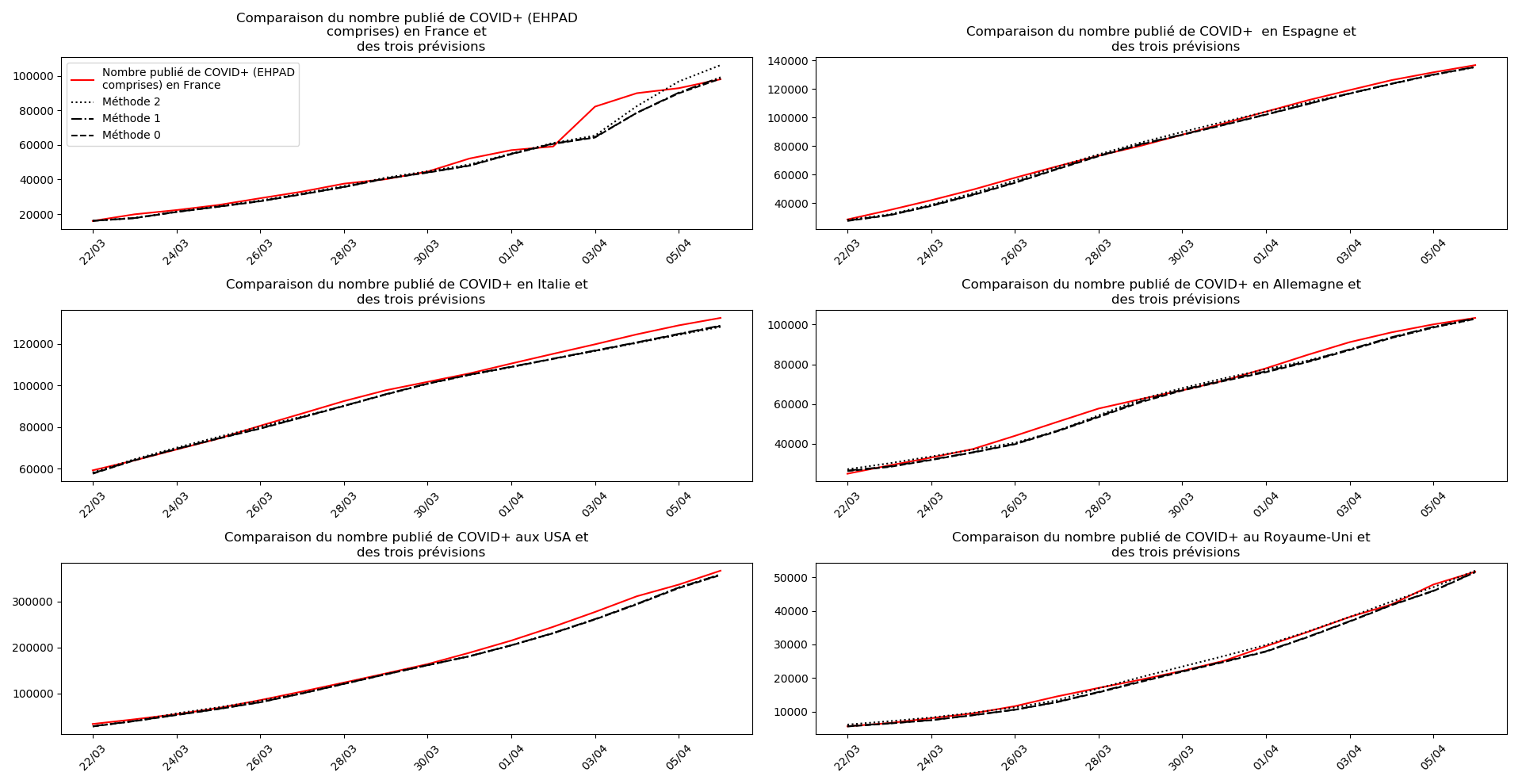
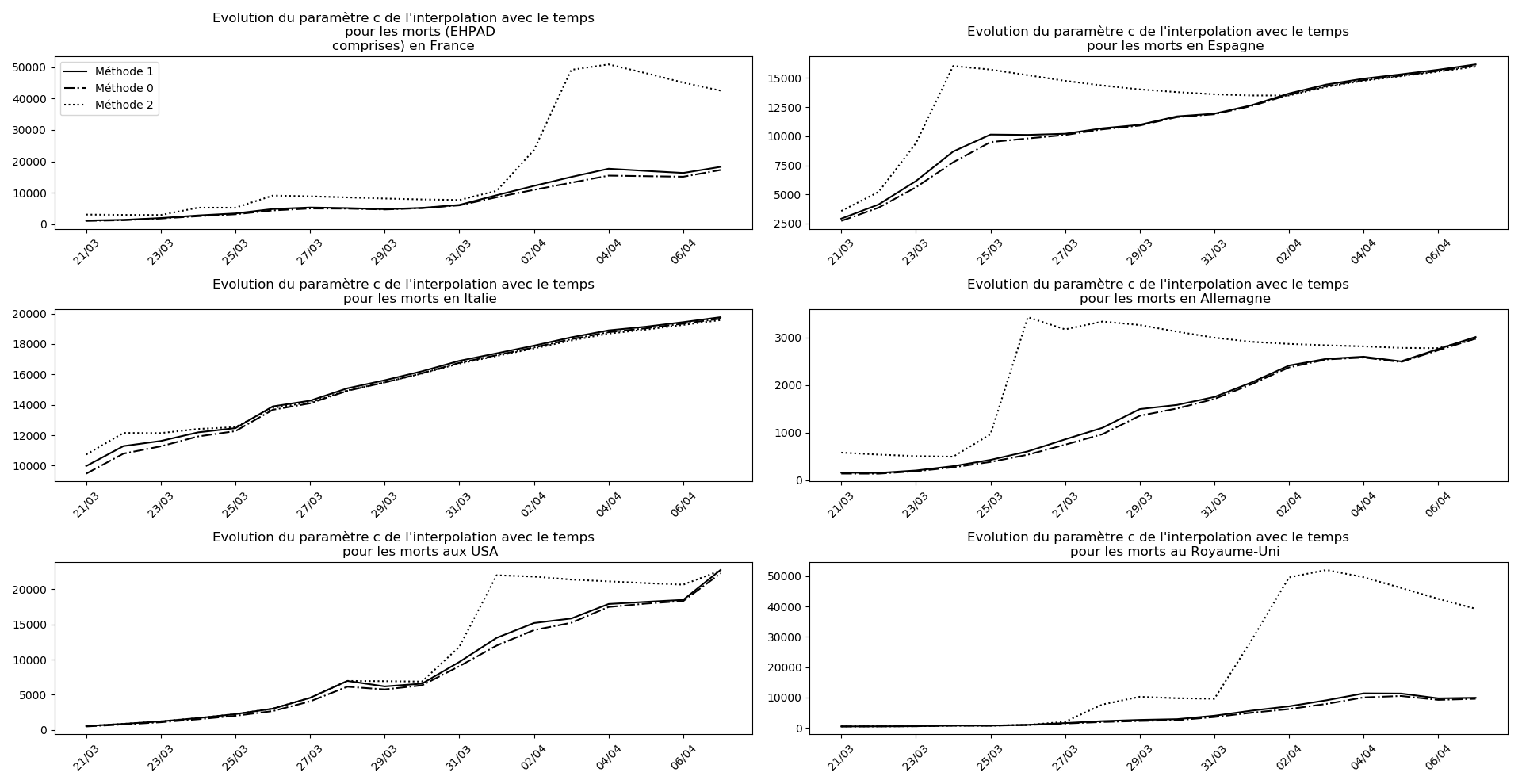
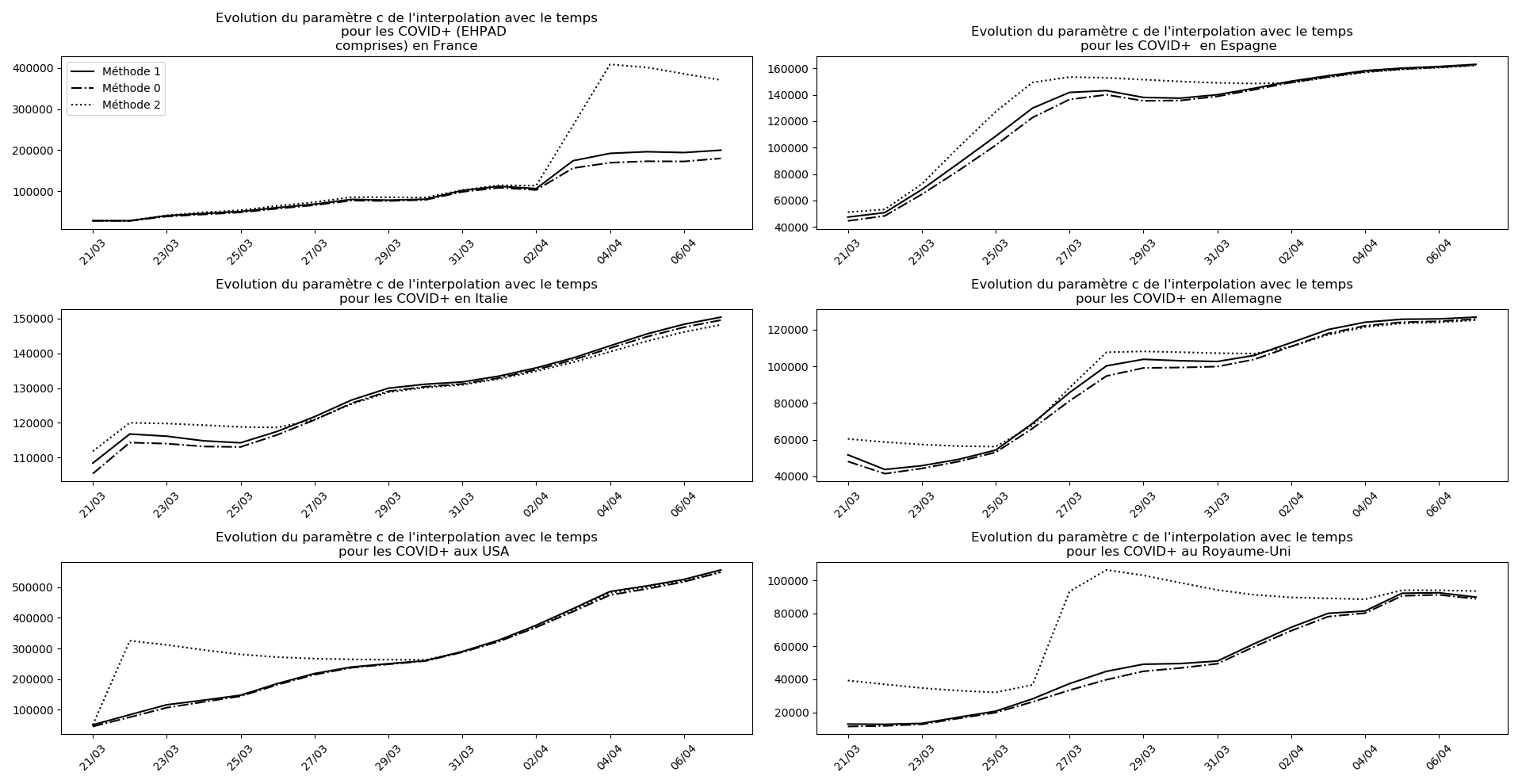
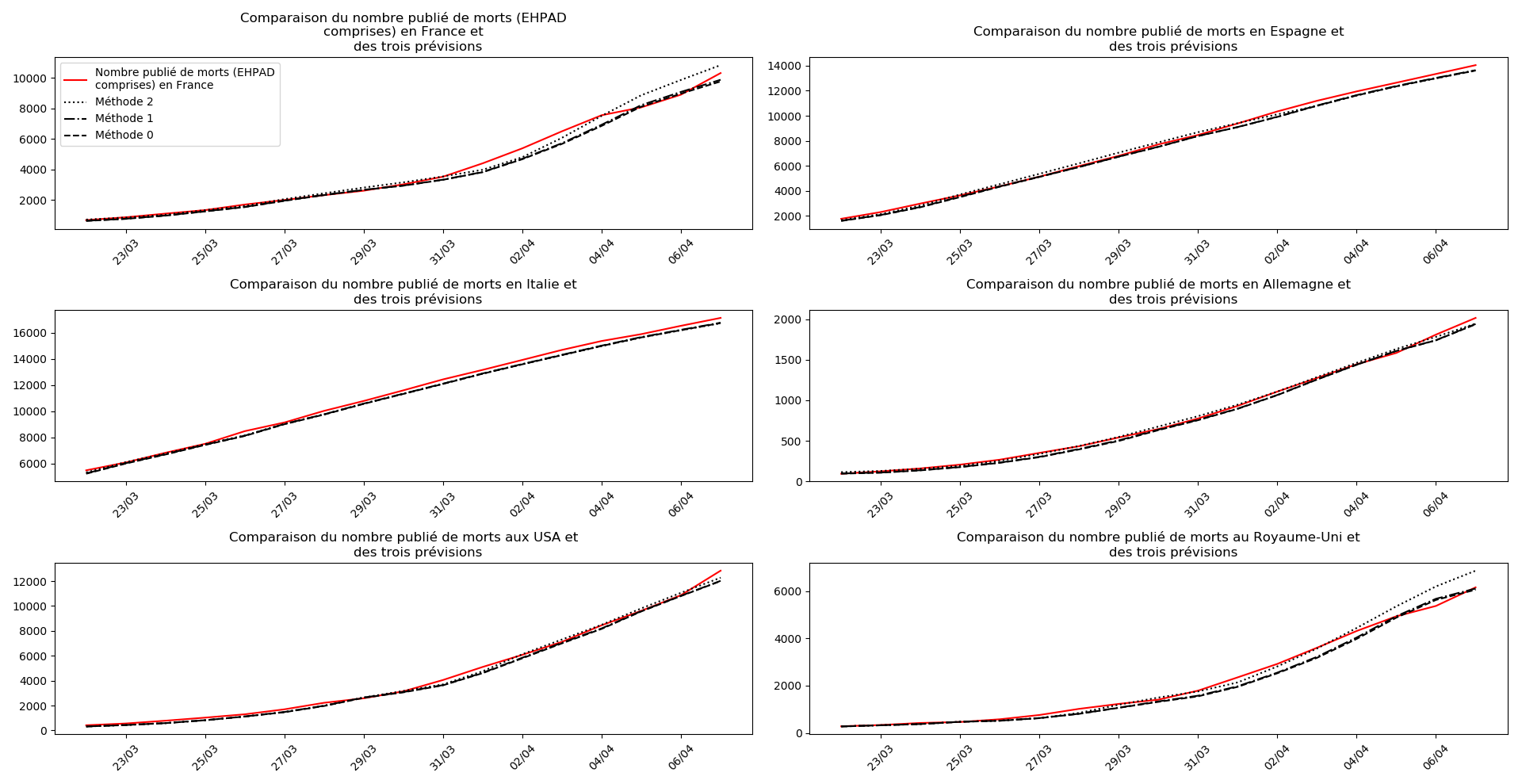
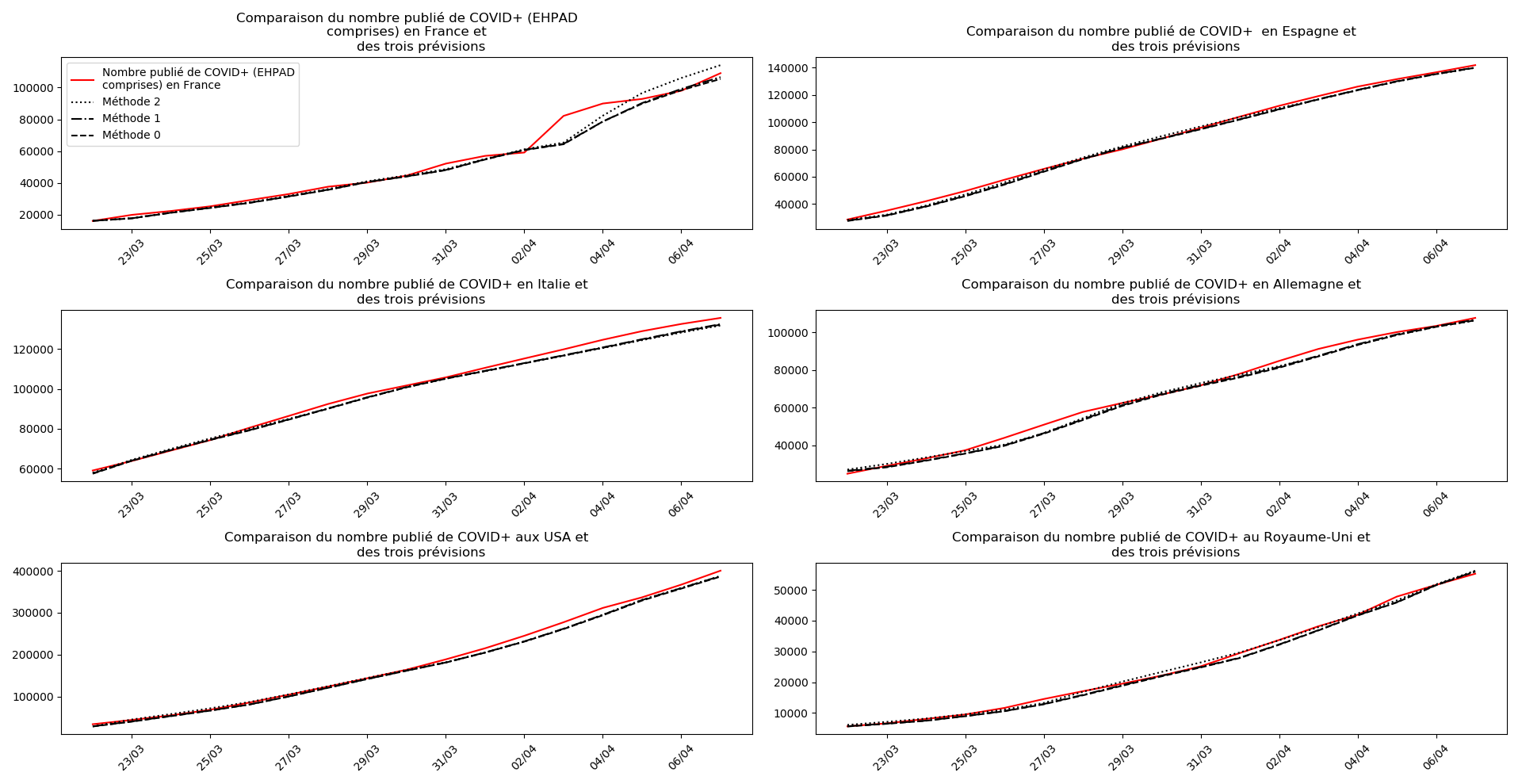
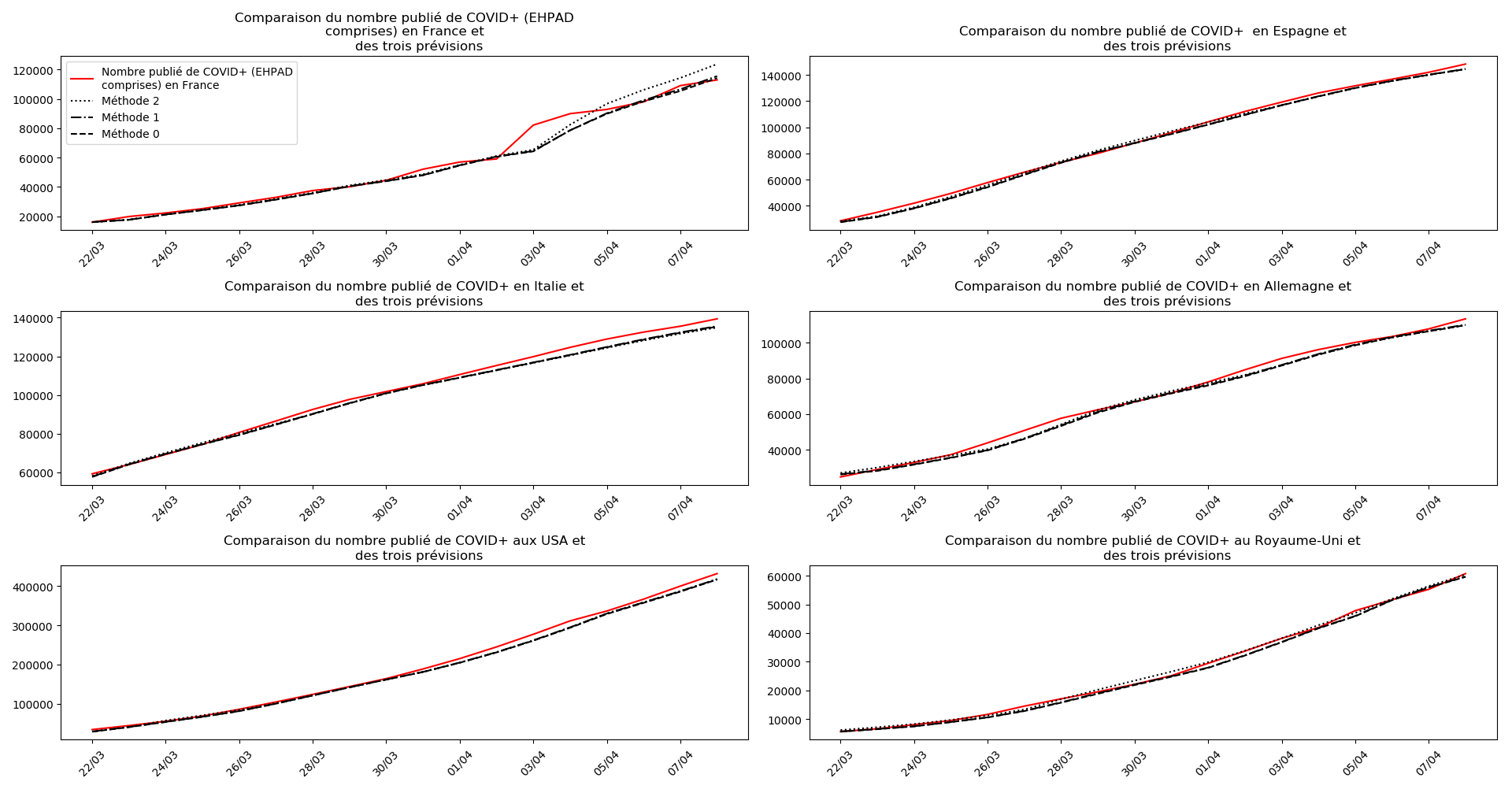
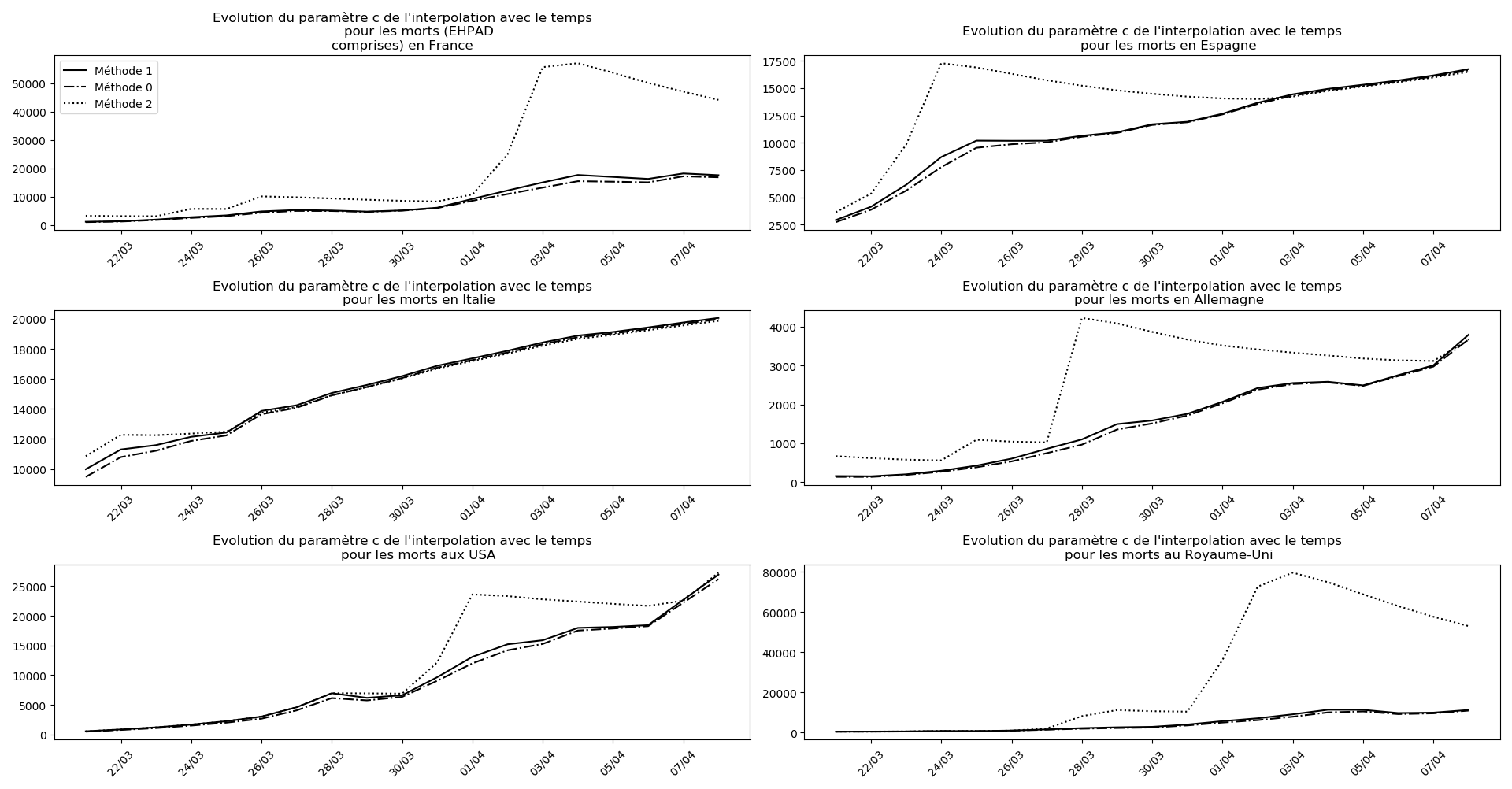
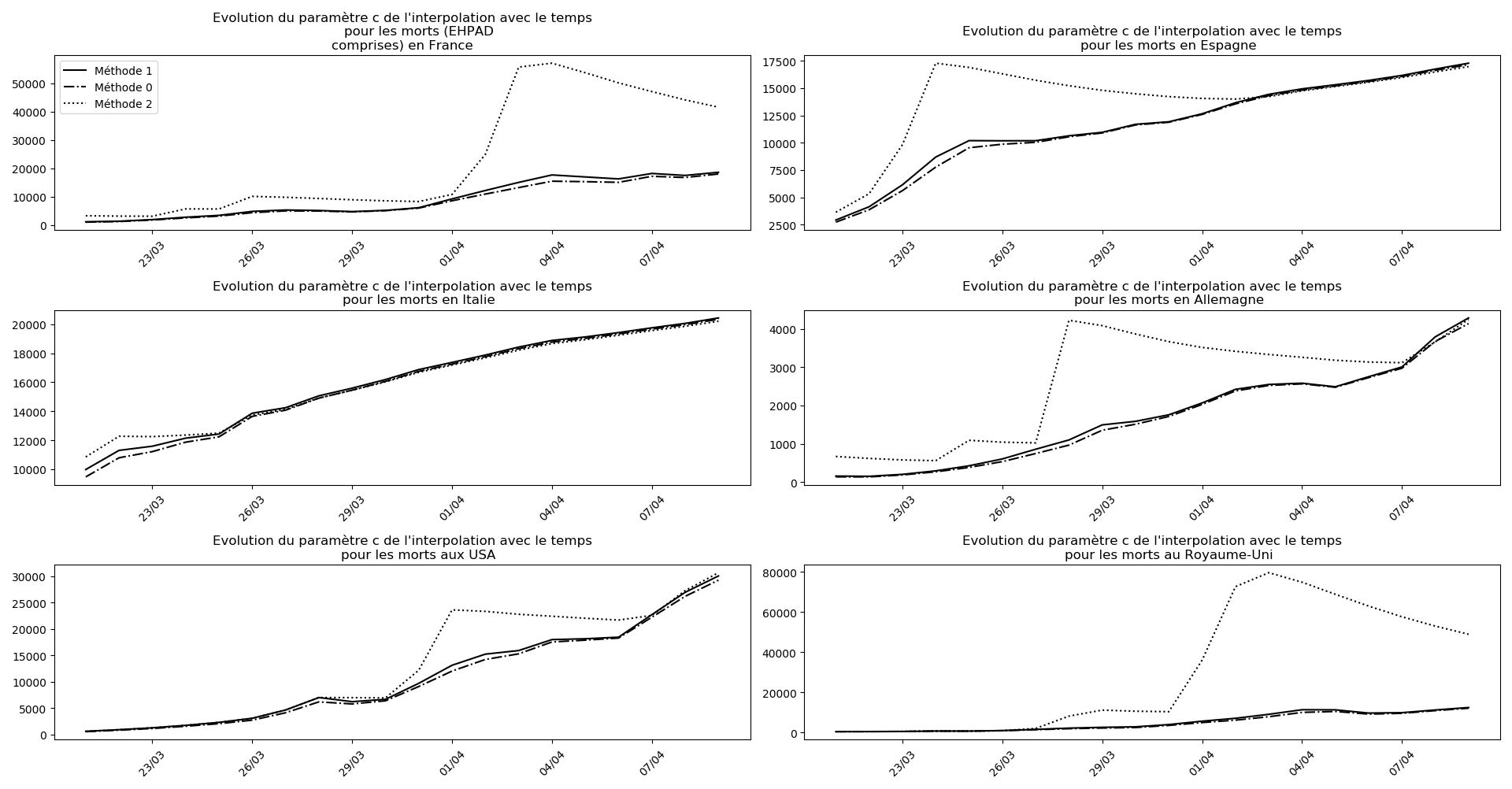
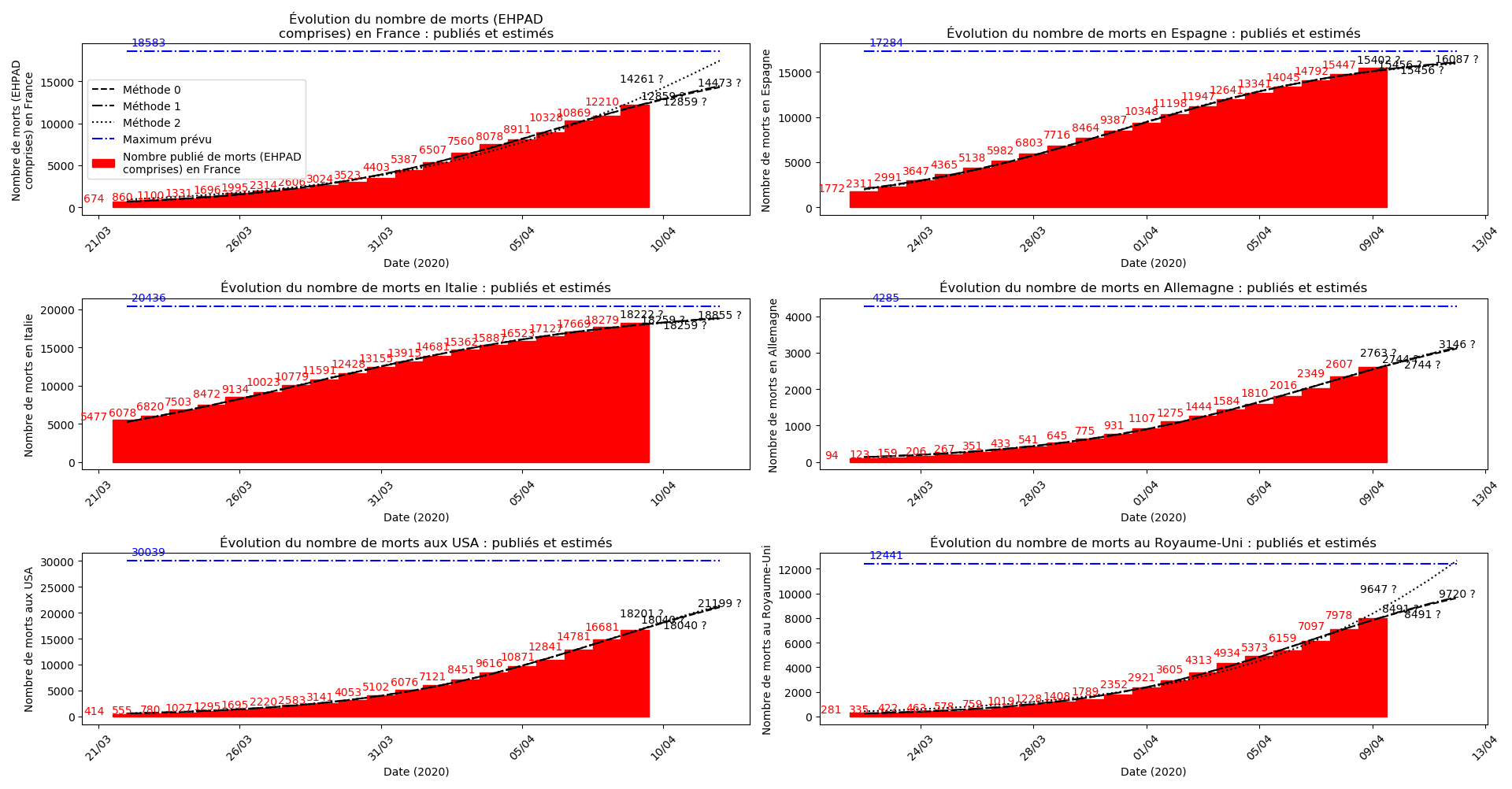
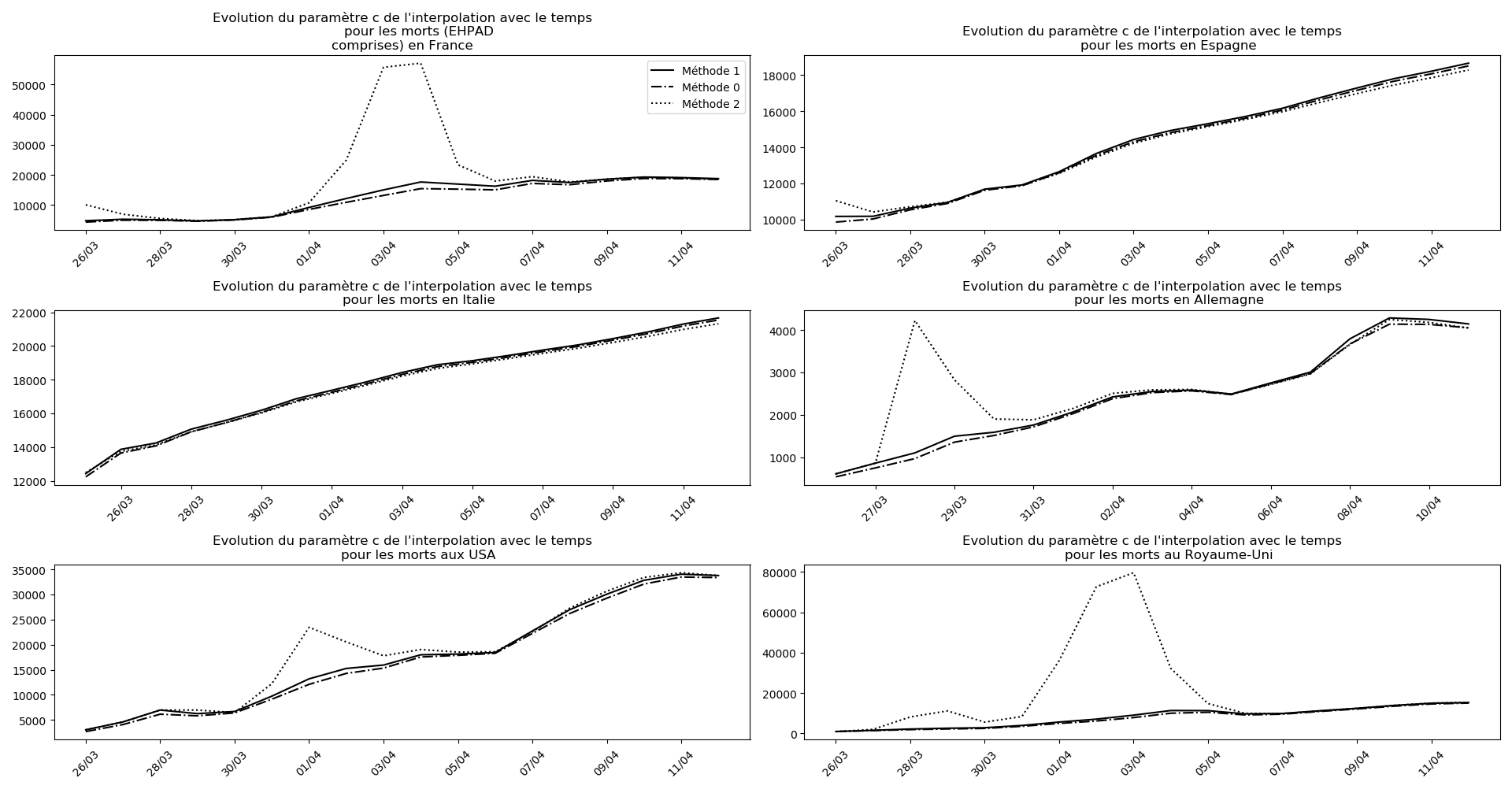
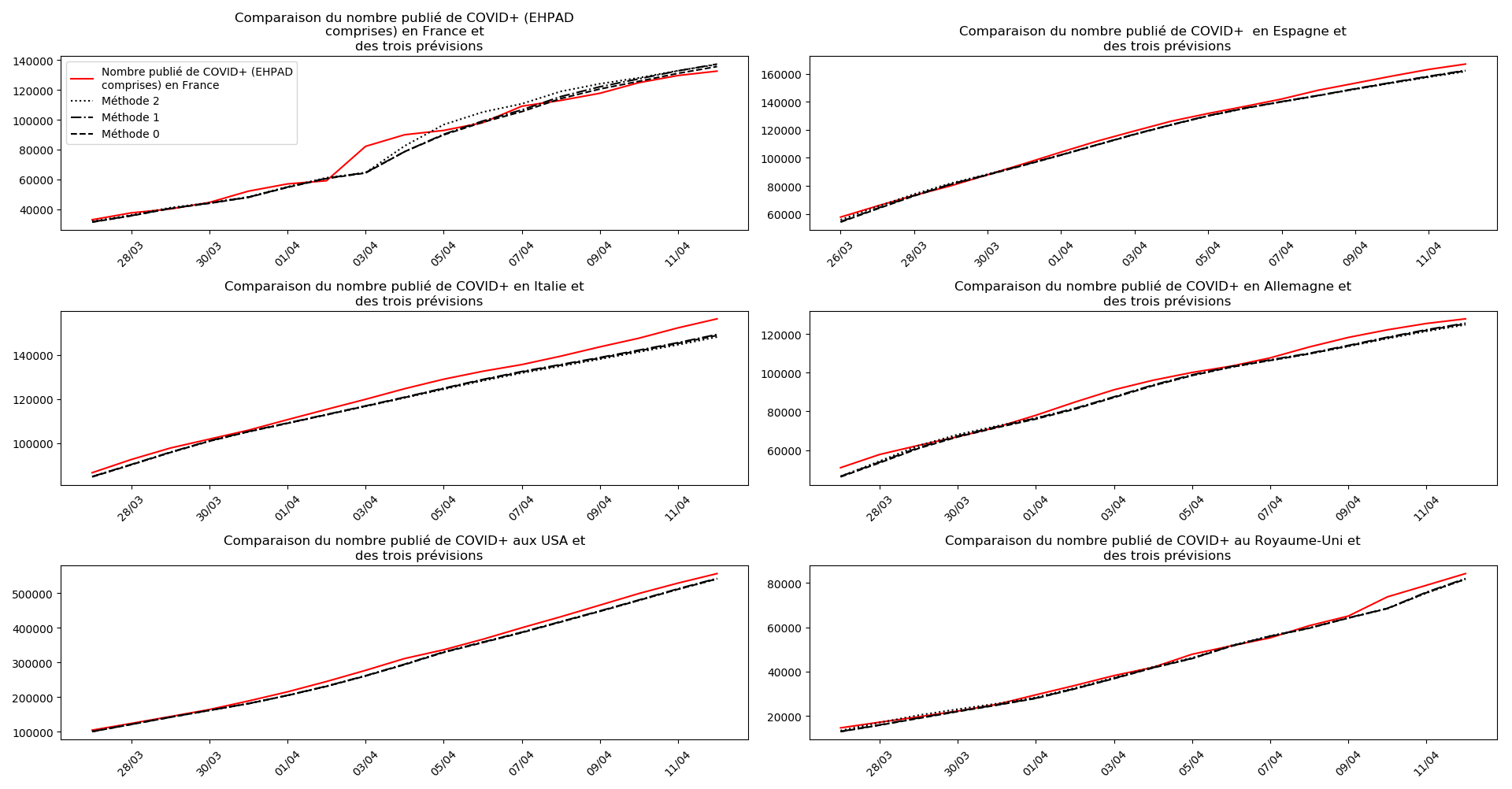
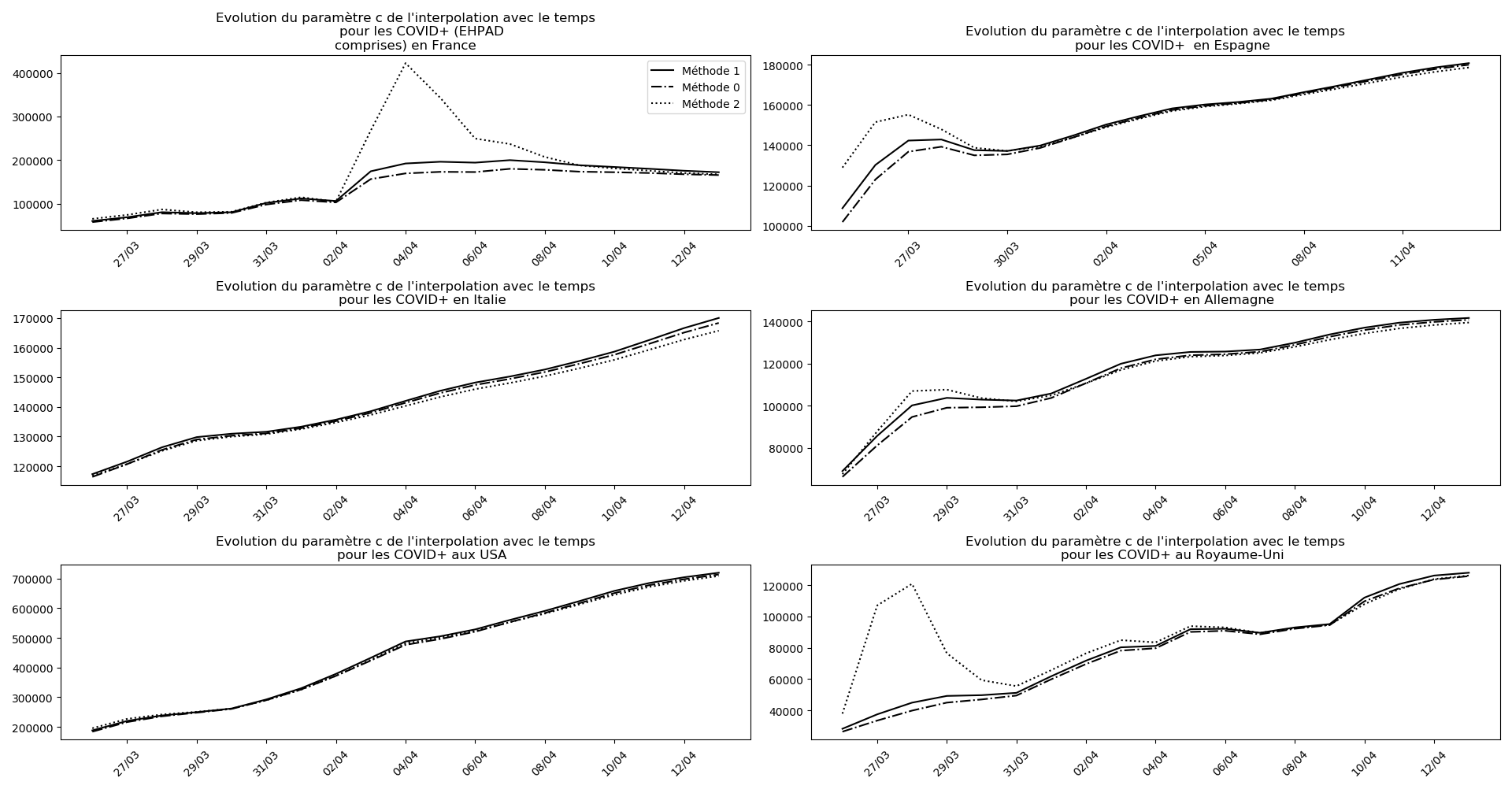
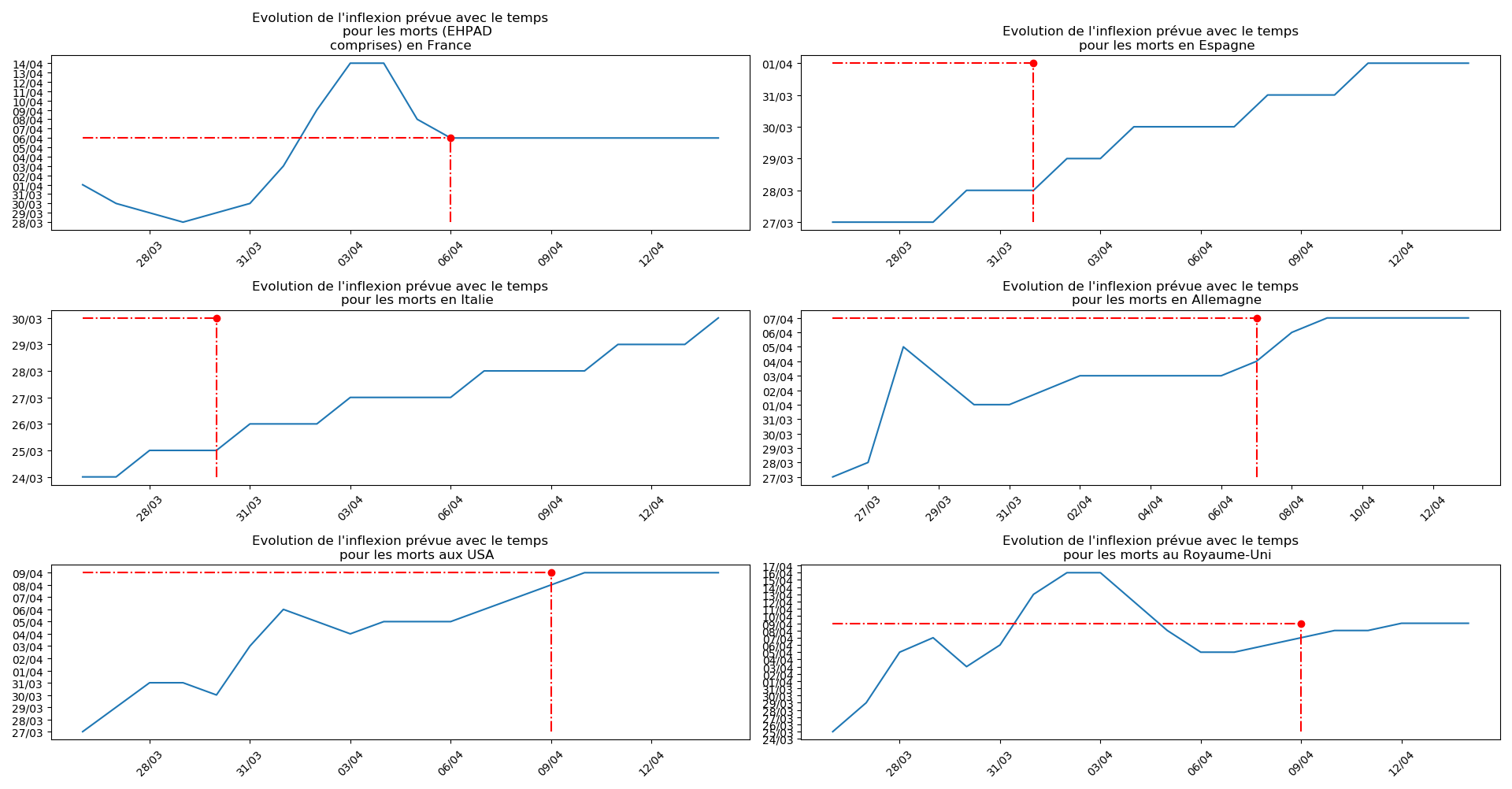
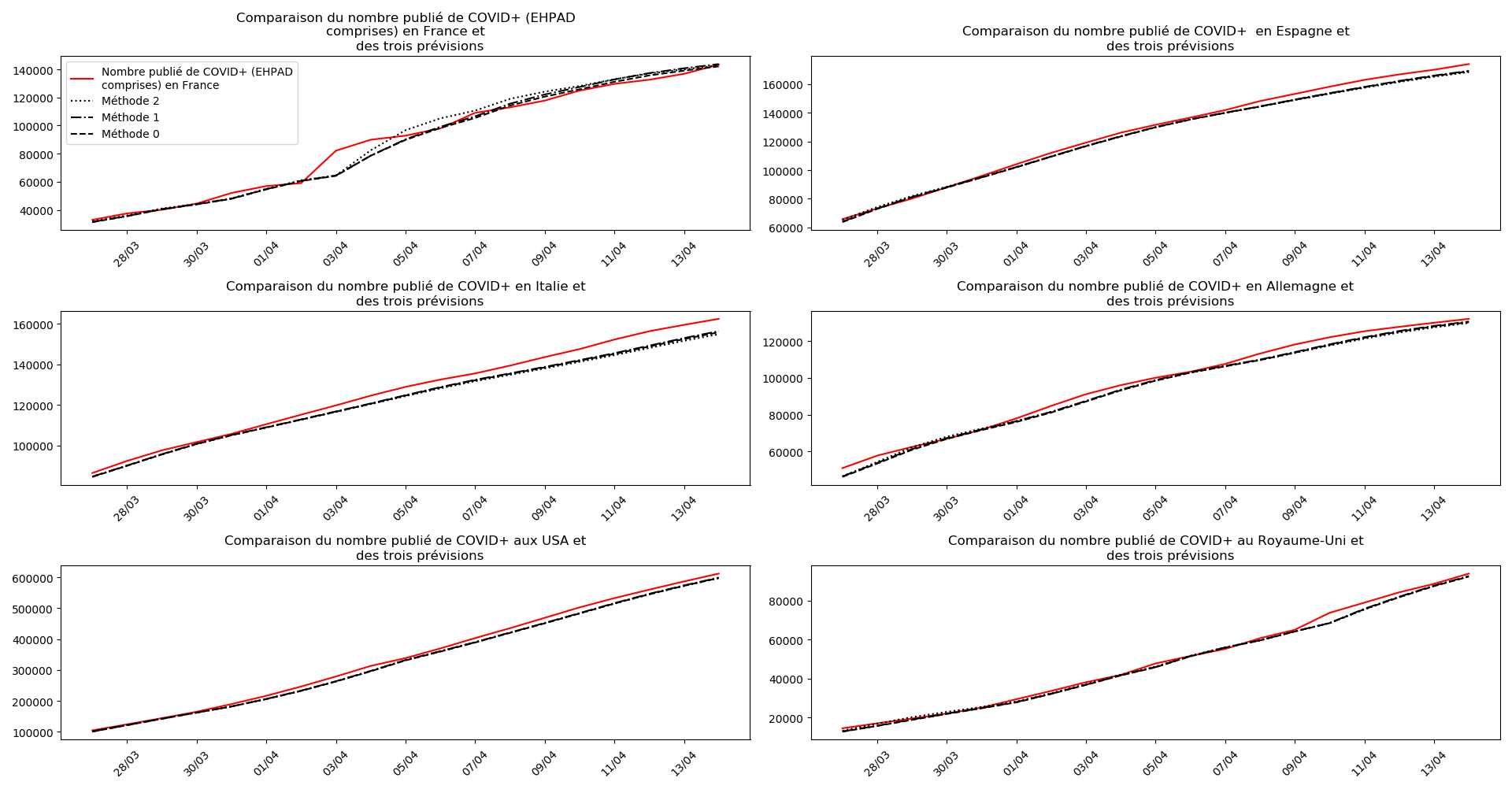
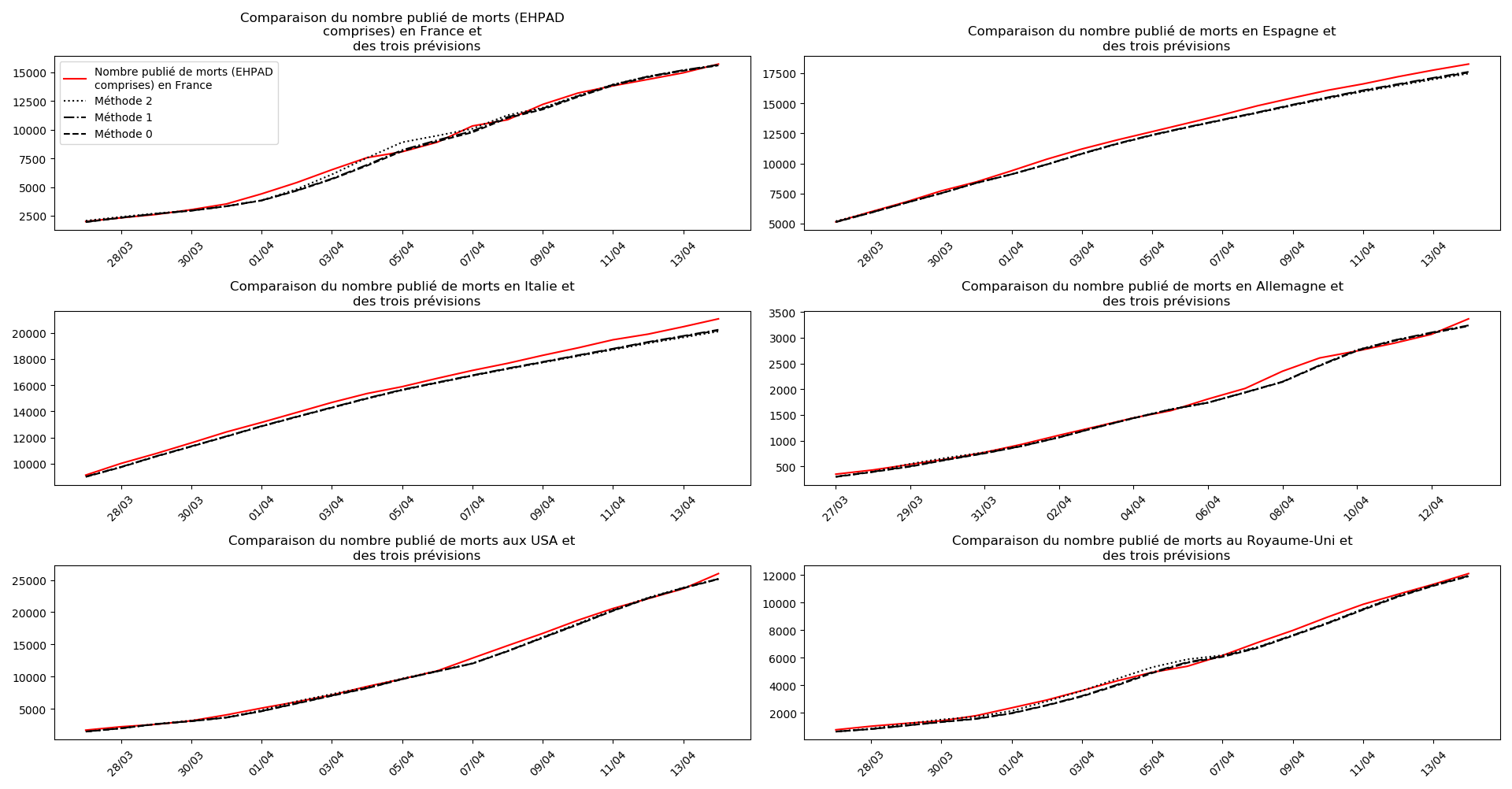
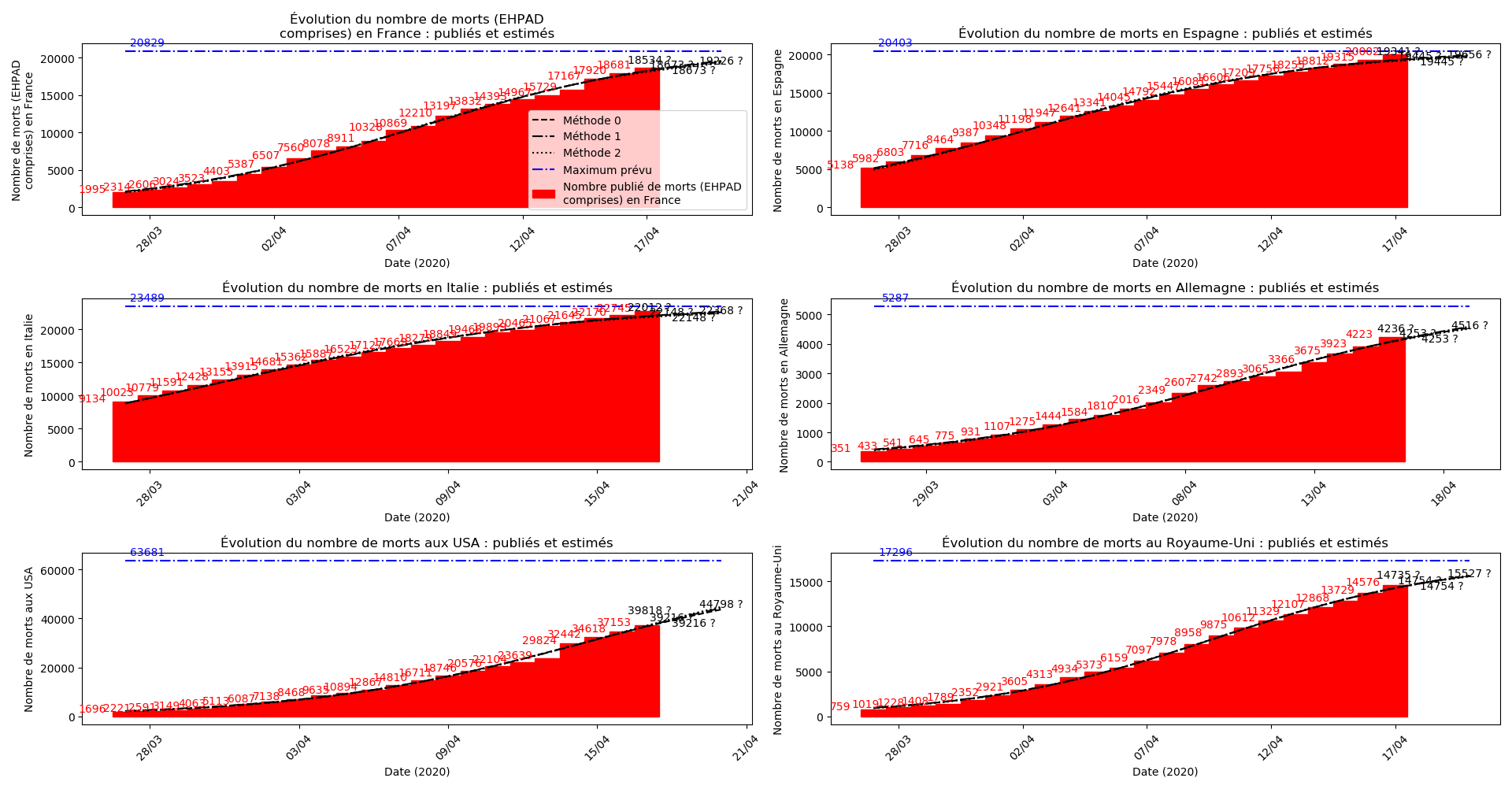
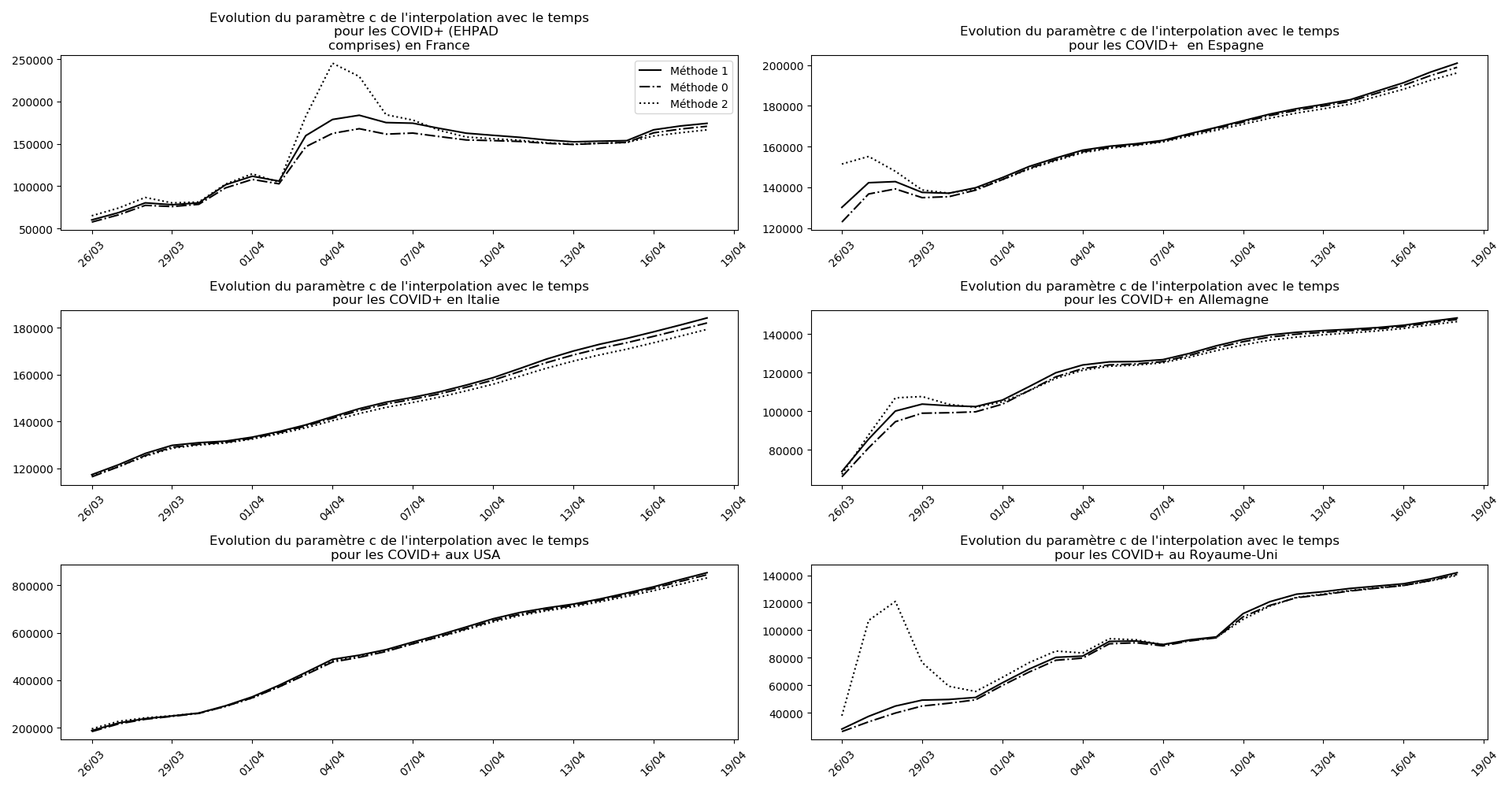
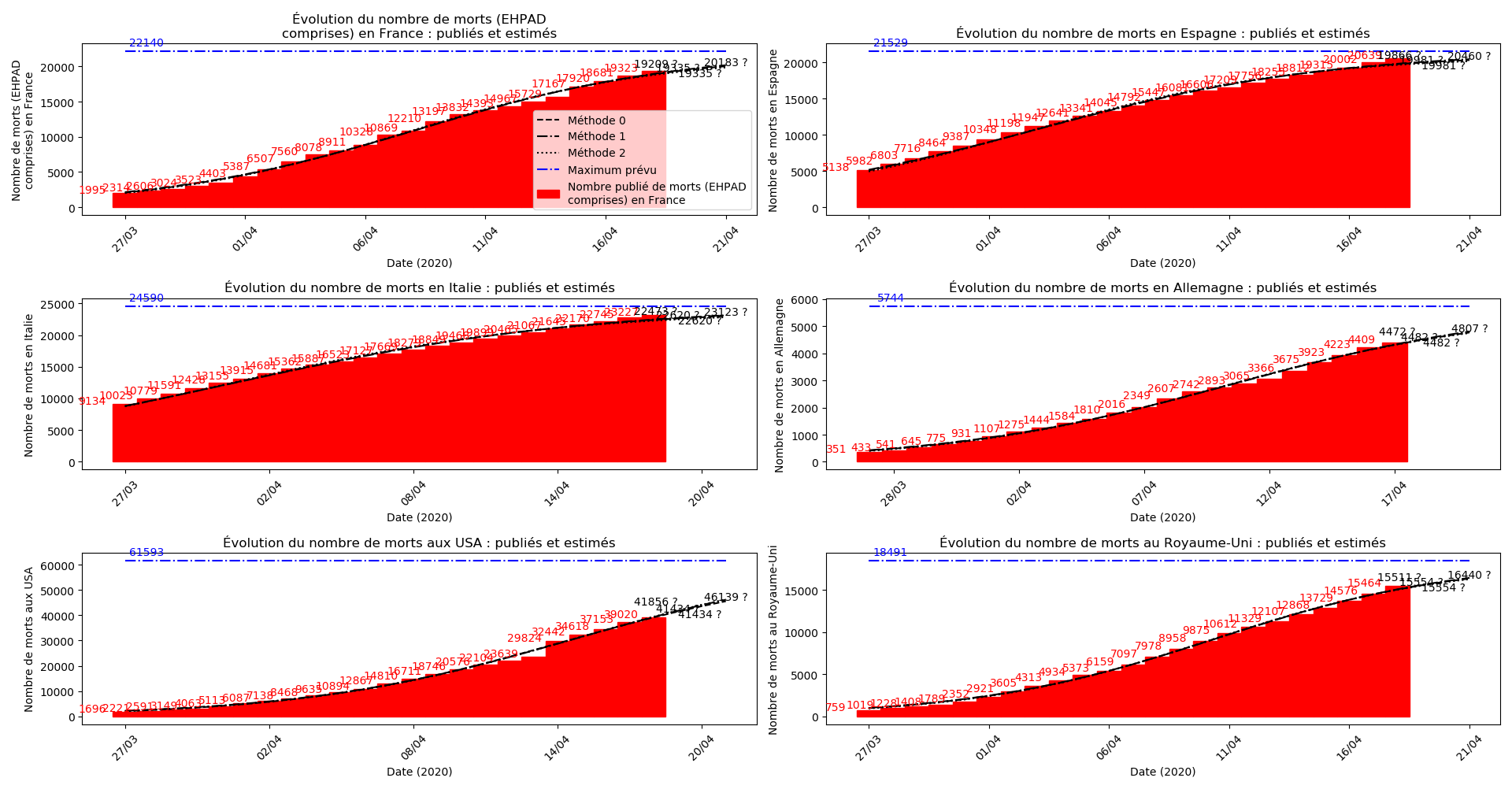
Voici par exemple ce que donnent les trois méthodes pour la France, l’Espagne, l’Italie, l’Allemagne, les USA et le Royaume-Uni :

Comme on peut le voir sur les cas de l’Espagne, de l’Allemagne, des USA et du Royaume-Uni, les décrochages précoces de la méthode 2 se trouvent plus tard confirmés par les deux autres méthodes.

Concernant le cas particulier de la France et des deux dénombrements distincts EHPAD/hors EHPAD, il y a quand même lieu de douter de la validité des prévisions obtenues. Et il faut espérer qu’elles soient fausses…

Mais en dehors des difficultés purement algorithmiques, cela pose aussi des questions beaucoup plus politiques et morales :

Pourquoi avoir fait deux dénombrements séparés ? Pourquoi continuer à présenter les morts en EHPAD à côté de ceux hors EHPAD (ici par exemple) ? Est-ce que les morts en EHPAD ne sont pas de véritables morts ?
Faut-il comprendre que les malades en EHPAD n’ont pas le droit à une hospitalisation ? Il n’y a pas à ma connaissance de décomptes séparés des hospitalisations venant d’EHPAD et des autres, ou des réanimations en EHPAD et des réanimations en hôpital.
Les EHPAD disposent-elles d’ailleurs de lits de réanimation ? J’en doute fortement…
@EPhilippePM@twitter.com et @olivierveran@twitter.com ont publié un décret permettant de prescrire, jusqu’au 15 avril 2020, de manière dérogatoire, du Rivotril - je cite - “en vue de la prise en charge des patients atteints ou susceptibles d’être atteints par le virus SARS-CoV-2”. Sachant que ce médicament est fortement contre-indiqué en cas d’insuffisance pulmonaire, il y a lieu de se demander si les malades en EHPAD n’ont pas tout simplement été sacrifiés par le gouvernement français, conscient que les hôpitaux français, dans lesquels plus de 60000 lits ont été fermés ces 10 dernières années, ne pourraient pas prendre en charge l’ensemble de la population atteinte…
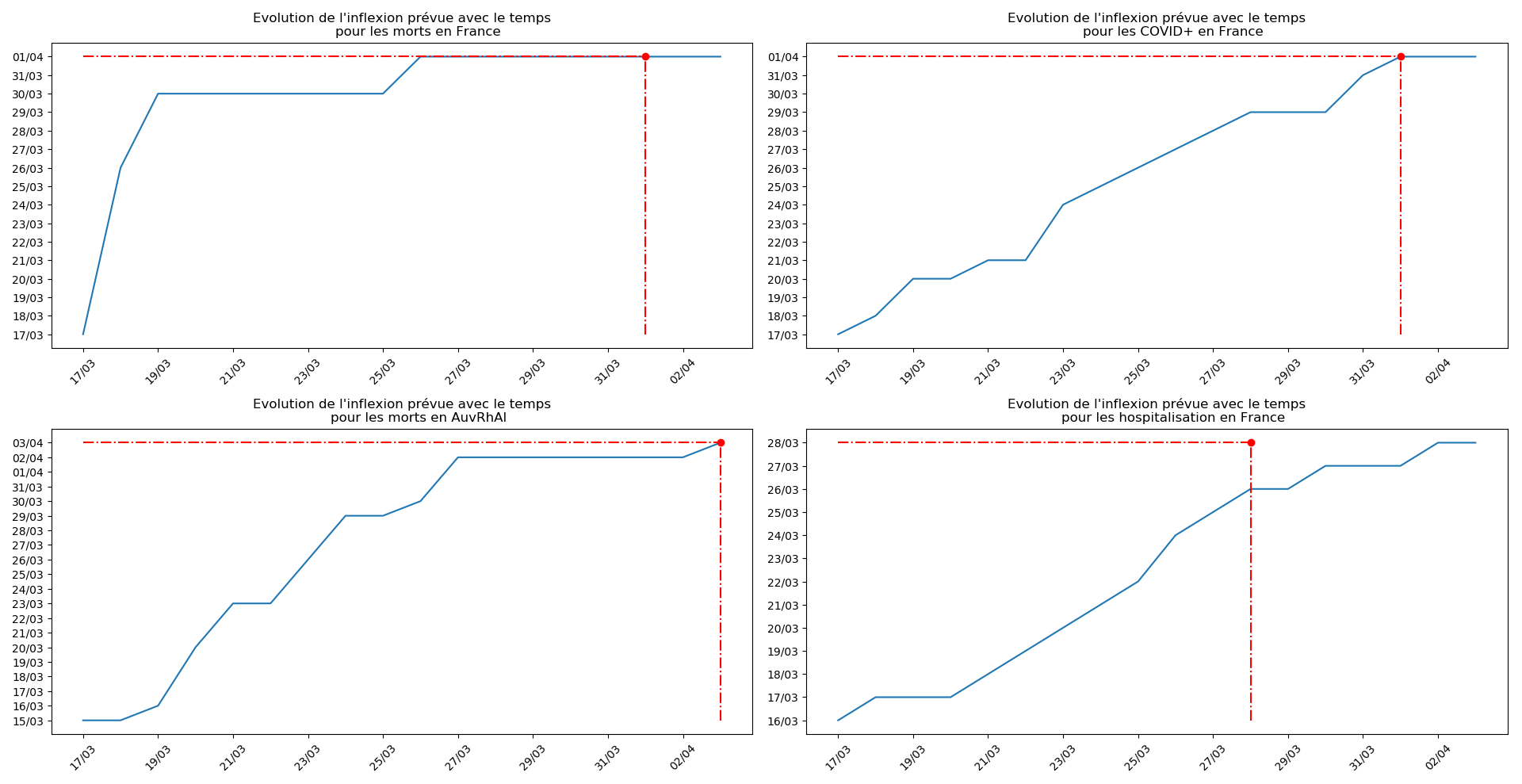
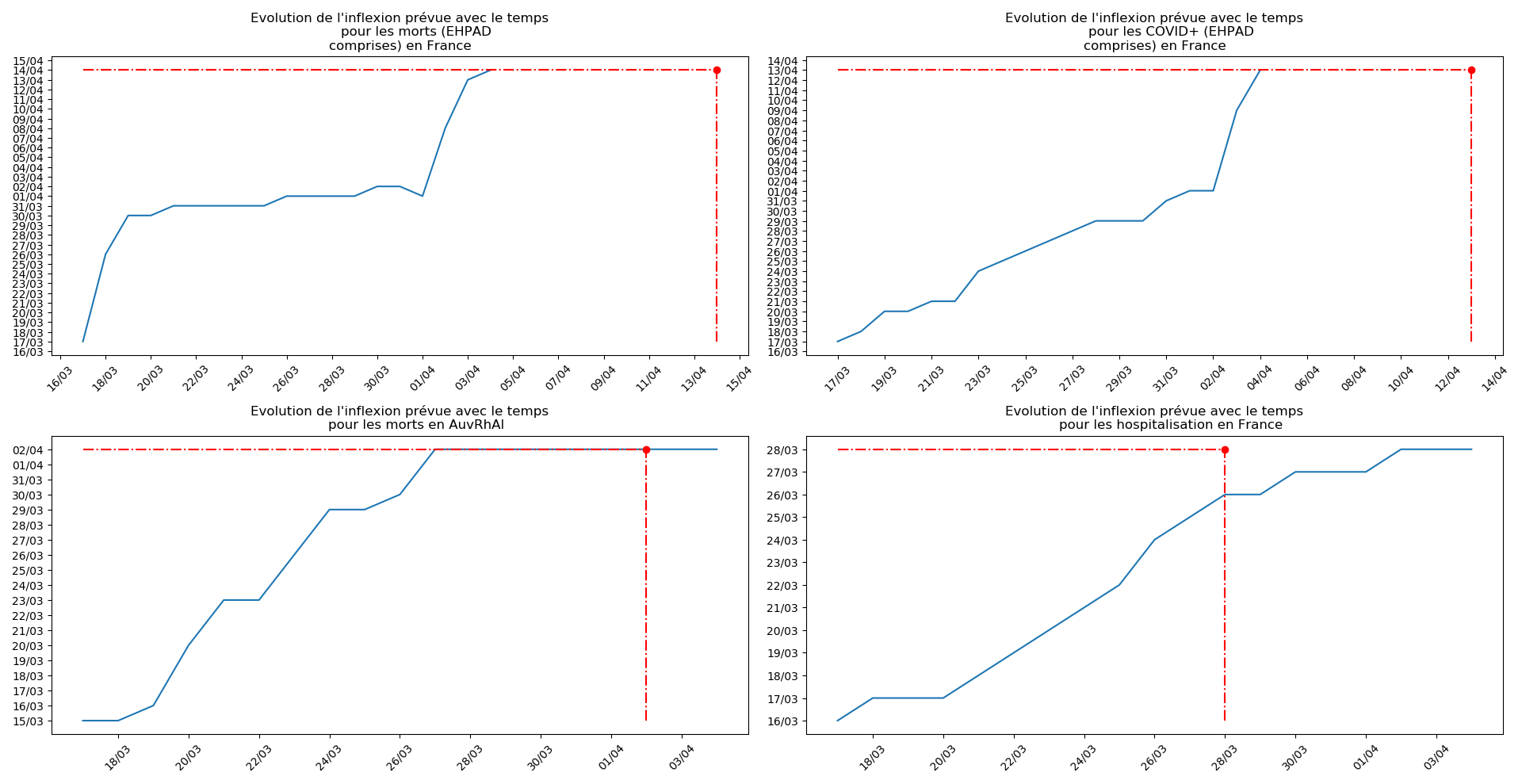
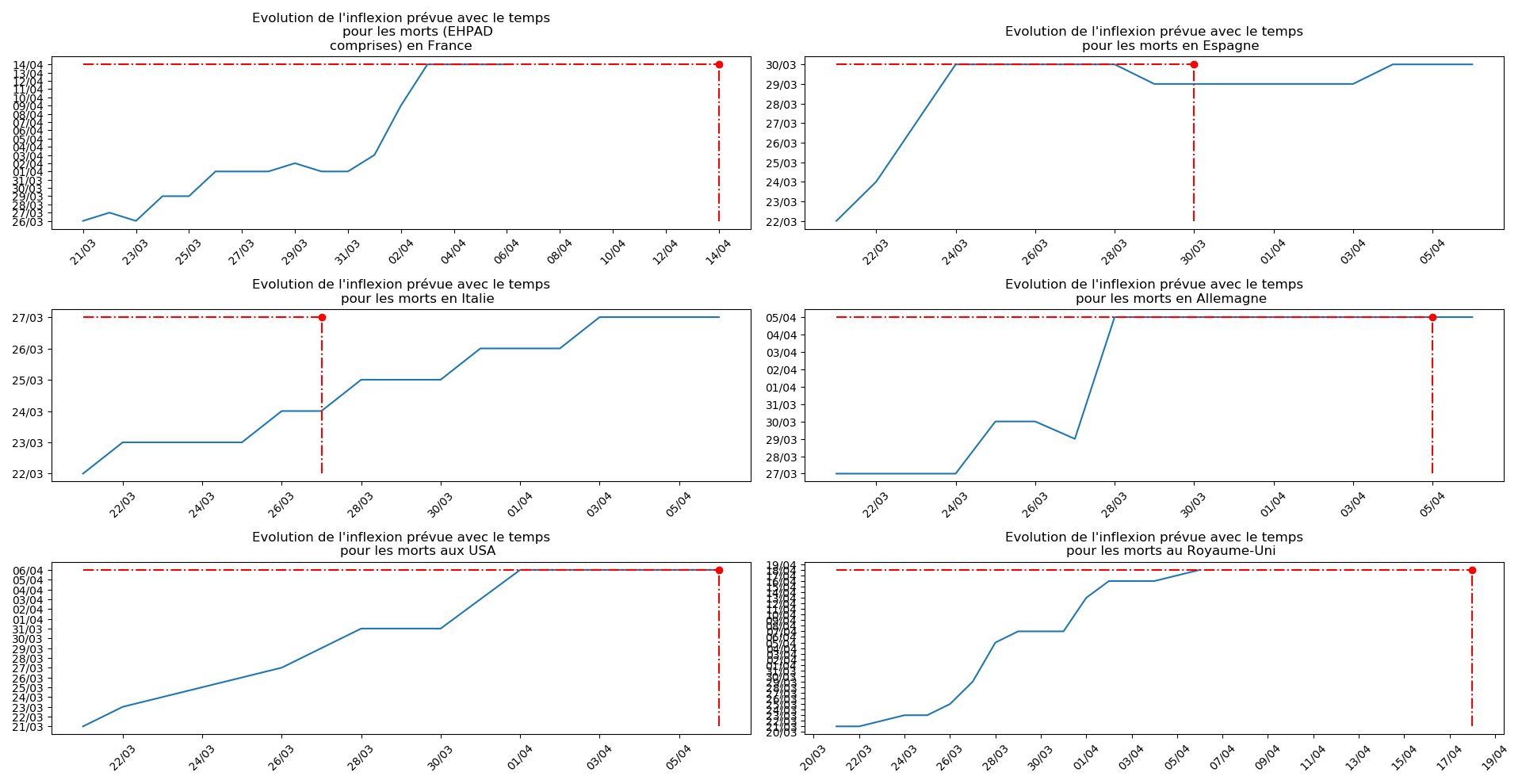
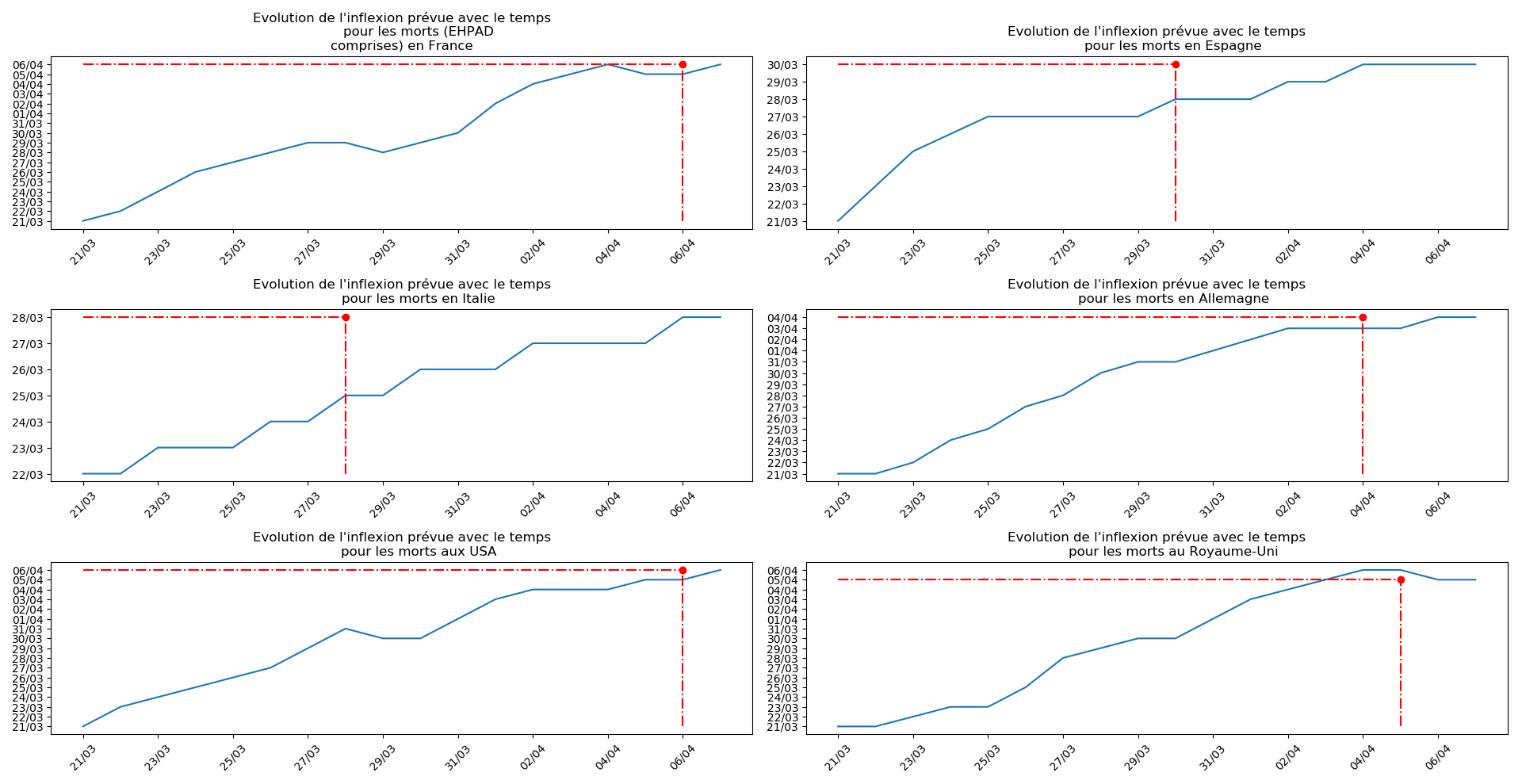
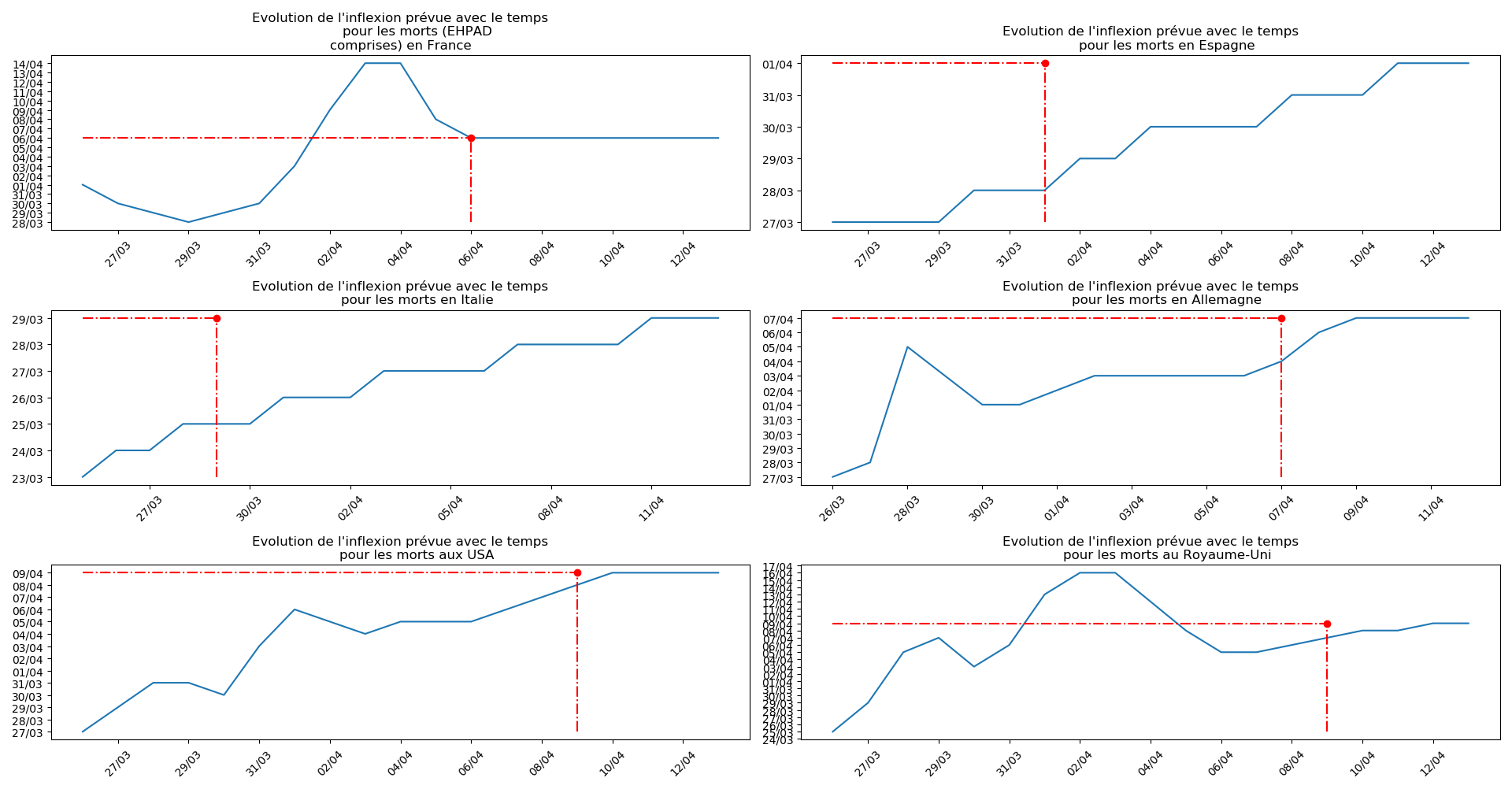
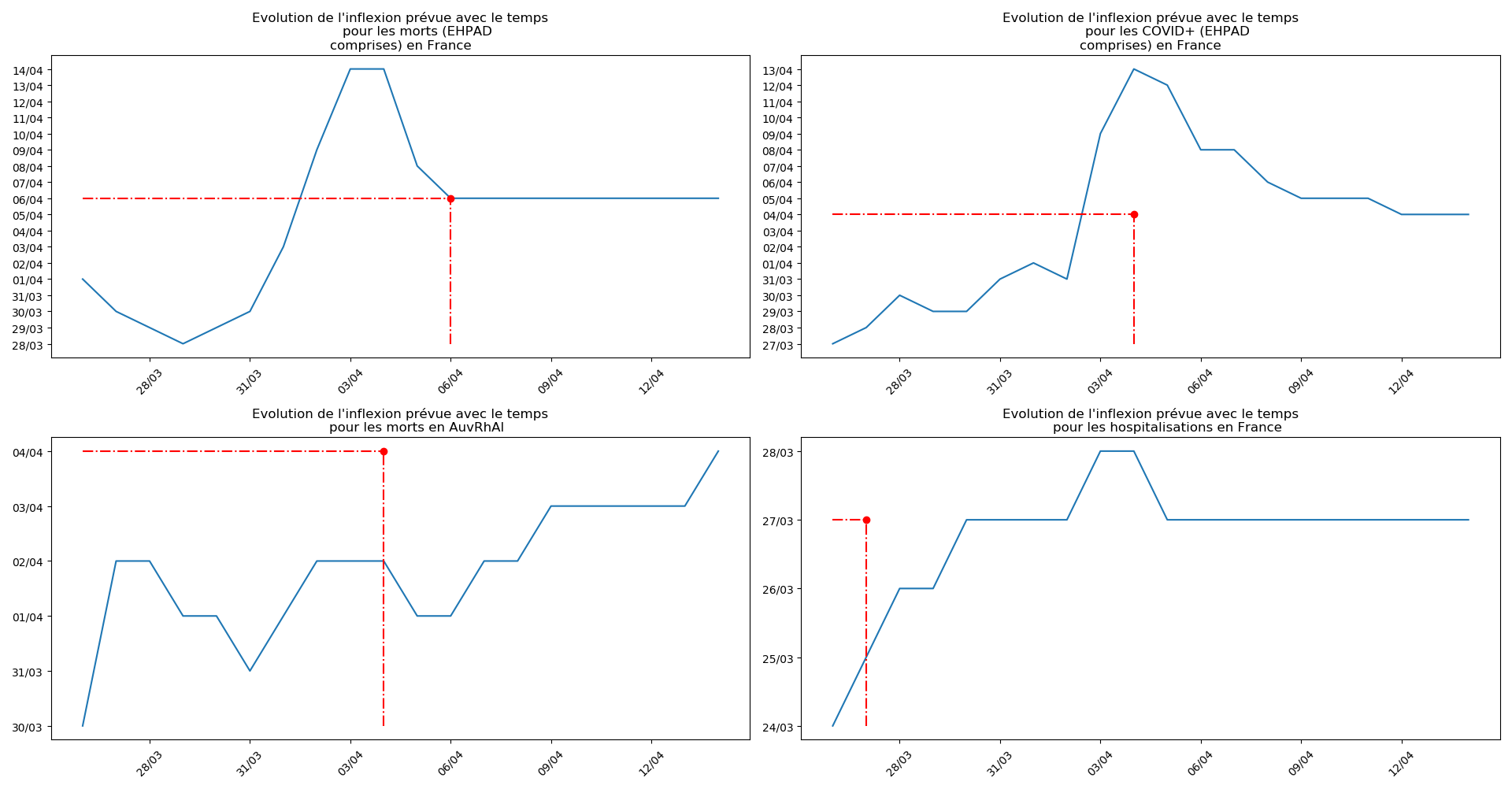
Lorsqu’on met bout-à-bout tous ces éléments (décomptes séparés des morts et CoViD+ en EHPAD/hors EHPAD, silence total jusqu’à il y a 3 jours sur les morts en EHPAD, décret sur la prescription du Rivotril en EHPAD jusqu’au 15 avril…), que l’on se rappelle par ailleurs que Salomon et les médecins du conseil scientifique insistaient sur le fait que les seules données ayant vraiment un sens étaient le nombre d’hospitalisation et que l’on regarde les prévisions actuelles de la méthode 2 concernant l’inflexion du nombre de CoViD+ en France, EHPAD comprises ou non…

… on peut se demander s’il n’y a pas une volonté délibérée de transformer les EHPAD en mouroirs pendant les 3 semaines où les hôpitaux français auraient été débordés par l’afflux des malades en provenant.

Si par ailleurs, la méthode 2 prévoit effectivement le bon ordre de grandeur pour le nombre de morts en France en fin d’épidémie - ce dont je doute, j’espère vraiment que l’algorithme est ici mis en défaut par la comptabilisation soudaine des morts en EHPAD -, ce serait le plus grand scandale sanitaire que la France ait jamais connu…

Libération apporte un démenti à mon hypothèse qui était - du coup - manifestement largement partagée. Pas sûr d’être convaincu, mais les arguments présentés sont crédibles.

Le Média au contraire alimente la thèse d’une mortalité largement sous-estimée par le gouvernement… À suivre.

Monde

À côté de ce qu’il se passe en France depuis quelques jours, le reste du monde paraît totalement épargné par la maladie, même les USA. Seul le Royaume-Uni semble dans une situation aussi critique que la France :

Pourquoi ? Je ne sais pas. La capacité de la méthode 2 à prévoir, dans les autres situations, les bons paramètres pour la sigmoïde me sidère un peu. La seule différence avec les deux autres méthodes, c’est que je prends en compte des termes non linéaires.

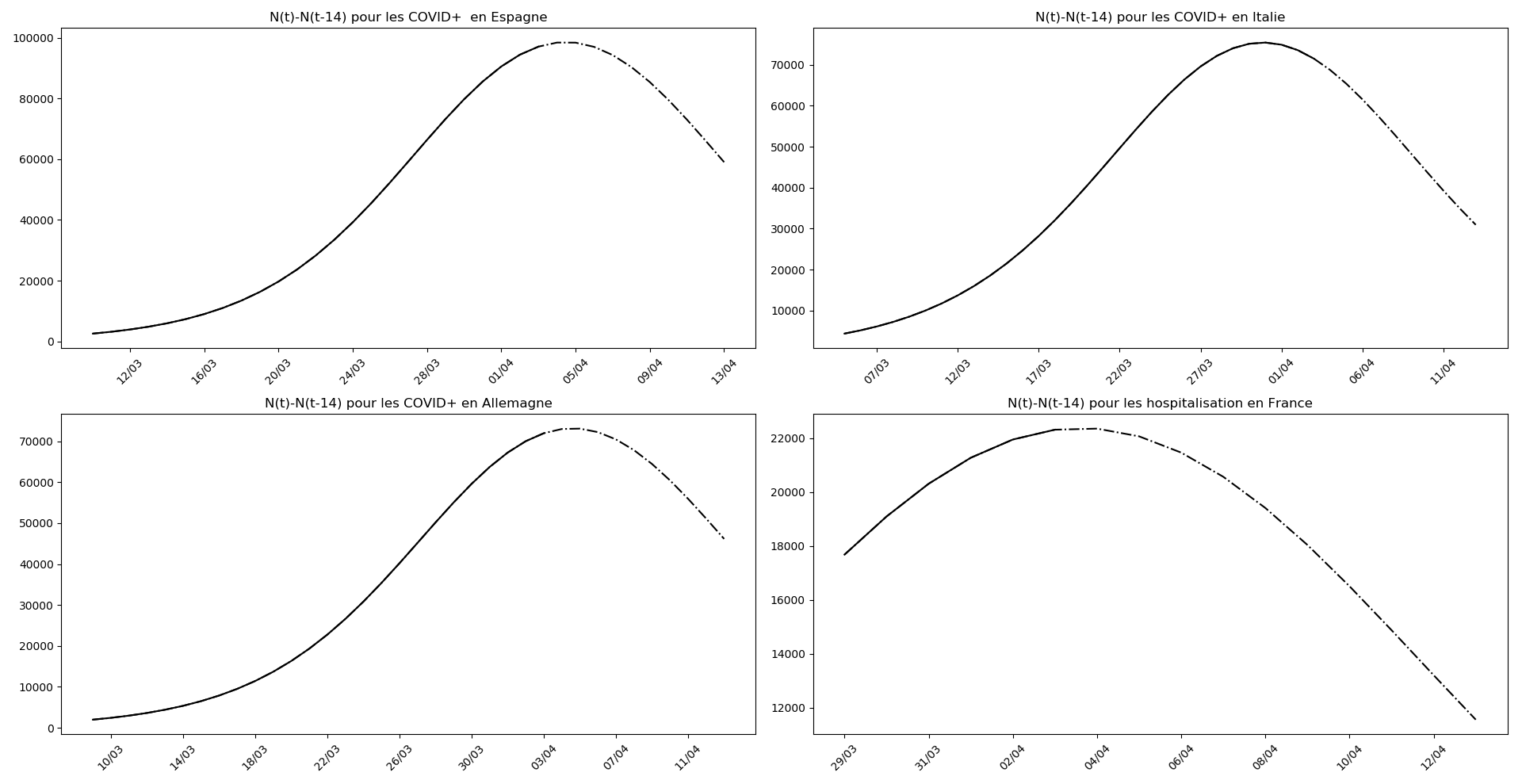
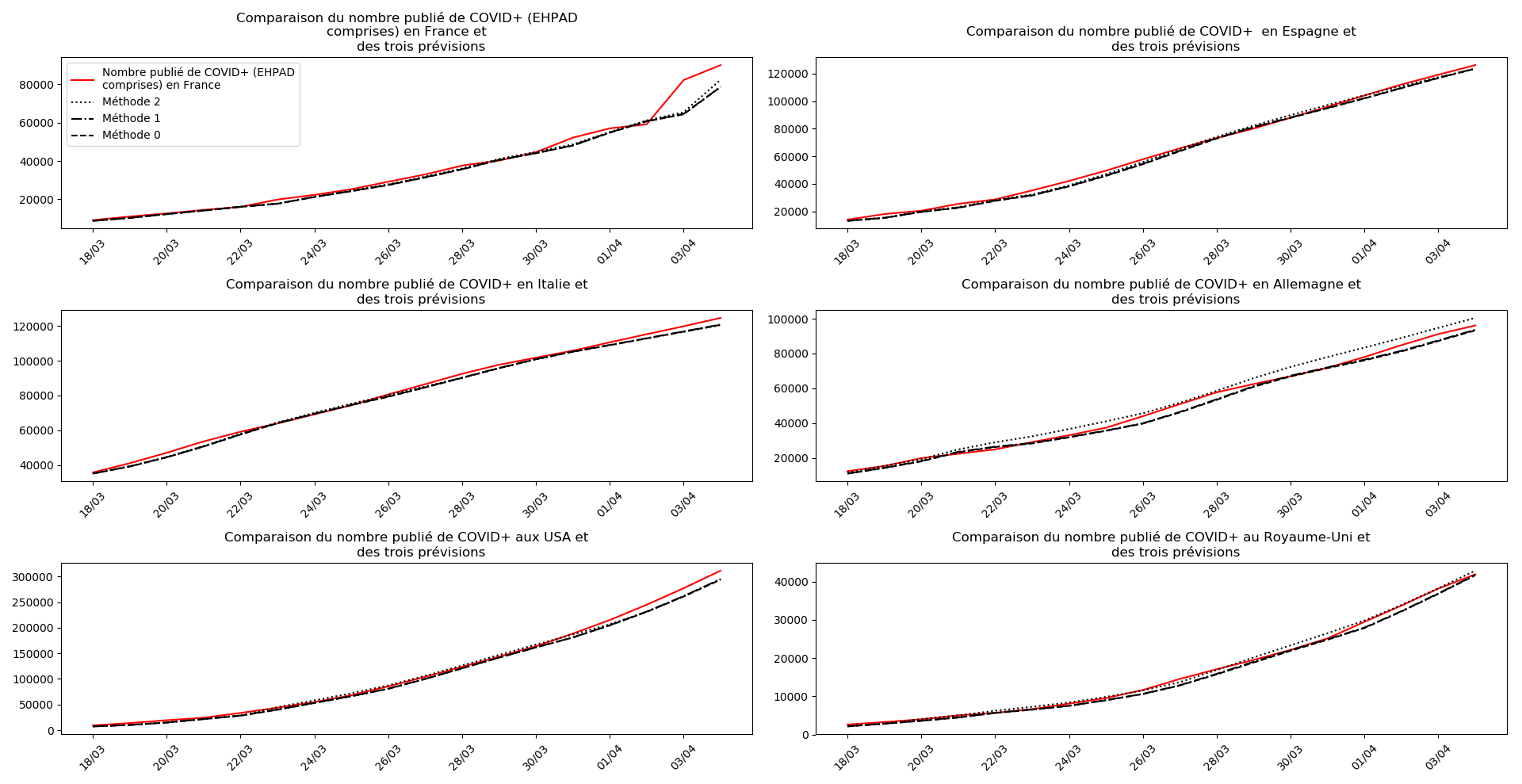
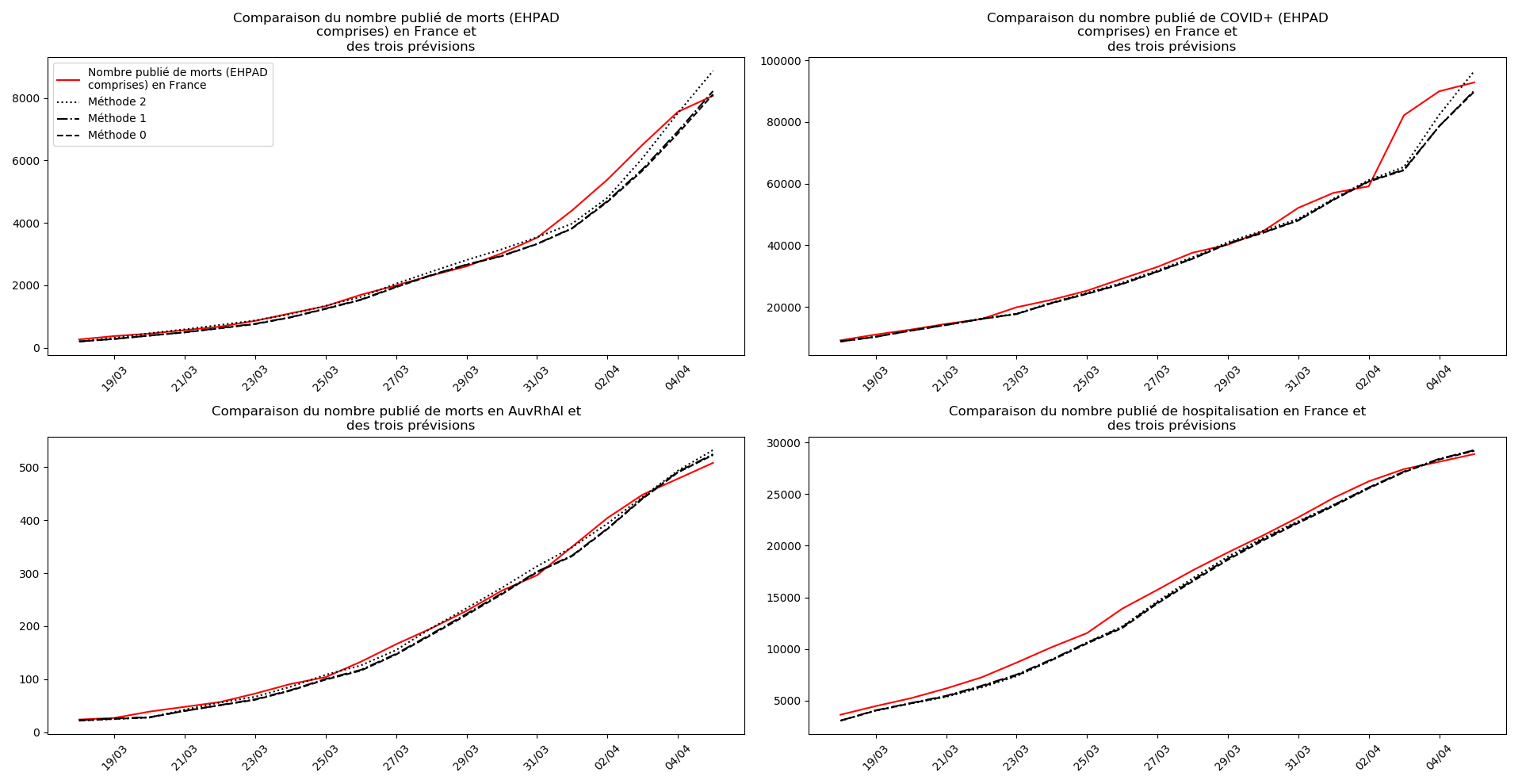
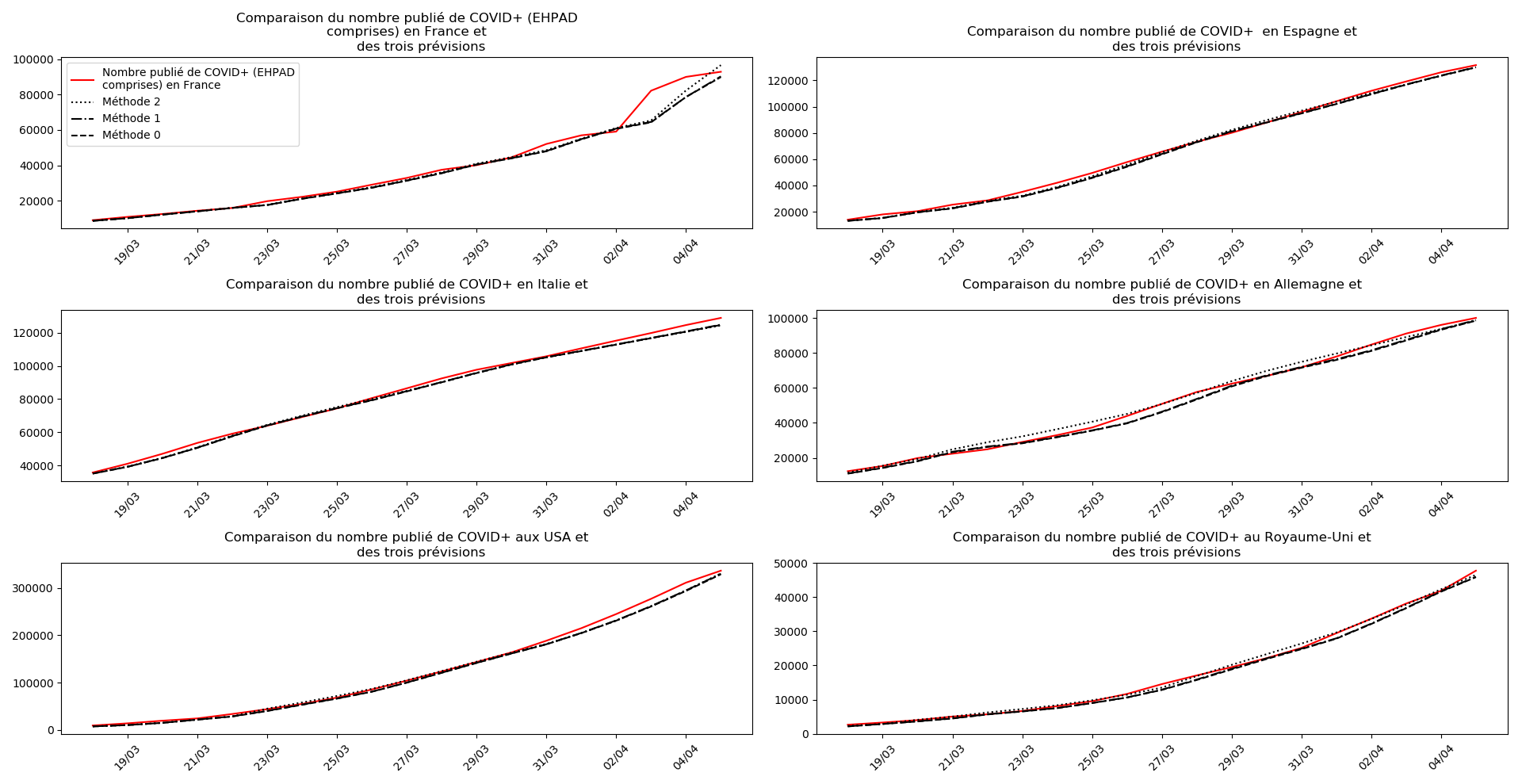
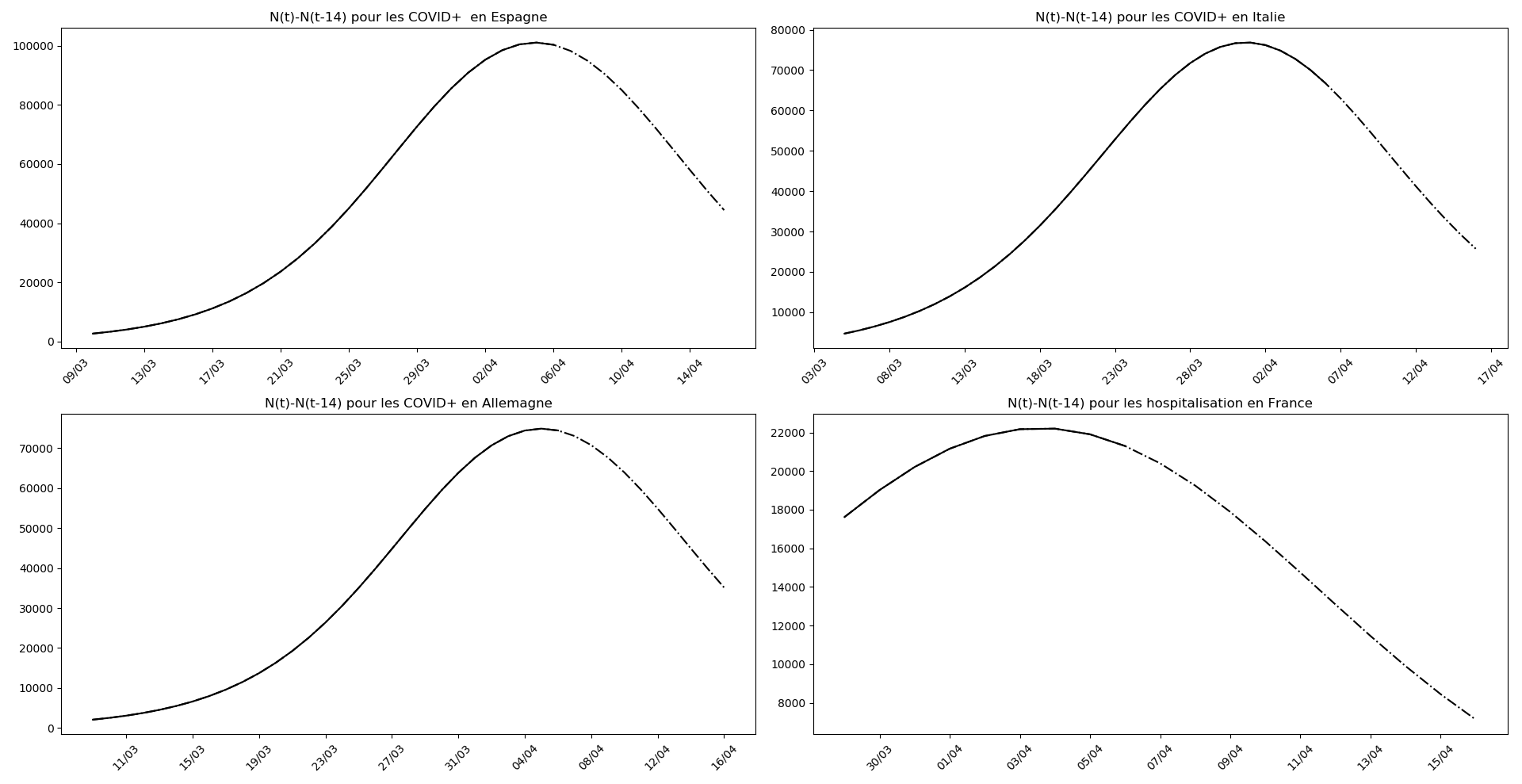
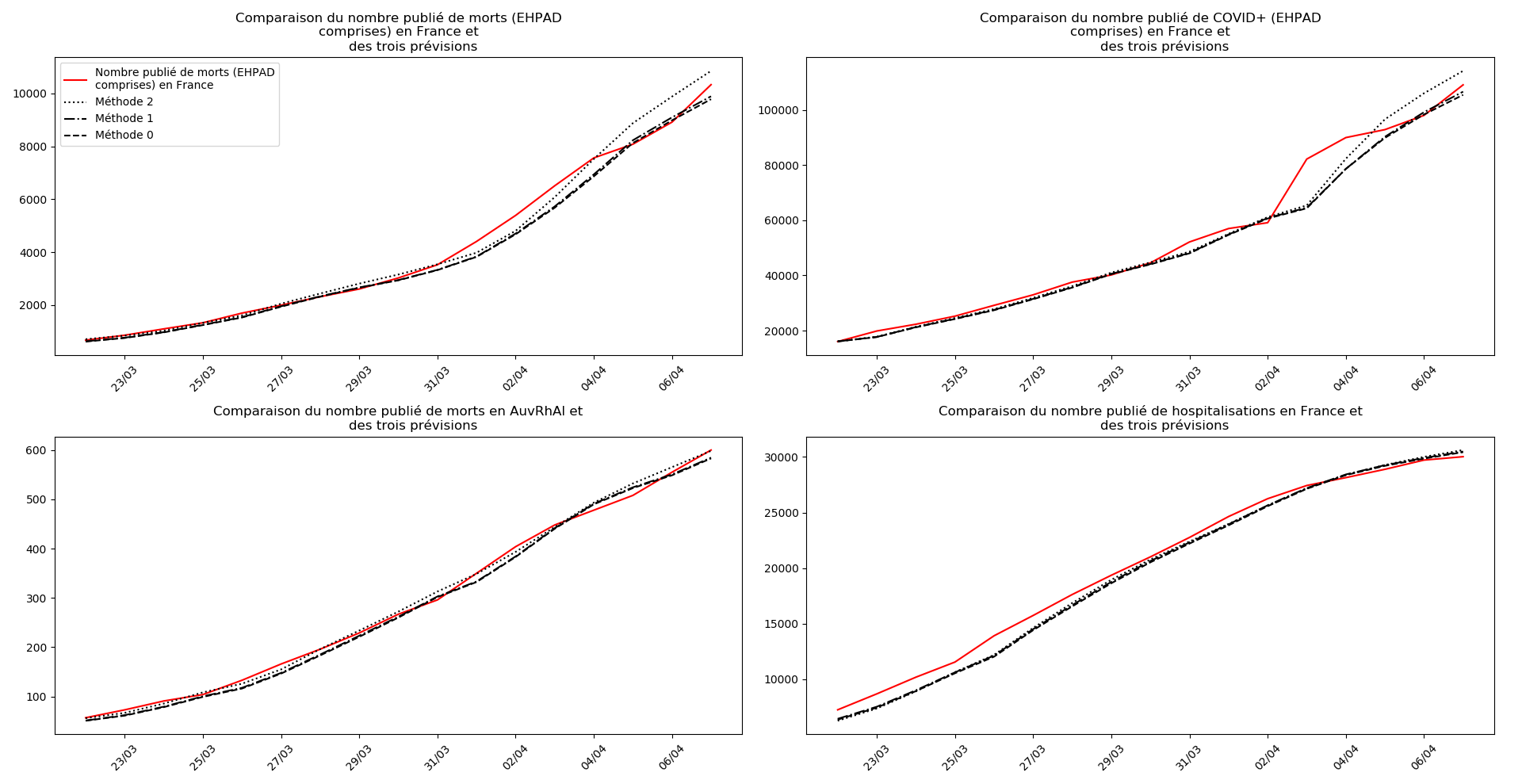
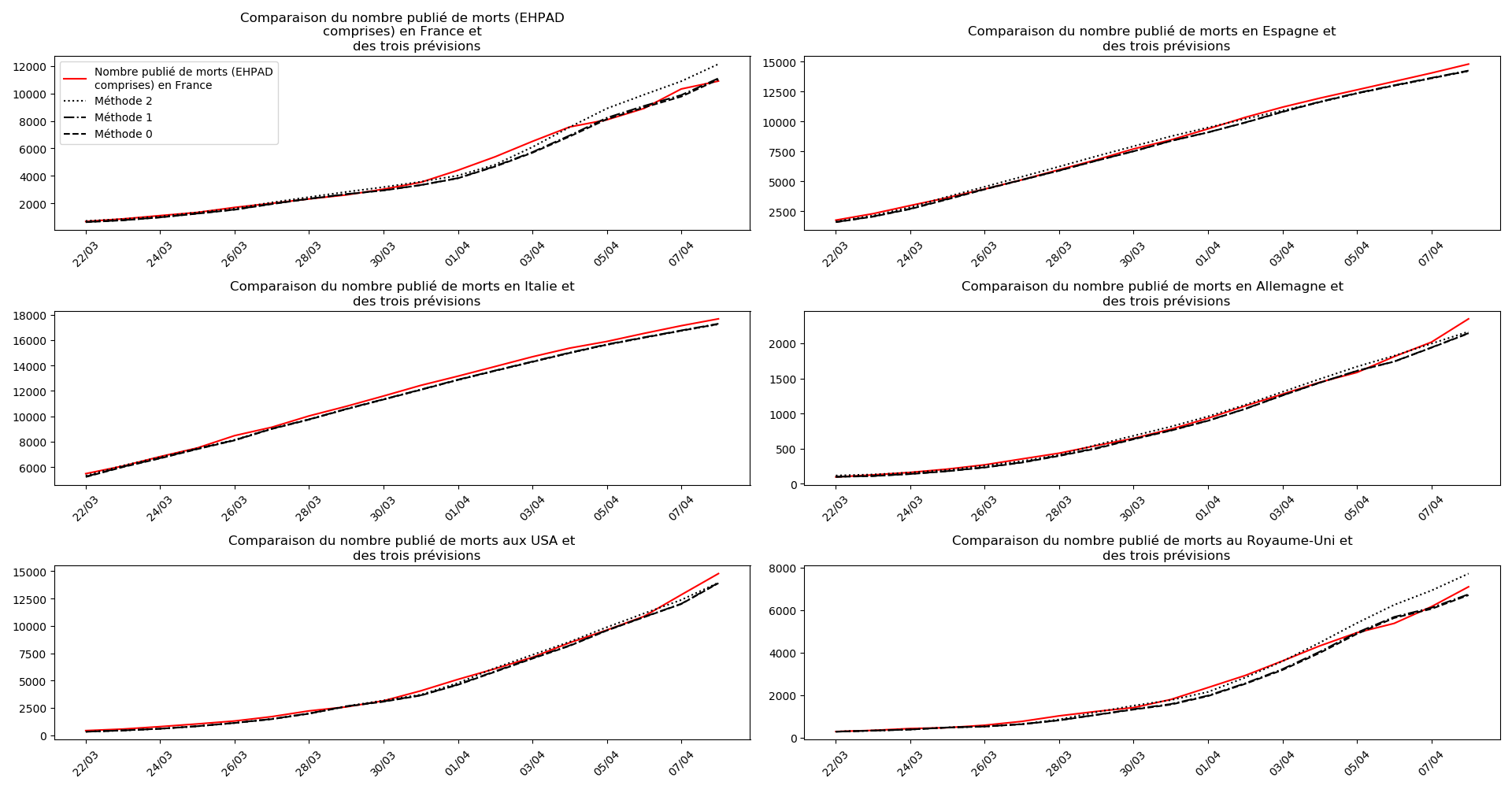
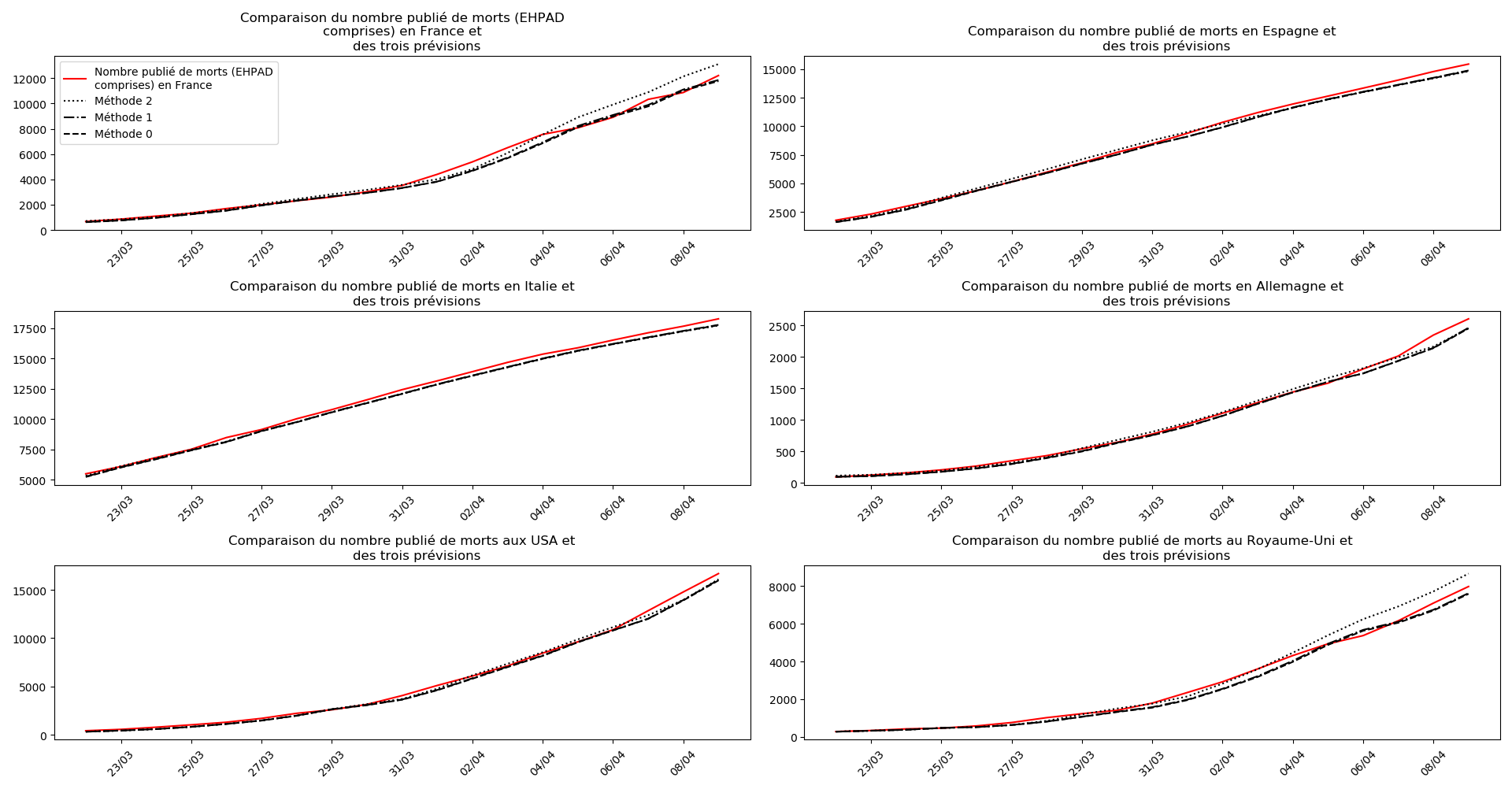
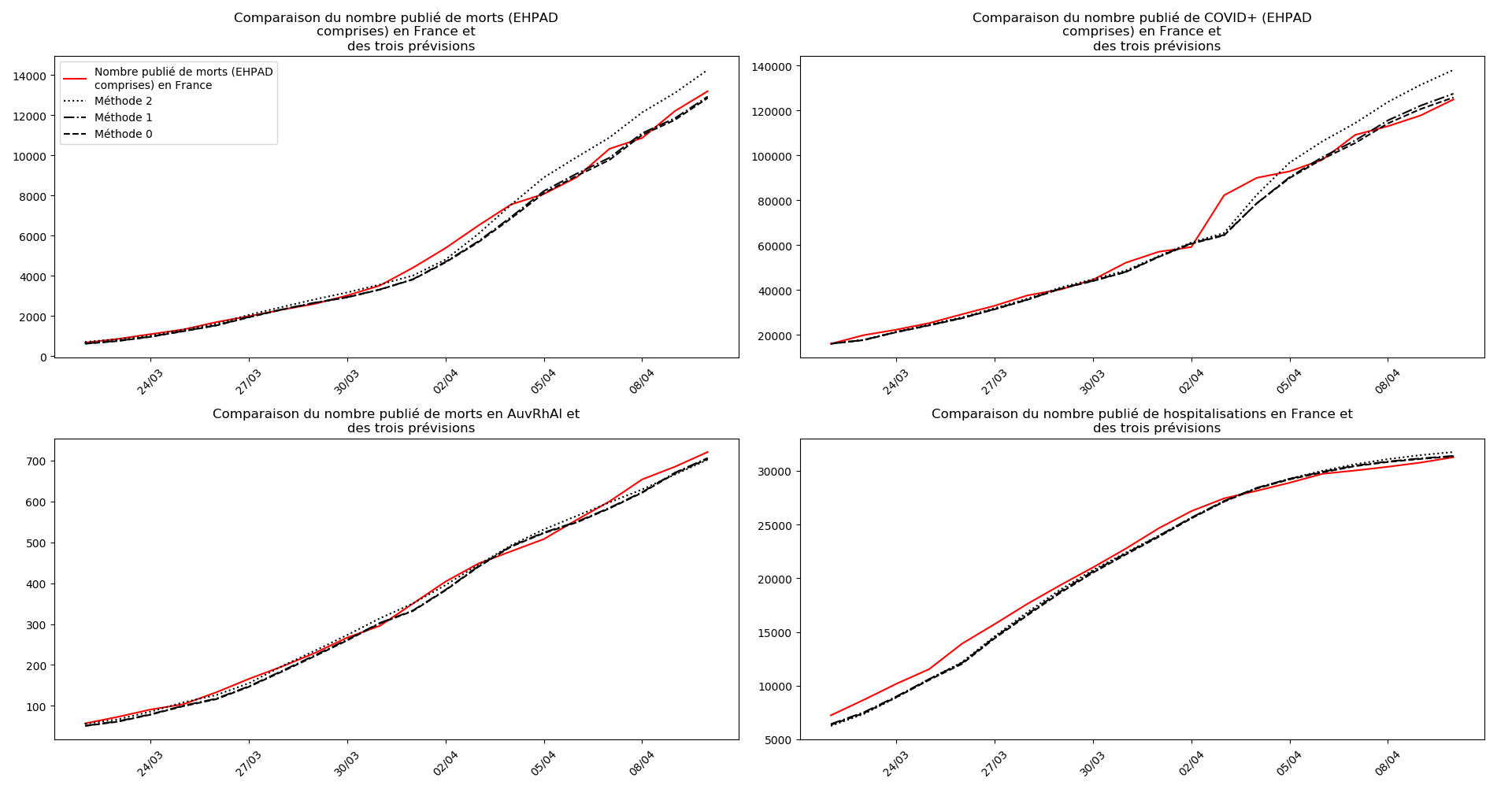
On ne peut que constater qu’elle prédit correctement le nombre de nouveaux cas du jour au lendemain, donnant une fourchette haute, tandis que les deux autres méthodes donnent une fourchette basse :

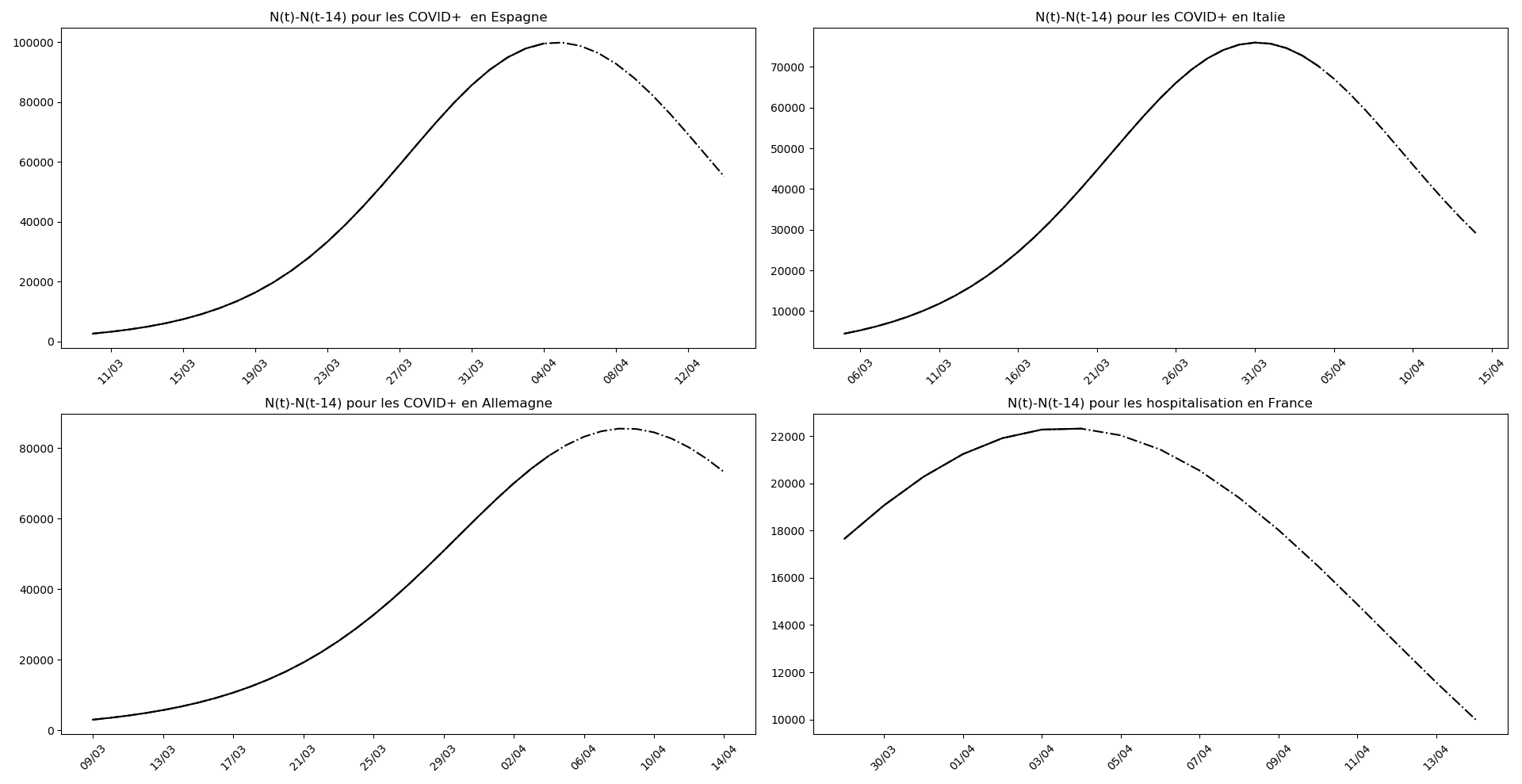
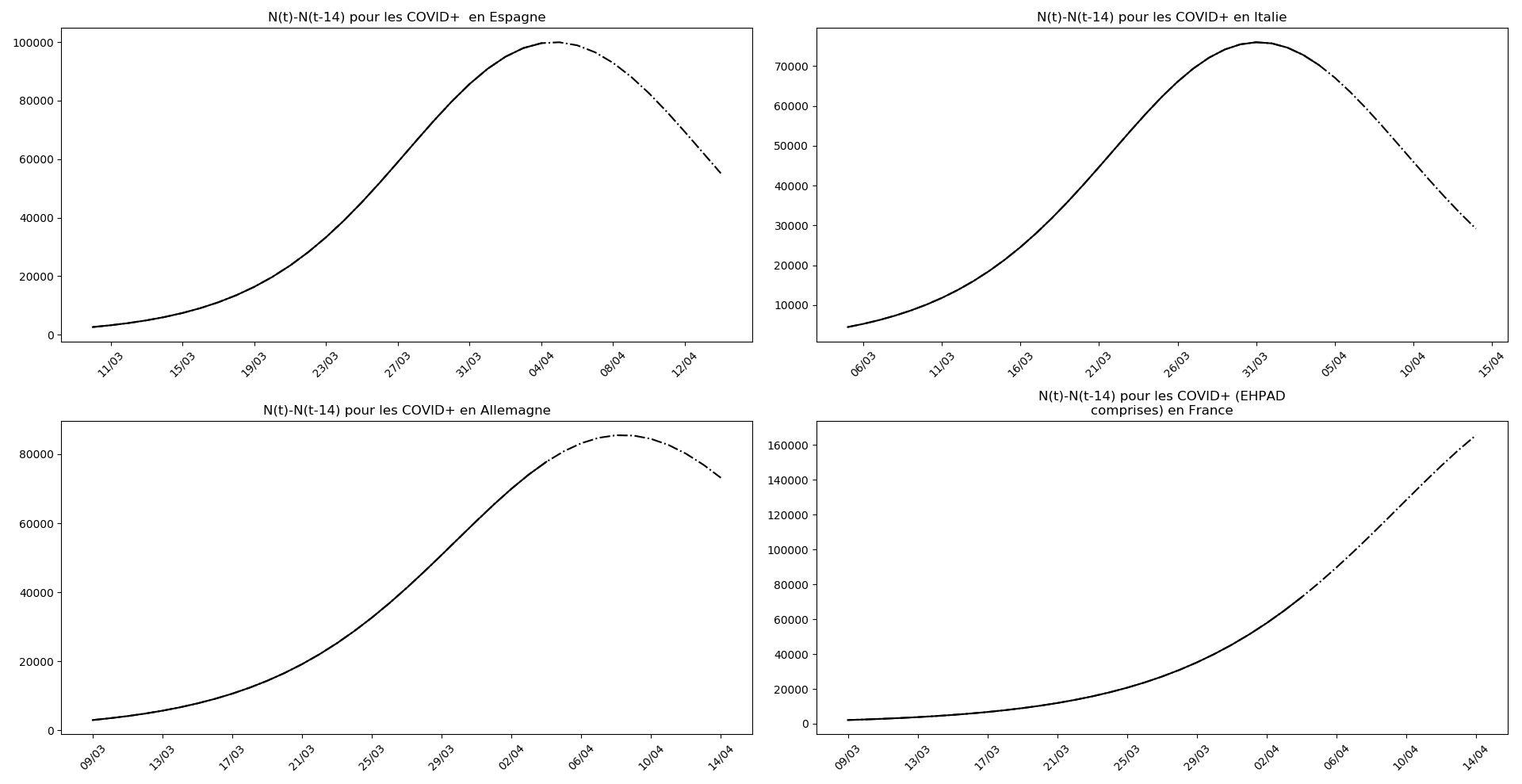
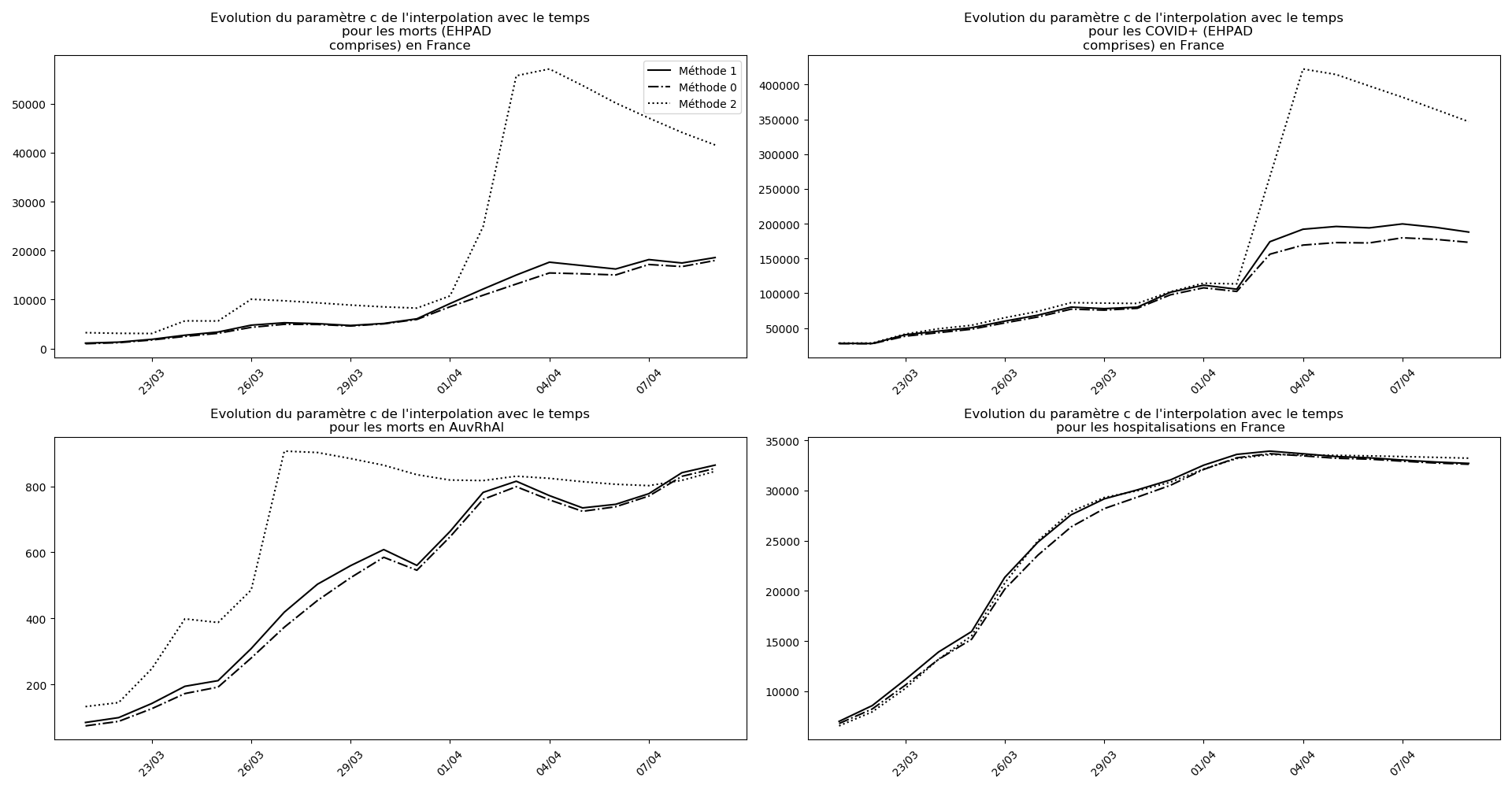
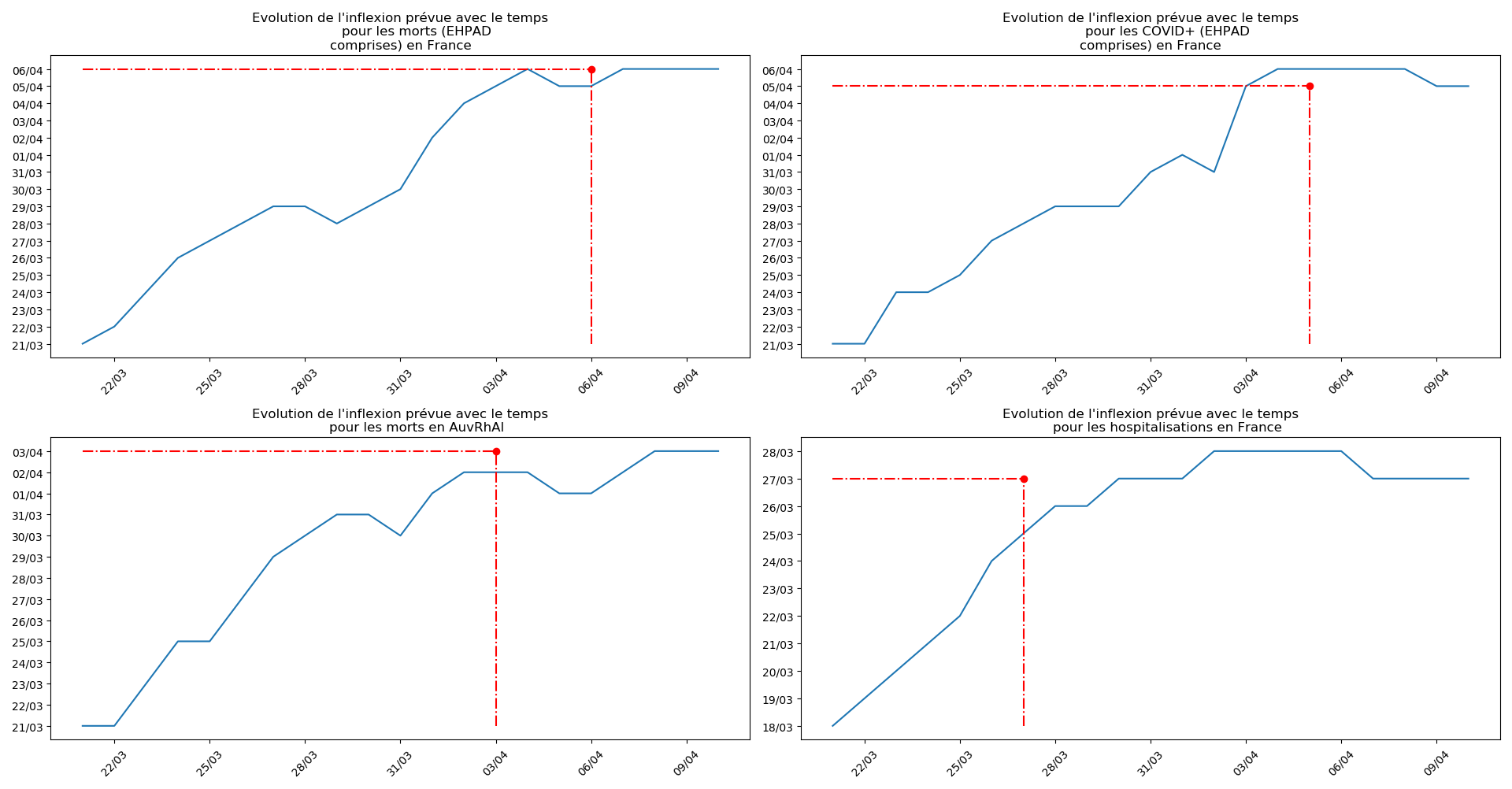
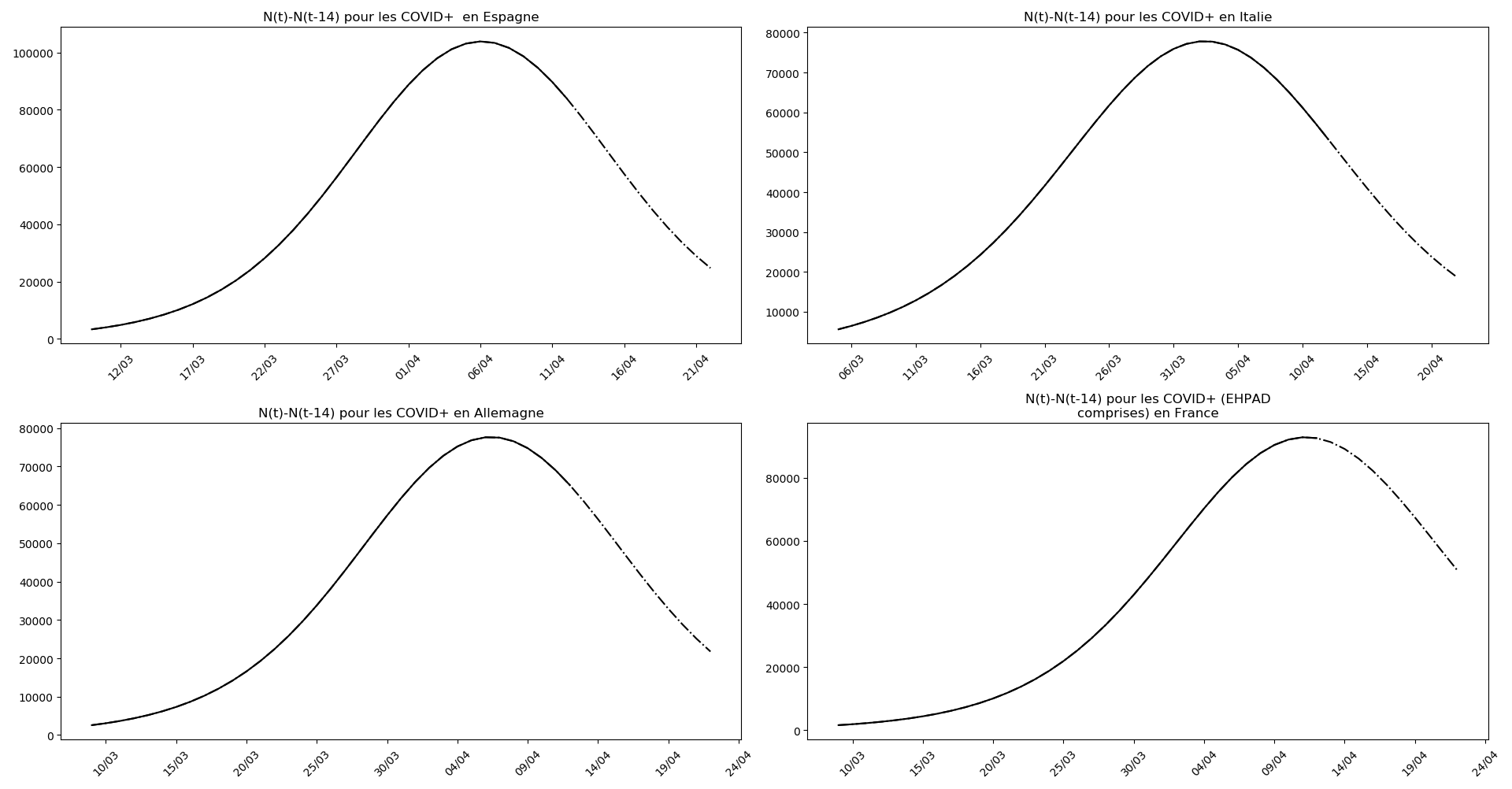
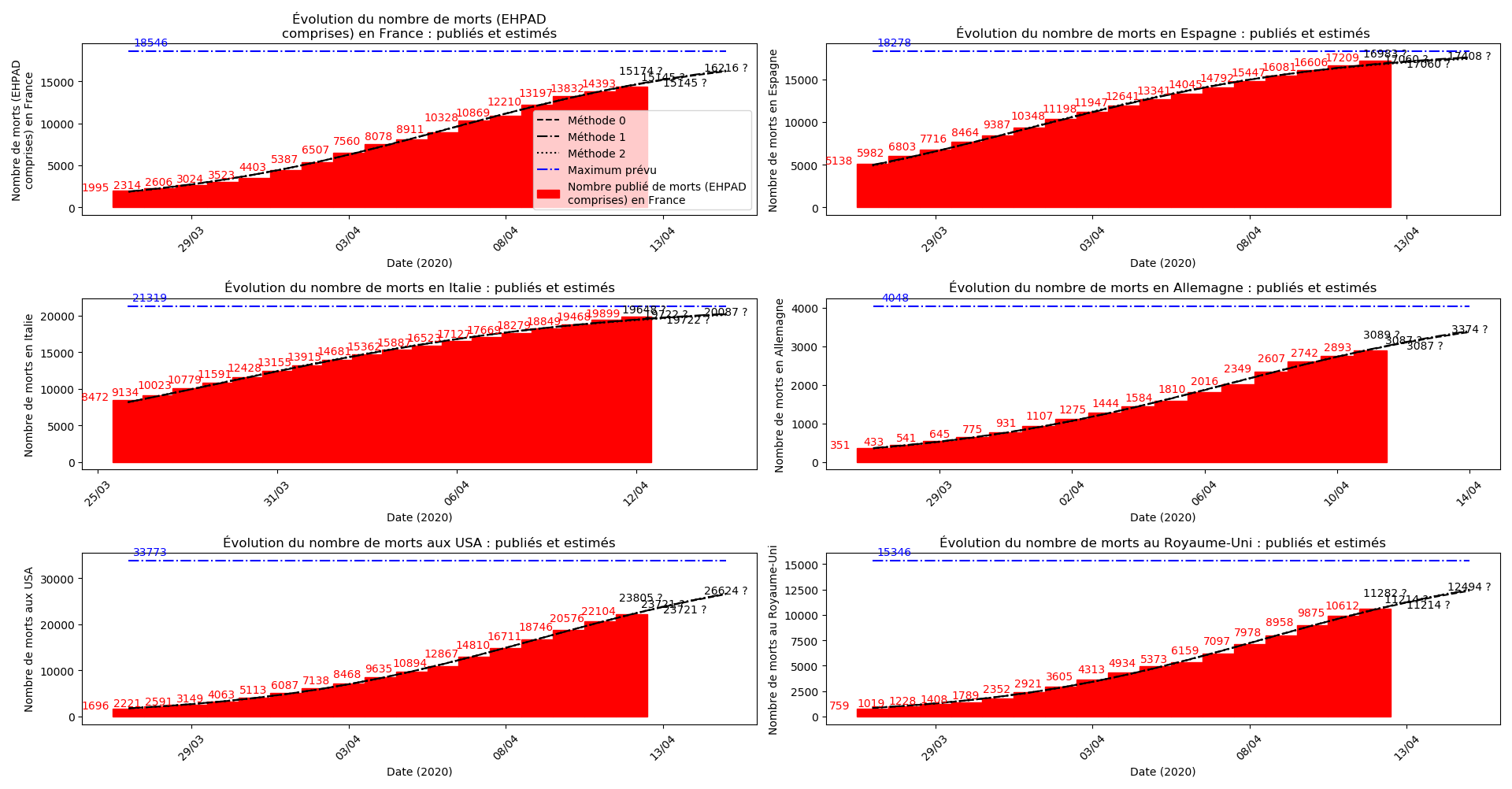
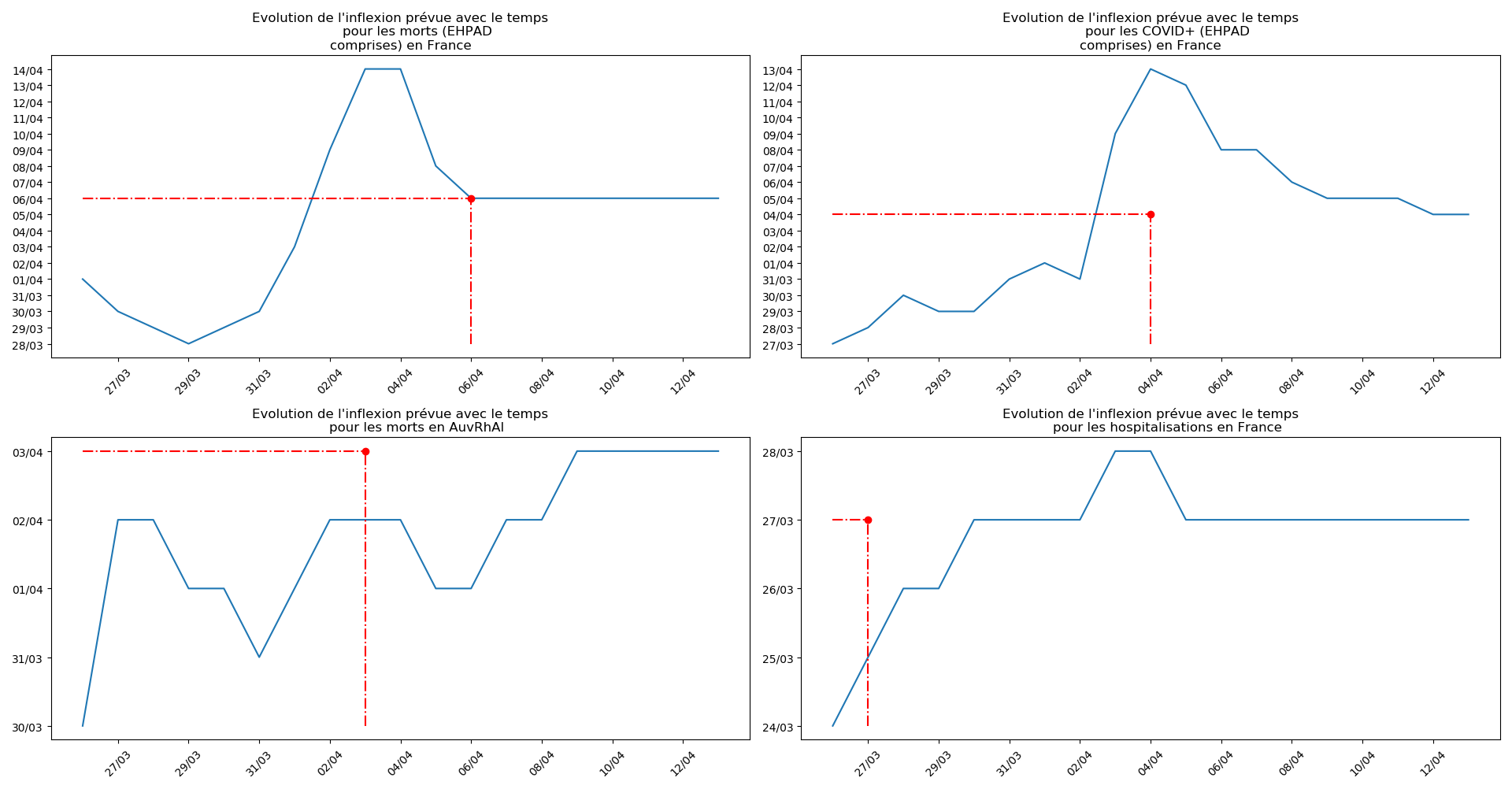
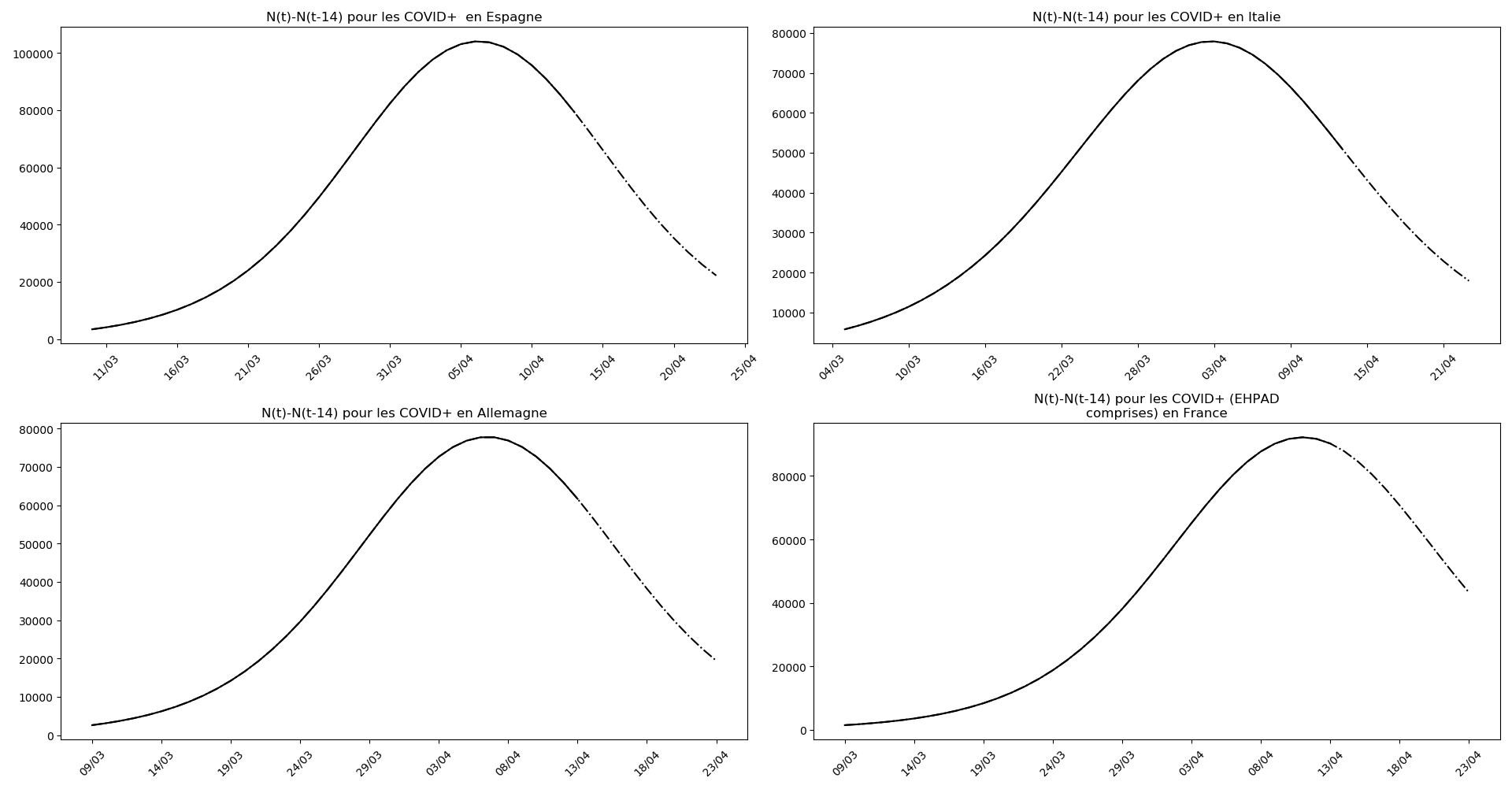
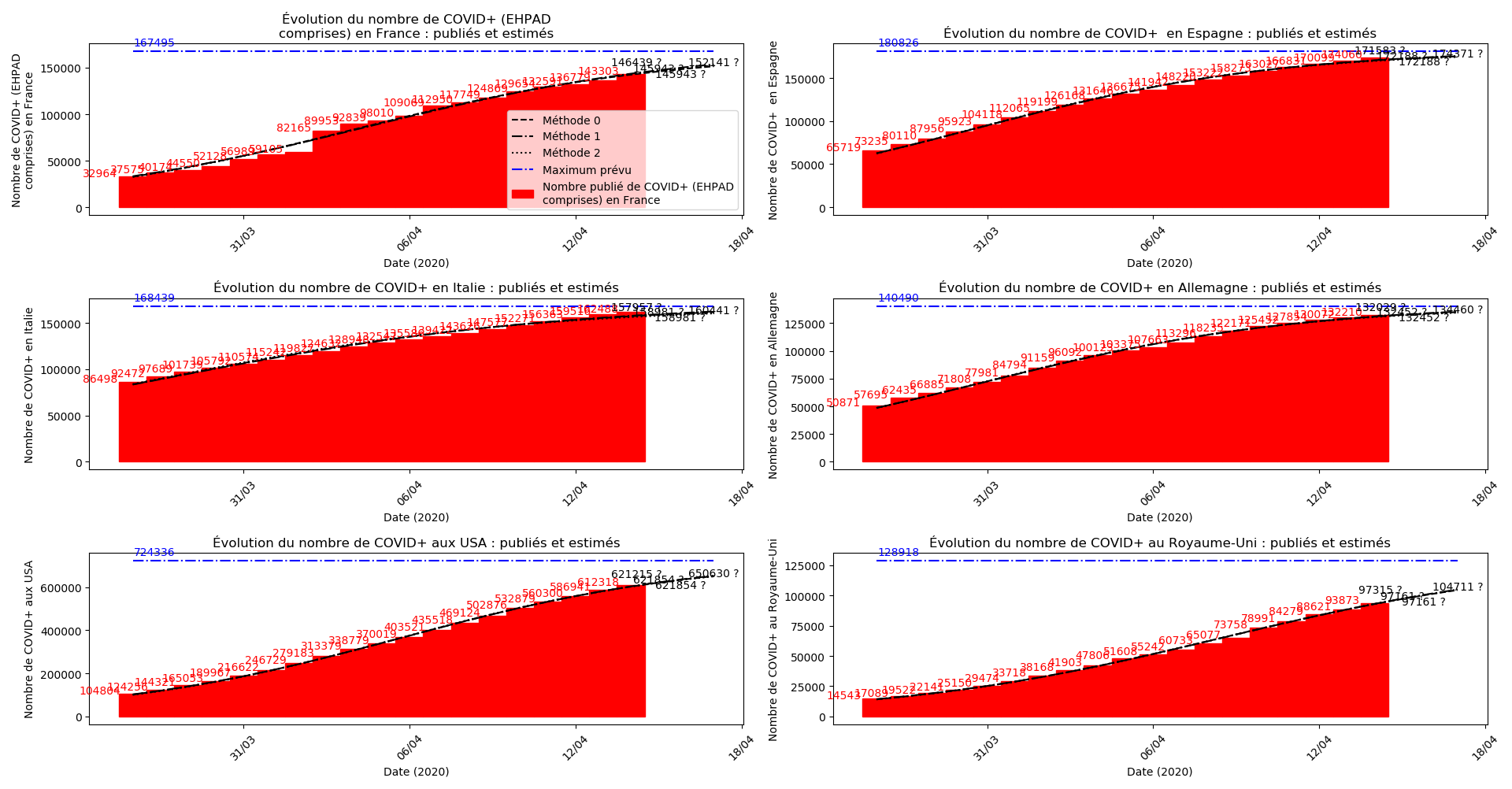
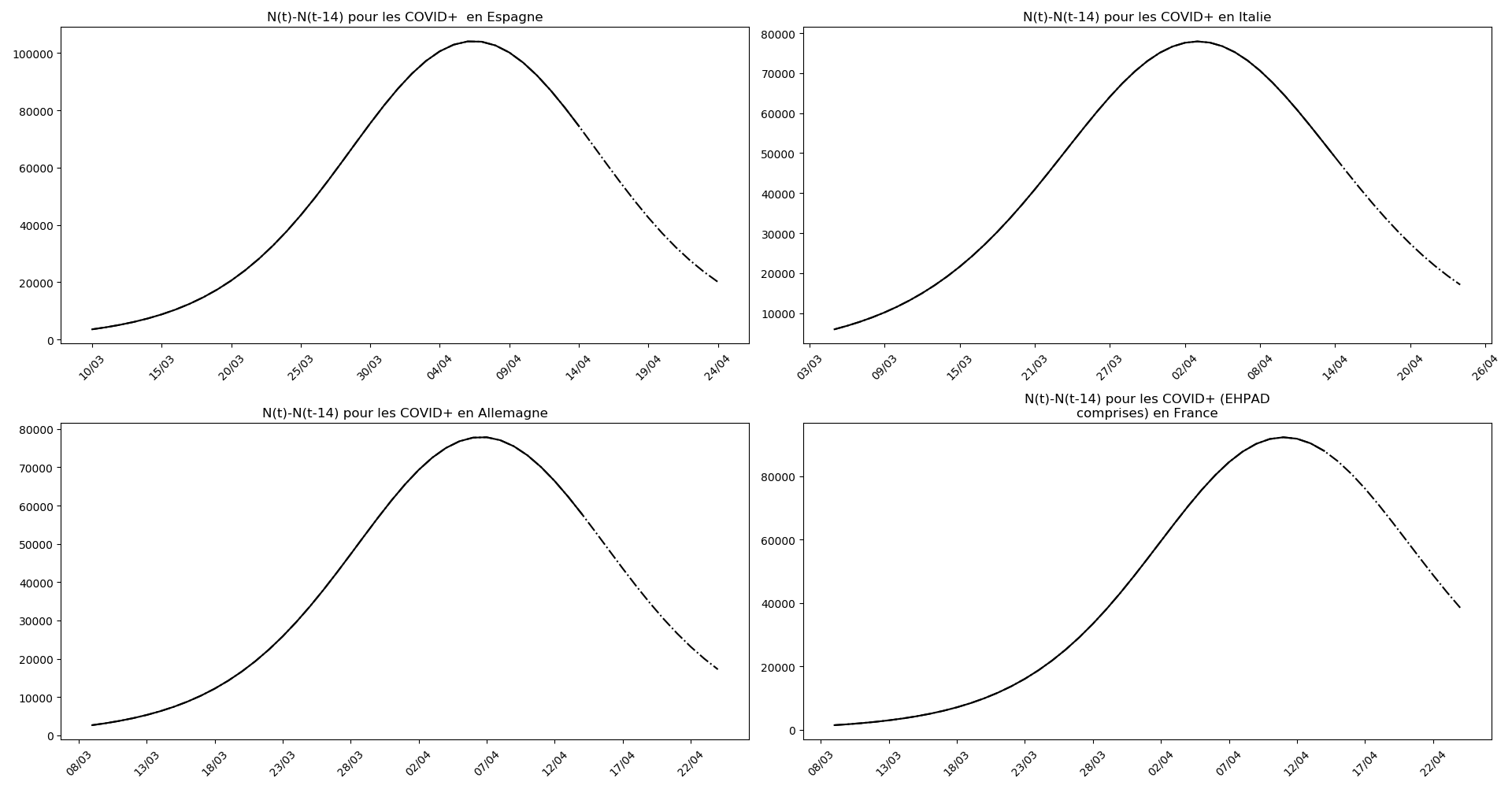
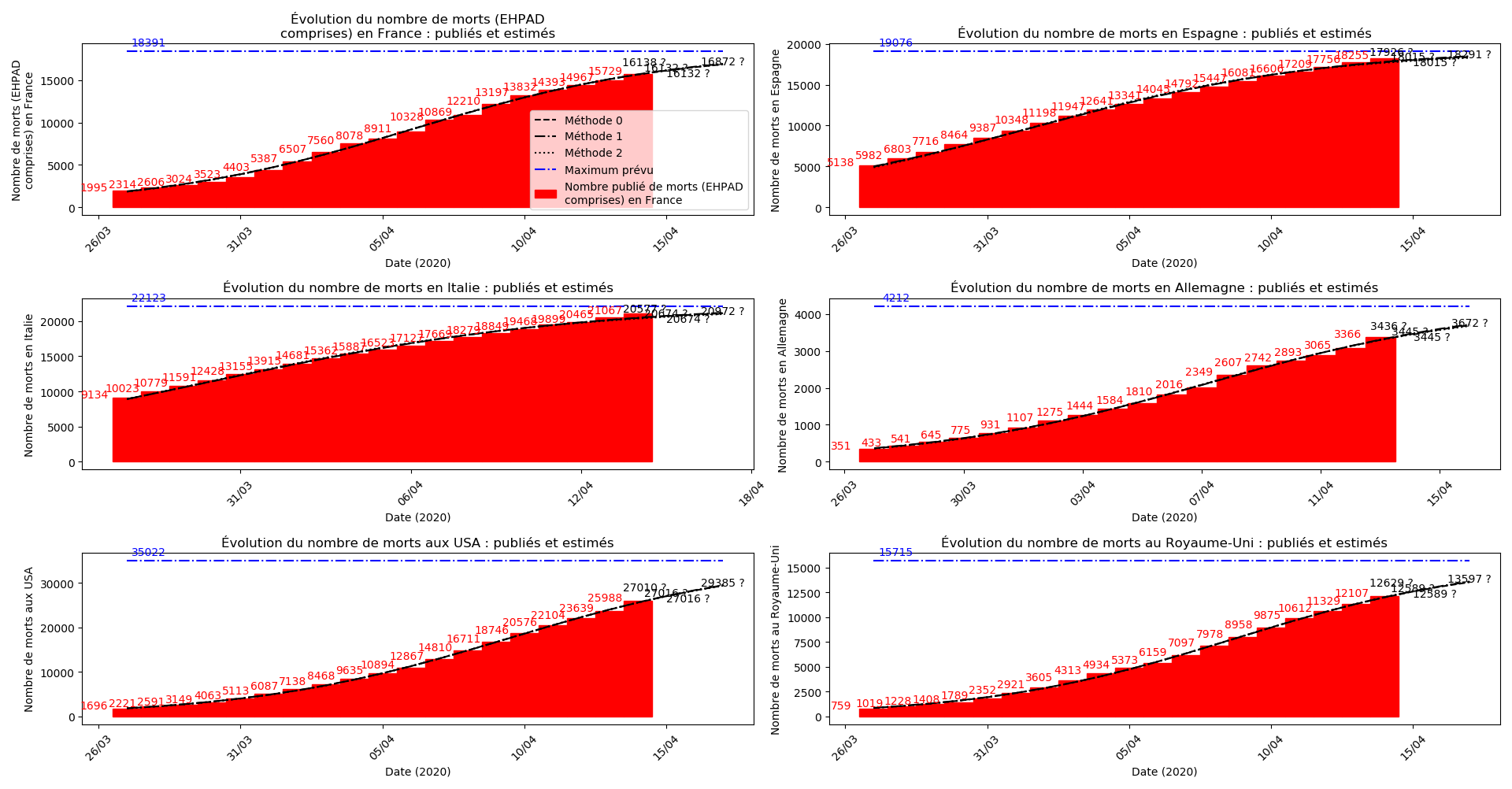
Enfin, voici les prévisions pour demain et les pics prévus, avec pour la France, une différence drastique suivant que l’on regarde le pic des hospitalisations (espoir !) ou celui des CoViD+, EHPAD comprises…

Situation au 5 avril

Sources

J’ai légèrement modifié la méthode 2 pour qu’elle prenne plus rapidement en compte l’amélioration (à la baisse) de la situation.

Par ailleurs, les données du jour en France laissent penser que la situation est bien meilleure que ce que la prise en compte des cas et des décès en EHPAD laissait augurer. Il faut être circonspect, j’ai remarqué que les données du week-end étaient toujours plus faibles que prévu lors des semaines précédentes.

Nouveauté : calcul des coefficients de corrélation :

['morts (EHPAD\ncomprises) en France', 0.9989688791822391]
['COVID+ (EHPAD\ncomprises) en France', 0.9981935665182897]
['morts en Espagne', 0.9998631623550266]
['COVID+  en Espagne', 0.9999123590710906]
['morts en Italie', 0.9999131007973785]
['COVID+ en Italie', 0.999879751936839]
['morts en Allemagne', 0.999261676179739]
['COVID+ en Allemagne', 0.9997437337631007]
['morts aux USA', 0.9999047226521878]
['COVID+ aux USA', 0.9998417808770862]
['morts au Royaume-Uni', 0.9993110053204941]
['COVID+ au Royaume-Uni', 0.9999061319592014]
['morts en AuvRhAl', 0.9997297335682387]
['COVID+ en AuvRhAl', 0.9997402816063816]
['hospitalisation en France', 0.9999393496674048]

France

Monde

Situation au 6 avril

Sources

J’ai décalé le premier jour de la simulation. J’ai fait quelques autres menus changements, notamment j’utilise la valeur asymptotique fournie par la méthode 1 plutôt que par la méthode 2 pour éviter l’effet de sur-évaluation dû à la prise en compte tardive des morts en EHPAD en France.
Je maintiens qu’il faudra faire toute la lumière sur l’accès aux soins en hôpitaux en France pendant la crise, sur la communication par le gouvernement du nombre de victimes du CoViD-19 et sur sa responsabilité dans le nombre de décès en EHPAD notamment : Le Média.

Voici par exemple la comparaison entre les nombres de morts au mois de mars en France pour les années 2018, 2019 et 2020 que l’INSEE publie :

Ce qui laisse à penser que le nombre de morts dûs au CoViD-19 au 27 mars est deux fois supérieur à celui avancé par le gouvernement…

Coefficients de corrélation (ceux d’hier étaient calculés avec pondération, ceux d’aujourd’hui sans) :

['morts (EHPAD\ncomprises) en France', 0.9983121282990342]
['COVID+ (EHPAD\ncomprises) en France', 0.9978647545478574]
['morts en Espagne', 0.9998106693554795]
['COVID+  en Espagne', 0.9998927658035403]
['morts en Italie', 0.999831155092719]
['COVID+ en Italie', 0.9997930991846969]
['morts en Allemagne', 0.9997711702572081]
['COVID+ en Allemagne', 0.999721966964169]
['morts aux USA', 0.9998272886536839]
['COVID+ aux USA', 0.9997084120584774]
['morts au Royaume-Uni', 0.997751087031677]
['COVID+ au Royaume-Uni', 0.9998650405180955]
['morts en AuvRhAl', 0.9997363099502332]
['COVID+ en AuvRhAl', 0.99958465387001]
['hospitalisation en France', 0.9997583473334203]

Les coefficients de corrélation font notamment apparaître la piètre performance de l’interpolation du nombre de morts au Royaume-Uni et en France.

France

Monde

À moins d’un revirement malheureux, l’Espagne et l’Italie semblent tirées d’affaire :

Situation au 7 avril

Sources

Ça sent vraiment mauvais en France…

Coefficients de corrélation (sans pondération) :

['morts (EHPAD\ncomprises) en France', 0.9986452551376457]
['COVID+ (EHPAD\ncomprises) en France', 0.998154880022019]
['morts en Espagne', 0.9997929741959563]
['COVID+  en Espagne', 0.9998977252219694]
['morts en Italie', 0.9998265190335354]
['COVID+ en Italie', 0.9997830570147496]
['morts en Allemagne', 0.9998391663051124]
['COVID+ en Allemagne', 0.9997505578976235]
['morts aux USA', 0.9997596098534672]
['COVID+ aux USA', 0.9997160845256463]
['morts au Royaume-Uni', 0.9976629910135661]
['COVID+ au Royaume-Uni', 0.9998716396081186]
['morts en AuvRhAl', 0.9997838014102479]
['COVID+ en AuvRhAl', 0.99958465387001]
['hospitalisations en France', 0.9997660961856307]

France

Monde

Situation au 8 avril

Sources

Coefficients de corrélation (avec pondération) :

['morts (EHPAD\ncomprises) en France', 0.9985955996418283]
['COVID+ (EHPAD\ncomprises) en France', 0.9982215805730525]
['morts en Espagne', 0.9998488110896219]
['COVID+  en Espagne', 0.9999093920168082]
['morts en Italie', 0.9999091956892686]
['COVID+ en Italie', 0.999823925653786]
['morts en Allemagne', 0.9995761000733545]
['COVID+ en Allemagne', 0.999814685511823]
['morts aux USA', 0.9997589684029945]
['COVID+ aux USA', 0.9999003363661323]
['morts au Royaume-Uni', 0.9986597488652262]
['COVID+ au Royaume-Uni', 0.9999286204532191]
['morts en AuvRhAl', 0.9997527867010059]
['COVID+ en AuvRhAl', 0.9997402816063816]
['hospitalisations en France', 0.9999321858316611]

France

Le sort des EHPAD dont je m’inquiétais le 4 avril devient une inquiétude partagée par d’autres. Les données du jour en France ne font pas apparaître la situation dans les EHPAD, pour lesquelles elles ne sont pas parvenues jusqu’au gouvernement. Mais, avec ou sans ces données, le satisfécit des médias concernant l’amélioration de la situation en France est une manière de plus de passer sous silence l’hécatombe qui est en train de s’y produire. Si les statistiques sur les hospitalisations poussent à l’optimisme, c’est précisément parce qu’elles ne tiennent aucun compte des ravages de l’épidémie en EHPAD dont les pensionnaires n’ont aucune perspective de soins en hôpitaux :

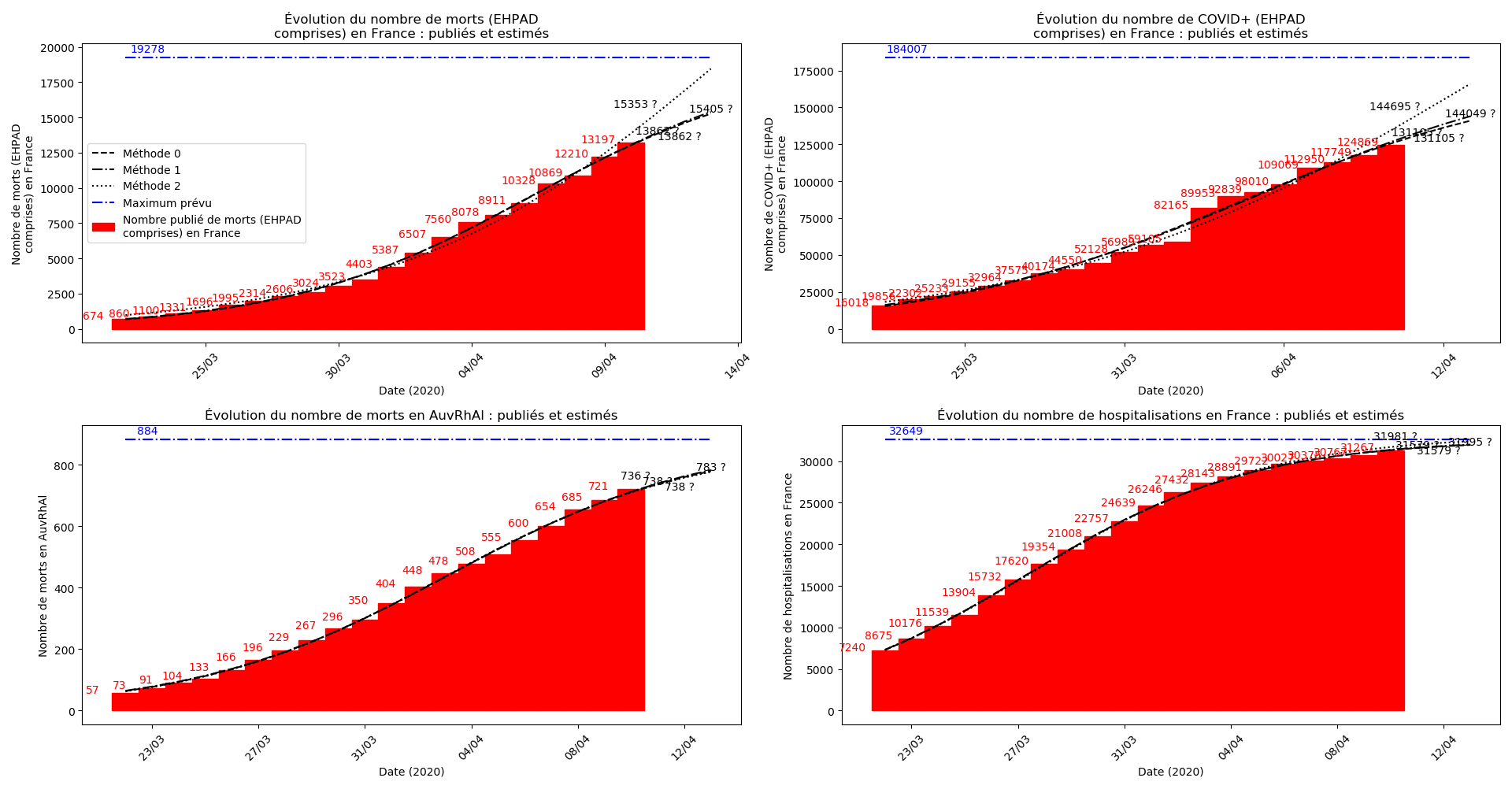
Dans ces circonstances, je commence à avoir peur que les prévisions alarmistes de la méthode 2 puissent correspondre à une réalité :

Les autres graphiques sont rendus en partie illisibles par les à-coups avec lesquels les remontées de la progression de l’épidémie en EHPAD arrivent :

Monde

Seules l’Espagne et l’Italie voient une réelle amélioration de la situation. En France, en Allemagne, aux USA, au Royaume-Uni, si les situations sont extrêmement différentes avec des politiques publiques extrêmement diverses avant et depuis l’épidémie de CoViD, cette dernière semble cependant en être au même point de sa progression :

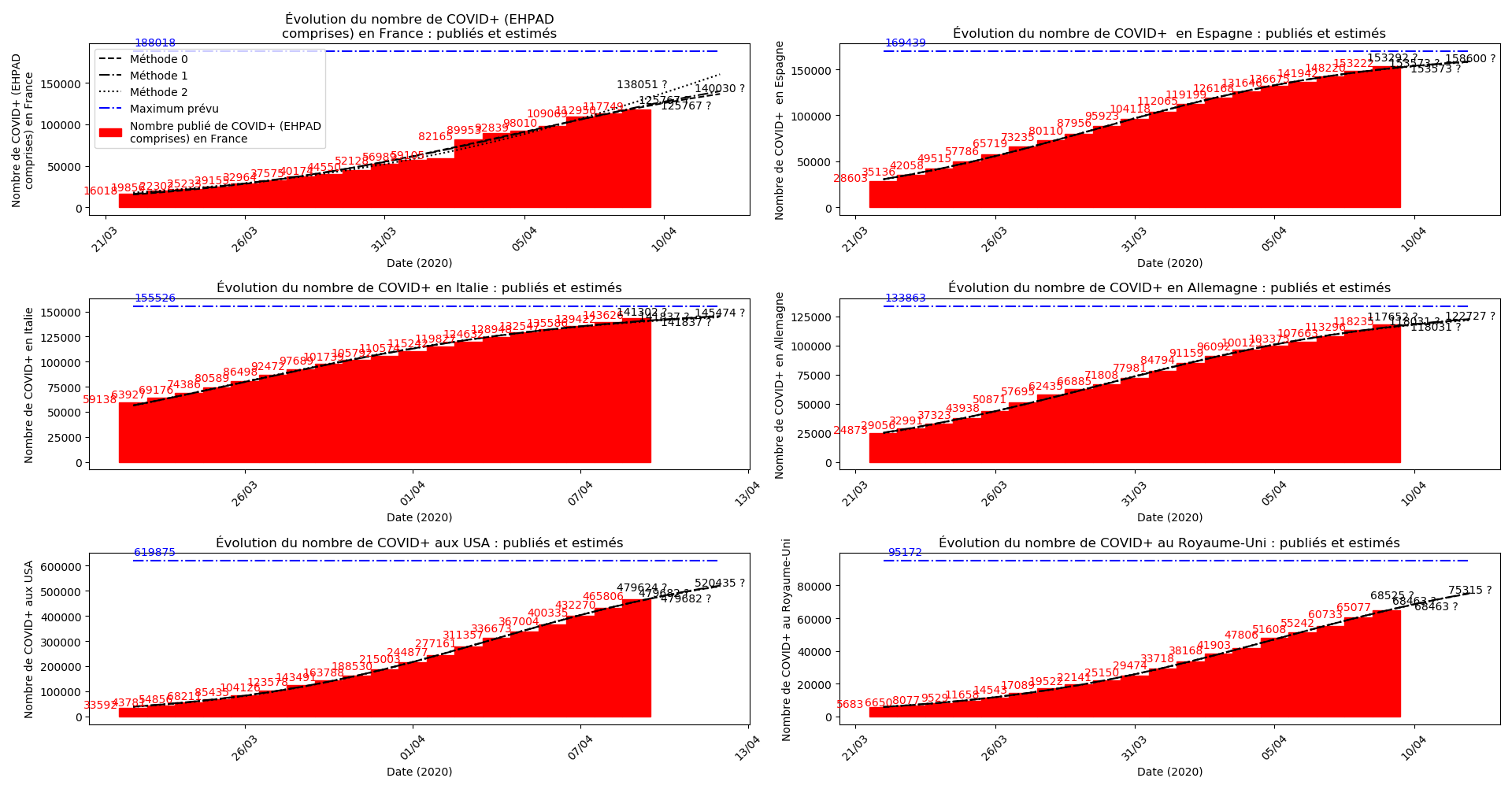
Concernant le nombre de CoViD+, les trois méthodes de simulation donnent des prévisions très cohérentes et groupées, sauf en France où les remontées alternatives des données des EHPAD engendrent des divergences :

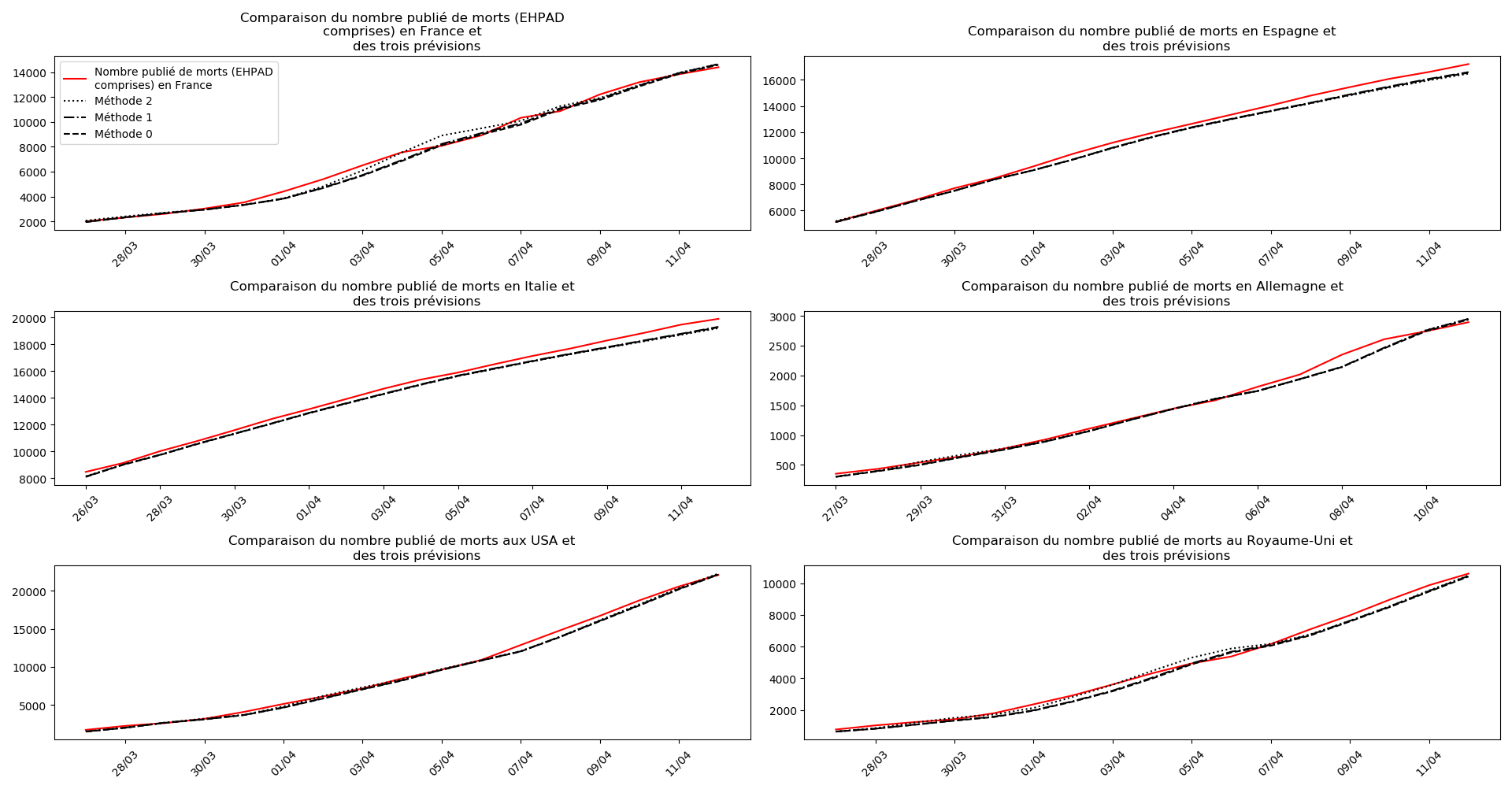
Concernant le nombre de décès, on retrouve les inquiétudes que je formulais plus haut pour la France, l’Allemagne, les USA et le Royaume-Uni.

Situation au 9 avril

Sources

France

Les données françaises jouent au yoyo. Véritables difficultés à faire remonter les informations ? Inaptitude et incompétence du gouvernement ? Les informations qui remontent quotidiennement de la progression de l’épidémie en France ressemblent à la trajectoire d’un bateau ivre ou à la course d’un chien fou. Dans ces conditions, l’interpolation des données ne peut être que de piètre qualité. Quelle tristesse d’affronter une telle crise avec aux commandes du pays un tel gouvernement de médiocres et de dissimulateurs…

Monde

Sur le plan purement algorithmique, la méthode 2 montrent à la fois sa capacité à anticiper les valeurs asymptotiques dans le cas général, mais aussi sa trop grande sensibilité aux variations erratiques : difficile d’accorder du crédit aux valeurs prévues du nombre de décès en fin d’épidémie pour la France et le Royaume-Uni. Tandis qu’au contraire, pour l’Espagne et l’Allemagne, les valeurs concordantes actuelles ont été prévues il y a plus de 10 jours.

Situation au 10 avril

Sources

France

Monde

Situation au 12 avril

Sources

J’ai à nouveau modifié la méthode 2.

Quelques remarques : les trois méthodes sous-estiment désormais (beaucoup) les données de l’Espagne et de l’Italie. Je n’en comprends pas vraiment la raison.

Les hospitalisations en France ont désormais passé le pic depuis longtemps. Le nombre de COVID+ passe à peine ce pic. Ce décalage temporel est l’inverse de celui que l’on attend. Il est incompréhensible à moins de considérer que les pensionnaires des EHPAD ne sont pas hospitalisés et que rien n’y a été fait pour enrayer la progression de l’épidémie.

France

Monde

Situation au 13 avril

Sources

France

Monde

Situation au 14 avril

Sources

France

Monde

Les prévisions du modèle en Espagne et en Italie sous-estiment énormément désormais les données réelles. Je ne sais pas trop si cela dit quelque chose de l’évolution de la situation dans ces deux pays ou si c’est le signe que le modèle n’est tout simplement pas valide. Notamment, les sigmoïdes ont un centre de symétrie qui n’a pas de justification à priori dans les données réelles d’épidémie.

Situation au 17 avril

Sources

Il devient patent que la modélisation par une sigmoïde n’est pas valide : l’épidémie s’éteint beaucoup trop lentement pour que ce soit le cas.

Par ailleurs, les données françaises sont ridiculement irrégulières : la situation dans les EHPAD a été cachée le plus longtemps possible par le gouvernement, elle lui explose à la tête. Ce sont au mieux des incapables, au pire des criminels.